
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Рядами динамики называют ряды, которые характеризуют изменение явления во времени
Рядами динамики называют ряды, которые характеризуют изменение явления во времени. Ряды динамики бывают моментные и интервальные. Моментные ряды характеризуют изменение явления в динамике на определенный момент времени (чаще — на начало или конец периода).
Интервальные ряды характеризуют изменение явления в динамике за определенный период времени (месяц, квартал, год).
В экономическом анализе используют аналитические показатели динамики. К ним относят абсолютный прирост, средний абсолютный прирост, темп роста, темп прироста, средний темп роста, абсолютное значение одного процента прироста. Данные показатели широко используются в статистической практике, что вызывает необходимость тщательного изучения методологии их расчета.
Рассмотрим на примере расчет аналитических показателей ряда динамики (табл. 7.1).
Таблица 7.1
| Месяцы | Выпуск цехом товарной продукции, тыс. руб. | Показатели динамики | |||||
| Абсолютный прирост, тыс. руб. (∆) | Темп роста, % (Тр) | Темп прироста, % (Тпр) | Абсолютное значение 1% прироста, тыс. руб. (А) | ||||
| цепной | базисный | цепной | базисный | ||||
| - | - 103,4 100,8 101,2 100,4 100,8 | 100,0 103,4 100,8 101,2 100,4 100,8 | - 3,4 0,8 1,2 0,4 0,8 | - 3,4 4,2 5,5 5,9 6,8 | - 2,4 2,5 2,5 2,5 2,5 |
Абсолютный прирост ∆ определяется как разность между отчетным и предыдущим уровнями ряда динамики, т. е. по формуле

где уi — уровни ряда динамики.
Абсолютный прирост характеризует абсолютное изменение явления в отчетном периоде по сравнению с предыдущим. Так, например, абсолютный прирост продукции цеха в феврале по сравнению с январем составил 244 - 236 = 8 тыс. руб., а в марте по сравнению с февралем 246 - 244 = 2 тыс. руб. и т. п.
Средний абсолютный прирост  определяется на основе данных абсолютных приростов по следующим формулам:
определяется на основе данных абсолютных приростов по следующим формулам:

где п — число уровней ряда динамики;
y1 и yn— соответственно первый и последний абсолютные уровни ряда динамики.
Средний абсолютный прирост за рассматриваемый период динамики составит:

или

То есть за рассматриваемый период прирост продукции в среднем составил 3,2 млн руб.
Темп роста Тр определяется по формуле:
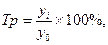
где y0 — уровень ряда динамики, взятый за базу сравнения.
Темп роста характеризует относительный рост явления за рассматриваемый период.
Темпы роста рассчитываются по принципу цепных и базисных соотношений. В том случае, когда за базу сравнения принимается предыдущий период, рассчитываются цепные показатели темпа роста; когда сравнение осуществляется с любым другим уровнем ряда динамики, взятым за базу сравнения, — рассчитываются базисные темпы роста.
Так, в феврале по сравнению с январем выпуск продукции в цехе составил Тр2 = (244 : 236) × 100% = 103,4%, а в марте по сравнению с февралем — Тр3 = (246 : 244) × 100,8% и т.д.
Если за базу сравнения взять январь, то выпуск продукции в цехе в марте по сравнению с январем составил (246 : 236") × 100% = 104,2%, а в апреле по сравнению с январем — (249 : 236) × 100% = 105,5% и т. д.
Темп прироста Тпр в отличие от темпа роста характеризует относительный прирост явления в отчетном периоде по сравнению с тем уровнем, с которым осуществляется сравнение, и определяется по формуле:
Тпр = Тр - 100%.
Так, в марте объем продукции цеха по сравнению с февралем увеличился на 0,8% (100,8 - 100), а по сравнению с январем — на 4,2% (104,2 - 100) и т. д.
Абсолютное значение одного процента прироста А характеризует абсолютный эквивалент одного процента прироста и определяется по формуле:

Так, в феврале абсолютное значение одного процента прироста составило (8 : 3,4) = 2,4 млн руб.; в марте — (2 : 0,8) = 2,5 млн руб. и т. д.
Средний темп роста (X) за период динамики определяют по формуле средней геометрической двояким способом — на основе данных цепных коэффициентов динамики либо на основе данных абсолютных уровней ряда динамики по формулам:

где k1 k2, ...kn — коэффициенты динамики по отношению к предыдущему периоду;
п — число коэффициентов динамики;
l — число абсолютных уровней ряда динамики;
x1 и хп — соответственно первый и последний абсолютные уровни ряда динамики.
Так, за первое полугодие средний годовой темп роста продукции в цехе составил:

или

Один из важнейших вопросов, возникающих при изучении рядов динамики, — это выявление тенденции развития экономического явления в динамике. Для этой цели применяются разнообразные статистические методы, в частности метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания.
Наиболее простым в использовании является метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Выявление тенденции осуществляется по новому укрупненному ряду динамики.
Другой метод — метод скользящей средней — заключается в замене первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня ряда с постепенным включением последующих уровней.
Наиболее совершенным методом выявления тенденции ряда динамики является метод аналитического выравнивания, который заключается в замене первоначальных уровней ряда новыми, найденными во времени t путем построения аналитического уравнения связи.
Рассмотрим на примере возможности применения каждого из методов выравнивания при выявлении тенденции ряда динамики.
Известны следующие данные выполнения программы участком «молдинги» прессового корпуса за отчетный год, млн руб. (табл. 7.2).
1. По методу укрупнения интервалов имеем новые укрупненные поквартальные уровни ряда динамики:
y1 = 18,6 + 17,3 + 18,9 = 54,8;
у2 = 18,2 + 17,9 + 19,1 = 55,2 и т. д.
Таблица 7.2
| Месяцы | Выпуск молдингов, млн руб. | Месяцы | Выпуск молдингов, млн руб. |
| Январь Февраль Март Апрель Май Июнь | 18,6 17,3 18,9 19,2 17,9 19,1 | Июль Август Сентябрь Октябрь Ноябрь Декабрь | 19,6 17,5 19,2 19,8 18,3 19,4 |
Выравненный ряд динамики примет вид:
54,8 55,2 56,3 57,5
То есть наблюдается четко выраженная тенденция увеличения выпуска молдингов цехом за отчетный год.
2. Употребляя те же данные, применим метод скользящей средней, используя семичленную скользящую среднюю. Тогда:


Выравненный с помощью семичленной скользящей средней ряд динамики примет вид:
18,5 18,4 18,6 18,7 18,8 19,0
Таким образом, подтверждается тенденция увеличения выпуска молдингов за отчетный год.
3. Для осуществления метода аналитического выравнивания построим вспомогательную таблицу (табл. 7.3).
Таблица 7.3
| Месяцы | Выпуск молдингов, млн руб. | t | t2 | ty | yt = 18,6 + 0,05t |
| I | 18,6 | -11 | -204,6 | 18,1 | |
| II | 17,3 | -9 | -155,7 | 18,2 | |
| III | 18,9 | -7 | -132,3 | 18,3 | |
| IV | 18,2 | -5 | -91,0 | 18,4 | |
| V | 17,9 | -3 | -53,7 | 18,5 | |
| VI | 19,1 | - 1 | -19,1 | 18,6 | |
| VII | 19,6 | + 1 | 19,6 | 18,7 | |
| VIII | 17,5 | + 3 | 52,5 | 18,8 | |
| IX | 19,2 | + 5 | 96,0 | 18,9 | |
| X | 19,8 | + 7 | 138,6 | 19,0 | |
| XI | 18,3 | + 9 | 164,7 | 19,1 | |
| XII | 19,4 | + 11 | 213,4 | 19,2 | |
| Итого: | 223,8 | 28,5 | 223,8 |

Используя метод отсчета от условного нуля, введем условное обозначение времени t, придав ему определенные значения так, чтобы 
Судя по выявленной с помощью двух предыдущих методов тенденции выпуска молдингов в течение года, можно сказать, что наиболее вероятна линейная зависимость данного распределения от времени t и данному распределению соответствует уравнение прямой:

Для нахождения параметров а0 и а1, используем систему уравнений:.

Поскольку 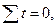 то имеем:
то имеем:


Следовательно, уравнение прямой примет вид  и будет в данном случае искомым, т. к.
и будет в данном случае искомым, т. к. 
Контрольные вопросы
1. Какие показатели динамики используются в экономическом анализе?
2. В чем отличие цепных от базисных показателей динамики?
3. В чем сущность метода укрупнения интервалов?
4. Как используется метод скользящей средней?
5. В чем сущность метода аналитического выравнивания?
Дата добавления: 2014-12-23; просмотров: 309; Мы поможем в написании вашей работы!; Нарушение авторских прав |