
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Наряду со средней величиной, характеризующей типичный уровень варьирующего признака, около которого колеблются отдельные значения признака
Наряду со средней величиной, характеризующей типичный уровень варьирующего признака, около которого колеблются отдельные значения признака, рассматривают показатели вариации (колеблемости) признака, позволяющие количественно измерить величину этой колеблемости.
К показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Простейшим показателем вариации является размах вариации, который рассчитывается по следующей формуле:

где Xmax, Xmin – соответственно максимальное и минимальное значение признака в исследуемой совокупности.
Размах вариации характеризует диапазон колебаний признака в изучаемой совокупности и измеряется в тех же единицах, в которых выражен признак.
Рассчитывают среднее линейное отклонение, которое бывает невзвешенное и взвешенное. Если каждое значение признака встречается в совокупности один раз, то применяется формула среднего линейного отклонения невзвешенного.

где х — значения признака;
 — среднее значение по совокупности;
— среднее значение по совокупности;
п — количество значений.
Если имеется некоторая повторяемость значений признака, то применяется формула среднего линейного отклонения взвешенного:
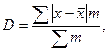
где т — частота.
Среднее линейное отклонение характеризует абсолютный размер колеблемости признака около средней и измеряется в тех же единицах, в которых выражен признак.
Наиболее точным показателем вариации является среднее квадратическое отклонение. Для его определения предварительно рассчитывают показатель дисперсии. Дисперсия невзвешенная определяется по формуле:

Дисперсия взвешенная определяется по формуле:
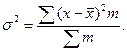
Тогда, соответственно, для расчета среднего квадратического отклонения невзвешенного используют формулу:
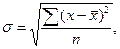
а для расчета среднего квадратического отклонения взвешенного — следующую формулу:

Как и среднее линейное отклонение, среднее квадратическое отклонение характеризует абсолютный размер колеблемости признака около средней, однако является более точной характеристикой.
В статистическом анализе в расчетах можно одновременно использовать показатели среднего линейного и среднего квадратического отклонения, а экономические выводы делать в пределах вариации значений обоих показателей.
В отличие от среднего линейного и среднего квадратического отклонения, коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности. Он определяется по формулам:

Если коэффициент вариации ≥ 33,3%, исследуемая совокупность считается весьма неоднородной и не может быть подвергнута дальнейшему исследованию. Ее следует разгруппировать.
Если исследуемую совокупность единиц расчленить на группы, то можно считать, что общая дисперсия всей совокупности варьирует (изменяется) под влиянием дисперсий для каждой отдельной группы, так называемых групповых или частных дисперсий и межгрупповой дисперсии. Эти дисперсии связаны между собой правилом сложения дисперсий. При использовании правила сложения дисперсий в экономическом анализе по величине частной дисперсии может решаться задача выявления наиболее эффективной в производстве системы (формы, структуры и т. п.) организации труда, его оплаты и т. п.
Частные или групповые дисперсии характеризуют колеблемость изучаемого признака в каждой отдельной группе и определяются по следующей формуле:

где х — значения признака;
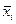 — средняя по совокупности в i-той группе;
— средняя по совокупности в i-той группе;
mi — численность единиц в i-той группе;
i = 1, 2, ...п — номер группы.
Средняя из частных дисперсий определяется по формуле:
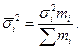
Межгрупповая дисперсия характеризует колеблемость частных средних 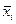 около общей средней
около общей средней  и определяется следующим образом:
и определяется следующим образом:

Отдельно рассчитывается общая дисперсия σ2 по формуле:

При соблюдении правила сложения дисперсий должно соблюдаться равенство:
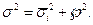
1. Проиллюстрируем расчет показателей вариации по данным о распределении рабочих по стажу работы (табл. 6.1).
Таблица 6.1
| Стаж работы рабочего, лет (х) | Число рабочих, чел. (т) | хт | 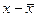
| 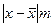
| 
| 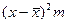
|
| -1,4 -0,4 0,6 1,6 2,6 | 19,6 4,4 4,8 9,6 10,4 | 1,96 0,16 0,36 2,56 6,76 | 27,44 1,76 2,88 15,36 24,04 | |||
| Итого: | — | 48,8 | 11,80 | 74,48 |

т. е. диапазон колебания рабочих по стажу работы в исследуемой совокупности составляет 4 года.

т. е. средний стаж рабочих по совокупности составляет 11,4 года.
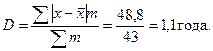
В среднем на 1,1 года отклоняется стаж отдельных рабочих от среднего стажа по совокупности.
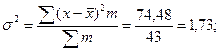
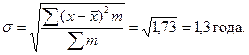
Величина σ = 1,3 года характеризует колеблемость стажа рабочих в данной совокупности:

Таким образом, на 11,4% варьирует состав рабочих по стажу работы в исследуемой совокупности.
2. Используя правило сложения дисперсий, определим наиболее эффективную систему оплаты труда рабочих по следующим данным (табл. 6.2).
3. Рассчитаем частные дисперсии по формуле:

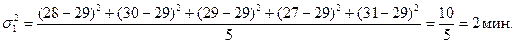
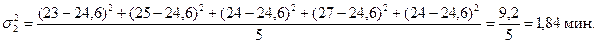

Таблица 6.2
| Системы оплаты труда | Затраты времени на производимыеоперации, мин. (х) | Число рабочих, чел. (m) | Всего затрачено времени, мин. (∑x) | Затраты времени в среднем, мин. (х) |
| Простая сдельная | 28, 30, 29, 27, 31 | 29,0 | ||
| Сдельная премиальная | 23, 25, 24, 27, 24 | 24,6 | ||
| Сдельная прогрессивная | 18, 16, 19, 21, 20 | 18,8 | ||
| Итого: | 24,13 |
Рассчитаем среднюю из частных дисперсий по формуле:

Определим межгрупповую дисперсию по формуле:

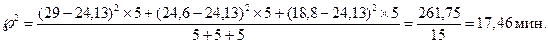
Определим общую дисперсию по формуле:
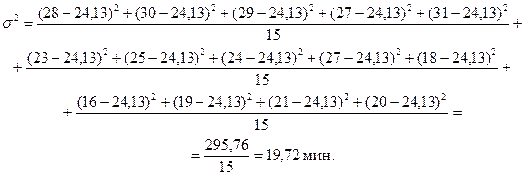
Так как соблюдается правило сложения дисперсий, а именно: 19,72 = 17,46 + 2,26, то можно считать по максимальной величине частной дисперсии 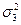 =2,96 мин., что наиболее эффективной системой оплаты труда по исследуемой совокупности является сдельная прогрессивная оплата труда.
=2,96 мин., что наиболее эффективной системой оплаты труда по исследуемой совокупности является сдельная прогрессивная оплата труда.
Контрольные вопросы
1. Каковы экономический смысл и методология расчета показателя размаха вариации?
2. Каковы назначение и методология расчета среднего линейного отклонения и среднего квадратического отклонения?
3. В каком случае применяются невзвешенные и взвешенные показатели вариации?
4. Какова экономическая интерпретация коэффициента вариации?
5. В чем заключается правило сложения дисперсий и каково его экономическое назначение?
Тема 7. РЯДЫ ДИНАМИКИ
Основные теоретические вопросы
Понятие ряда динамики.
Виды рядов динамики.
Моментные и интервальные ряды динамики.
Показатели ряда динамики.
Средний уровень ряда и способы его вычисления.
Абсолютный прирост.
Средний абсолютный прирост.
Темпы роста и прироста.
Средний темп роста.
Абсолютное значение одного процента прироста.
Цепные и базисные показатели динамики.
Методы выявления тенденции ряда динамики.
Метод укрупнения интервалов.
Метод скользящей средней.
Аналитическое сглаживание рядов динамики.
Дата добавления: 2014-12-23; просмотров: 1098; Мы поможем в написании вашей работы!; Нарушение авторских прав |