
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Средние величины в статистике выполняют роль обобщающих показателей, характеризующих изучаемую совокупность единиц по какому-либо признаку.
Средние величины в статистике выполняют роль обобщающих показателей, характеризующих изучаемую совокупность единиц по какому-либо признаку.
При изучении вопроса о применении средних особое внимание следует обратить на то, что каждый вид средней определяется в зависимости от конкретного экономического условия и от поставленной задачи. В противном случае средняя даст ошибочный результат и будет являться искаженной характеристикой изучаемой статистической совокупности.
Следует уяснить, что средняя рассчитывается по качественно однородной совокупности, значения которой примерно одного порядка. Это основное условие применения средней.
Следует знать, что средние величины в статистике являются величинами именованными и выражаются в тех же единицах, в которых выражен признак.
В статистическом анализе используют следующие виды средних величин:
• средняя арифметическая простая,
• средняя арифметическая взвешенная,
• средняя гармоническая,
• средняя геометрическая,
• структурные средние: медиана и мода.
1. Средняя арифметическая простая применяется в том случае, когда каждая единица совокупности имеет свое конкретное значение.
Средняя арифметическая простая рассчитывается по формуле:

где X — значение показателя;
п — число значений.
Рассчитаем среднюю арифметическую простую по следующим данным:
| Порядковый номер рабочих | |||||||
| Количество изготовленных деталей, тыс. шт. | 1,0 | 1,1 | 1,0 | 0,9 | 1,2 | 1,1 | 1,0 |
В данном случае применима средняя арифметическая простая:

Таким образом, средняя выработка деталей на одного рабочего составляет 1,0 тыс. шт.
2. Средняя арифметическая взвешенная применяется в том случае, когда имеется некоторая повторяемость значений единиц совокупности. Средняя арифметическая взвешенная рассчитывается по формуле:

где т — частота (повторяемость признака).
По данным о распределении рабочих-наладчиков по стажу работы и квалификации участка одного из цехов промышленного предприятия рассчитаем среднюю арифметическую взвешенную (табл. 5.1).
Определить:
а) средний разряд рабочих каждой возрастной группы,
б) средний стаж рабочих участка.
Таблица 5.1
| Стаж работы, лет | Число рабочих, чел. | |||
| всего | в том числе имеющих разряд | |||
| IV | V | VI | ||
| до 10 | ||||
| 10—20 | - | |||
| 20—30 | - | |||
| 30—40 | - | - |
Решение:
а) для нахождения среднего разряда рабочих каждой возрастной группы следует применить среднюю арифметическую взвешенную: в качестве веса (m) выступает конкретный разряд рабочих. Так, для рабочих со стажем работы до 10 лет средний тарифный разряд составит:

Для рабочих со стажем работы 10—20 лет средний тарифный разряд составит

И так далее по другим возрастным группам;
б) для нахождения среднего стажа рабочих на участке применяют ту же среднюю арифметическую взвешенную, но уже для интервального ряда распределения:

Причем в качестве х будут средние значения признака в группах, а в качестве веса т принимают численность рабочих соответствующей группы:

Таким образом, средний стаж рабочих по совокупности — 14 лет. Можно также рассчитывать средний стаж рабочих по соответствующим квалификационным группам. Так, для рабочих 5-го разряда средний стаж составит:

Аналогичные расчеты можно произвести по другим квалификационным группам.
3. Средняя гармоническая применяется в том случае, когда известен один из сомножителей и само произведение.
Средняя гармоническая определяется по формуле:

где X — известный сомножитель;
М — известное произведение.
Например, требуется вычислить средний процент выполнения плана по выпуску продукции цехом, состоящим из четырех участков (табл. 5.2).
Применение средней арифметической простой исключается, т. к. процентные соотношения не подвергаются суммированию. Для решения данной задачи следует применить формулу средней гармонической. Критерием правильности применения данной формулы является то, что числитель ∑М представляет собой суммарный объем выпуска продукции участками цеха, а знаменатель  - суммарную величину выпуска продукции по плану.
- суммарную величину выпуска продукции по плану.
Таблица 5.2
| Участки цеха | Фактически выпушено продукции, тыс. руб. | Процент выполнения плана |
| Токарный | 101,3 | |
| Фрезерный | 90,5 | |
| Расточный | 102,5 | |
| Слесарный | 101,9 |
Подставляя числовые данные в формулу, получаем:

Таким образом, средний процент выполнения плана по выпуску продукции цехом составил 98,4%.
4. Средняя геометрическая используется для определения среднего темпа роста явления за рассматриваемый период динамики. Средняя геометрическая рассчитывается двояко:

или

где k1 k2, ...kn —коэффициенты динамики по отношению к предыдущему периоду;
п —число коэффициентов динамики;
x1 и x2 —соответственно первый и последний абсолютные уровня и ряда динамики;
l —число абсолютных уровней ряда динамики.
Требуется определить средний темп роста выпуска литья в оболочковых формах в литейном цехе завода за пятилетний период по данным (табл. 5.3).
Произведем расчет:

или

Таблица 5.3
| Годы | 1-й | 2-й | 3-й | 4-й | 5-й |
| Выпуск литья, тонн | 230,1 | 243,8 | 261,5 | 285,8 | 286,6 |
| В % к предыдущему году | — | 105,9 | 107,3 | 109,3 | 100,3 |
Таким образом, средний темп роста выпуска литья составил 105,6%.
Для изучения структуры исследуемой совокупности применяют так называемые структурные средние: медиану и моду.
5. Медианой в статистике называют такое значение признака, которое расположено в середине упорядоченного ряда. Медиана определяется по-разному для дискретного и интервального вариационных рядов.
Медиана дискретного вариационного ряда, расположенного в ранжированном порядке, имеет серединное значение.
Медиана в интервальном вариационном ряде определяется по формуле:
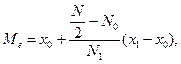
где х0 и х1 — соответственно нижняя и верхняя границы медианного интервала;
N — сумма частот ряда;
N0 — сумма частот, накопившаяся до начала медианного интервала;
N1, — частота медианного интервала.
По следующим данным дискретного ряда распределения, расположенного в ранжированном порядке (в порядке возрастания), определим медиану:
| Номер по порядку рабочего | |||||
| Стаж работы, лет |
Так как медиана имеет значение признака, находящееся в середине упорядоченного ряда, то для данного ряда распределения медиана составит 9 лет. Это значит, что половина совокупности рабочих имеет стаж работы до 9 лет, половина — более 9 лет.
Несколько сложнее определяется медиана для интервального вариационного ряда (табл. 5.4).
Прежде всего находится медианный интервал, на который должно приходиться 50% накопленных частот данного ряда, что по условию задачи: 40 : 2 - 20. Сумма частот первых двух интервалов равна 19, что меньше 20. Следовательно, медианный интервал будет находиться не во второй группе, а в третьей, т. е. в пределах границ 105—110.
Таблица 5.4
| Выполнение месячного задания, % | Число рабочих, чел. | Накопленные частоты от начала ряда |
| 95—100 | ||
| 100—105 | ||
| 105—110 | ||
| 110—115 | ||
| 115—120 |
Подставим соответствующие значения в формулу:

Таким образом, 50% всех рабочих выполняют производственное задание менее чем на 105,6%, 50% — более чем на 105,6%.
6. Модой в статистике называют наиболее часто встречающееся в исследуемой совокупности значение признака.
В дискретном вариационном ряде моду определяют по наибольшей частоте. В интервальном вариационном ряде мода определяется по формуле:

где x0 и x1 — соответственно нижняя и верхняя границы модального интервала;
f2 — частота модального интервала;
f1 и f3 — частота интервала соответственно предшествующего и следующего за модальным.
По следующим данным дискретного ряда распределения определим моду:
| Дневная выработка рабочего, шт. | ||||||
| Число рабочих, имеющих данную выработку, чел. |
Просматривая частоты ряда (число рабочих), видим, что наибольшая частота — 12. Эта частота соответствует дневной выработке 20 шт. Таким образом, мода показывает, что в данной совокупности наибольшее число рабочих имеют выработку 20 шт. деталей в день.
Несколько иначе определяется мода для интервального вариационного ряда. В качестве примера возьмем условие задачи из таблицы 5.4.
Прежде всего находится модальный интервал, на который должна приходиться наибольшая частота, по условию задачи в табл. 5.4 это будет интервал 100—105, так как ему соответствует наибольшая частота — 16 чел. Подставим соответствующие значения в формулу:

Иначе говоря, наибольшее число рабочих выполняют месячное задание на 103%.
Контрольные вопросы
1.Какова экономическая сущность средней?
2.Какие формы средней рассчитываются в экономических исследованиях?
3.Какова методология расчета средней по данным интервального вариационного ряда?
4.Каковы экономический смысл и методология расчета структурных средних?
Какой интервал в интервальном вариационном ряде называется модальным, какой медианным?
Дата добавления: 2014-12-23; просмотров: 365; Мы поможем в написании вашей работы!; Нарушение авторских прав |