
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. При изучении взаимосвязей между экономическими явлениями выделяют факторные и результативные признаки
При изучении взаимосвязей между экономическими явлениями выделяют факторные и результативные признаки. Факторным признаком является тот, который влияет и обуславливает изменение результативного признака. Результативный признак — тот, который изменяется под влиянием факторного признака.
Различают два вида взаимосвязей экономических явлений: функциональные и корреляционные.
При функциональных связях каждому значению факторного признака соответствует вполне определенное значение результативного признака. Функциональные связи можно формализовать, т. е. представить в виде формулы. Например, в функциональной связи находится объем выпуска продукции от двух факторов сомножителей: средней выработки продукции на одного рабочего и средней списочной численности рабочих.
При функциональных связях применяется индексный метод анализа.
При корреляционных связях отдельным значениям факторного признака может соответствовать несколько значений результативного признака. Корреляционная связь проявляется в среднем при большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и факторным признаком. В корреляционной зависимости находится, например, объем выпуска продукции от ряда факторов: уровня механовооруженности труда, коэффициента сменности, квалификации рабочих и т. п. В данном случае построить функцию зависимости результативного признака от факторного без применения специального математического аппарата не представляется возможным.
При корреляционных связях применяется корреляционный метод анализа.
Связи между явлениями бывают прямые и обратные. При прямых связях с увеличением (уменьшением) факторного признака результативный увеличивается (уменьшается).
В прямой зависимости находится, например, объем выпуска продукции от производительности труда или коэффициента сменности. При обратных связях с увеличением (уменьшением) факторного признака результативный уменьшается (увеличивается). В обратной зависимости находится, например, объем выпуска продукции от величины простоев оборудования, от текучести рабочих кадров и т. п.
По аналитическому выражению связи бывают прямолинейные и криволинейные. Прямолинейные связи выражают уравнением прямой. Криволинейные связи выражают уравнением параболы или гиперболы.
Особую трудность для усвоения представляет корреляционный метод анализа. Корреляционный метод анализа взаимосвязи экономических явлений проводят в три этапа. На первом этапе осуществляется выбор формы связи между факторным и результативным признаками, т. е. выбирается тип аналитической функции.
На втором этапе осуществляется решение аналитического уравнения связи путем нахождения его параметров.
На третьем этапе определяется теснота связи между изучаемыми экономическими явлениями.
Прежде чем подробно остановиться на каждом из трех этапов корреляционного анализа, обратим внимание на следующее.
В том случае, когда определяется влияние одного фактора на результативный признак, строится однофакторная регрессионная модель (парное уравнение корреляции); когда определяется влияние двух и более факторов на результативный признак — строится многофакторная регрессионная модель (уравнение множественной корреляции).
При подборе факторов для регрессионной модели следует помнить, что факторы не должны находиться в функциональной связи с результативным признаком. В противном случае должен применяться индексный метод анализа, а не корреляционный. Следует также знать, что число наблюдений для построения однофакторной регрессионной модели должно быть не менее 10—12.
Первый этап корреляционного анализа.
Для определения формы связи между факторным и результативным признакам, т. е. для установления типа аналитической функции связи, применяют различные статистические методы. Так, характер и направление связи между изучаемыми экономическими явлениями можно установить, применяя метод статистических группировок. С помощью данного метода наличие связи между явлениями устанавливается визуально.
Для выявления тенденции изменения результативного признака при изменении факторного могут использоваться такие статистические методы, как метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания. Чаще всего для установления формы зависимости между факторным и результативным признаками применяют графический метод.
При прямолинейной форме зависимости между факторным и результативным признаками функция связи имеет вид прямой:  ; при параболической форме — имеет вид параболы:
; при параболической форме — имеет вид параболы:  ; при гиперболической форме — вид гиперболы:
; при гиперболической форме — вид гиперболы: 
На втором этапе корреляционного анализа осуществляют решение аналитического уравнения связи путем нахождения его параметров a0, a1, ….. an.
Параметр a0 означает влияние на результативный признак не включенных в регрессионную модель факторов. Как правило, экономической интерпретации параметр a0 не подлежит. Параметры a0, a1, ….. an — коэффициенты регрессии, означают величину результативного признака при изменении факторного признака на единицу измерения.
В случае прямолинейной формы зависимости параметры аналитического уравнения связи  находятся путем решения следующей системы уравнений:
находятся путем решения следующей системы уравнений:

В случае параболической формы зависимости параметры аналитического уравнения связи  находятся путем решения следующей системы уравнений:
находятся путем решения следующей системы уравнений:
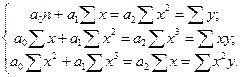
В случае гиперболической формы зависимости параметры аналитического уравнения связи  находятся путем решения следующей системы уравнений:
находятся путем решения следующей системы уравнений:

Для экономической интерпретации аналитического уравнения связи можно воспользоваться также коэффициентом эластичности, который рассчитывается по формуле:

Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак при изменении факторного на 1 процент.
На третьем этапе корреляционного анализа осуществляют оценку тесноты связи между факторным и результативным признаками с помощью показателей тесноты связи.
В случае линейной связи между факторным и результативным признаками производят расчеты линейного коэффициента корреляции по следующей формуле:

Линейный коэффициент корреляции варьирует в пределах от -1 до +1. Положительное его значение говорит о прямой связи, отрицательное — об обратной. Близость к нулю говорит о слабой связи, близость к ± 1 говорит о существенной связи, при r = ± 1 — связь функциональная.
Для экономической интерпретации линейного коэффициента корреляции применяется коэффициент детерминации. Он определяется по формуле:

Коэффициент детерминации характеризует долю дисперсии результативного признака, объясняемую влиянием соответствующего факторного признака.
В случае криволинейной зависимости (параболической, гиперболической) тесноту связи между факторным и результативным признаками определяют с помощью корреляционного отношения по формуле:

Рассмотрим на конкретном примере применение корреляционного метода в изучении взаимосвязи экономических явлений.
Пример. По данным таблицы 10.1 построить аналитическое уравнение связи и определить тесноту связи между явлениями.
Таблица 10.1
| № п/п рабочих | ||||||||||||
| Разряд (у) | ||||||||||||
| Стаж работы, лет (x) |
Определим форму зависимости разряда рабочих от стажа их работы на предприятии, используя графический метод (рис. 10.1).

Судя по распределению, зависимость прямолинейная.
Как известно, прямолинейная зависимость подчиняется уравнению прямой:  .
.
Следовательно, параметры данного уравнения связи находятся путем решения следующей системы уравнений:

Для решения системы построим вспомогательную таблицу 10.2.
Таблица 10.2
| Стаж*; лет (x) | Разряд (у) | ху | x2 | y2 | 
|
| 2,4 | |||||
| 3,1 | |||||
| 3,1 | |||||
| 3,4 | |||||
| 4,1 | |||||
| 4,3 | |||||
| 4,6 | |||||
| 5,0 | |||||
| 5,1 | |||||
| 5,2 | |||||
| 6,3 | |||||
| Итого: 197 |
* В ранжированном порядке (в порядке возрастания значений х).
На основе данных таблицы 10.2 имеем систему уравнений в следующем виде:

Решим систему сравнений:



Следовательно, найденное аналитическое уравнение связи имеет вид:  . Подставим соответствующие значения х в уравнение и найдем новые значения
. Подставим соответствующие значения х в уравнение и найдем новые значения  .
.
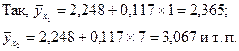
Изобразим по найденным значениям  теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии (см. рис. 10.1).
теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии (см. рис. 10.1).
Так как 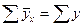 ,то можно считать, что построенное парное уравнение корреляции является искомым, и мы вправе сделать следующий вывод: с увеличением стажа работы на один год разряд рабочих в среднем возрастает на 0,117.
,то можно считать, что построенное парное уравнение корреляции является искомым, и мы вправе сделать следующий вывод: с увеличением стажа работы на один год разряд рабочих в среднем возрастает на 0,117.
Как было ранее сказано, экономическая интерпретация аналитического уравнения связи может осуществляться с помощью коэффициента эластичности. Расчетная величина коэффициента эластичности:

Таким образом, увеличение стажа работы на 1 процент приводит к увеличению разряда на 0,456 процента.
Как было сказано ранее, для установления тесноты связи между факторным и результативным признаками в случае линейной зависимости применяется линейный коэффициент корреляции.
Рассчитываем величину линейного коэффициента корреляции:


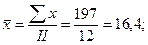
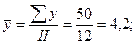



Как видно, связь между разрядом рабочего и стажем его работы на предприятии достаточно значительная, так как r = 0,77 близко к «1».
Для установления размера вариации разряда рабочего от стажа его работы рассчитываем коэффициент детерминации:

Следовательно, на 59,3% вариация разряда рабочего объясняется изменением стажа его работы на предприятии.
Анализ взаимосвязи между явлениями можно также проводить по сгруппированным данным, представленным в виде корреляционной таблицы. Приведем пример корреляционной таблицы, характеризующей связь между стажем рабочих и их заработной платой (табл. 10.3).
Таблица 10.3
| Стаж работы, лет (х) | Заработная плата, тыс. руб. | Итого | ||||||
| 40—50 | 50—60 | 60—70 | 70—80 | 80—90 | 90—100 | 100—110 | ||
| 0—5 | ||||||||
| 5—10 | ||||||||
| 10—15 | ||||||||
| 15—20 | ||||||||
| 20—25 | ||||||||
| 25—30 | ||||||||
| Итого ny: |
Корреляционная таблица показывает, что частоты (численность) рабочих концентрируются главным образом у диагонали. Это значит, что связь между стажем рабочего и его заработной платой прямая, то есть с увеличением стажа заработная плата рабочего возрастает. Характер линейной зависимости более четко прослеживается на графике (рис. 10.2). Для построения эмпирической линии регрессии рассчитаны средние показатели заработной платы по каждой из шести групп рабочих, выделенных по стажу работы:

Аналогично рассчитаны средние показатели заработной платы по другим группам рабочих. Результаты расчетов следующие:  ;
;  ;
;  ;
; 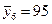 .
.
Как видно из рис. 10.2, очевидна прямолинейность зависимости заработной платы рабочих от стажа работы на предприятии. Такую зависимость можно выразить уравнением прямой:  .
.

Для построения уравнения зависимости, то есть нахождения его параметров а0 и a1 необходимо решить систему нормальных уравнений с использованием метода наименьших квадратов:

Для этого построим вспомогательную таблицу для х (табл. 10.4).
Таблица 10.4
| x | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 | Итого |
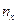
| |||||||

| 87,5 | 187,5 | 212,5 | 192,5 | 157,5 | 137,5 | |

| 218,7 | 1406,3 | 2656,3 | 3368,8 | 3543,8 | 3781,3 | 14 975,2 |
В таблице 10.4 в качестве х берутся средние значения х в интервалах группировки:  ;
;  и т. д. Умножая найденные групповые средние х на численность каждой группы пх получим хпх в пределах данной группы. Суммируя полученные величины по группам, получим общую
и т. д. Умножая найденные групповые средние х на численность каждой группы пх получим хпх в пределах данной группы. Суммируя полученные величины по группам, получим общую  , которая и будет выступать в качестве ∑x в решении системы уравнений.
, которая и будет выступать в качестве ∑x в решении системы уравнений.
Суммируя величины х2пх по группам, получим общую ∑х2пх =14975,2. Эта суммарная величина будет выступать в качестве ∑х2 для решения системы уравнений.
Построим вспомогательную таблицу для у (табл. 10.5). В таблице 10.5 в качестве у берутся средние значения у в интервалах группировки, а именно: 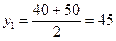 ;
;  и т. д. Умножая найденные групповые средние у на численность каждой группы пy , получим упу в пределах данной группы. Суммируя полученные величины по группам, получим общую ∑yny =7600. Эта суммарная величина и будет выступать в качестве ∑у в решении системы уравнений.
и т. д. Умножая найденные групповые средние у на численность каждой группы пy , получим упу в пределах данной группы. Суммируя полученные величины по группам, получим общую ∑yny =7600. Эта суммарная величина и будет выступать в качестве ∑у в решении системы уравнений.
Таблица 10.5
| y | Итого | |||||||
| ny У | ||||||||
| ynv | ||||||||
| y2ny | ||||||||
| пху | 562,5 | 14812,5 | 29212,5 | 7612,5 |
Несколько сложнее с ∑ху. Но если интервалы группировки малы, то можно считать значения х для всех единиц в рамках группы одинаковыми. Умножив средние значения х в интервалах группировки на соответствующие средние значения у и на численность данной группы, получим пху в пределах данной группы. Так, по данным табл. 10.3: 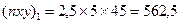 ;
;  и т.д. Сумма полученных значений по группам дает общую величину ∑xy=78525.
и т.д. Сумма полученных значений по группам дает общую величину ∑xy=78525.
Подставим найденные значения в систему уравнений и решим ее:






Следовательно, аналитическое уравнение связи заработной платы рабочих и стажа их работы имеет вид:  . На основе данного уравнения связи можно сделать вывод: с увеличением стажа работы на 1 год заработная плата рабочего увеличивается на 1,05 тыс. руб.
. На основе данного уравнения связи можно сделать вывод: с увеличением стажа работы на 1 год заработная плата рабочего увеличивается на 1,05 тыс. руб.
Рассчитаем тесноту связи между х и у с помощью линейного коэффициента корреляции:



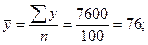

Таким образом, заработная плата рабочих на 39,6% зависит от стажа их работы на предприятии.
Контрольные вопросы
1.Какие различают два вида взаимосвязей экономических явлений?
2.Какие выделяют связи по направлению и в чем их сущность?
3.Какие существуют методы изучения взаимосвязи экономических явлений?
4.В чем сущность корреляционного метода анализа?
5.Что характеризуют линейный коэффициент корреляции и корреляционное отношение; каково их применение?
6.Каковы особенности проведения корреляционного анализа по сгруппированным данным?
Дата добавления: 2014-12-23; просмотров: 1797; Мы поможем в написании вашей работы!; Нарушение авторских прав |