
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 8. Показатели вариации
Среднее линейное отклонение – на сколько в среднем отлича
индивидуальные знач признака от ср его знач.
-для несгруппированных данных
(первичного ряда): 
-для вариационного ряда: 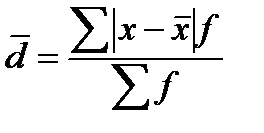
Среднее квадратическое отклонение
- для несгруппированных данных: 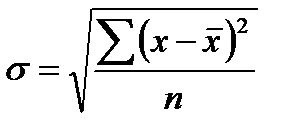
- для вариационного ряда: 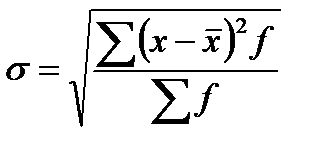
Дисперсия
- для несгруппированных данных: 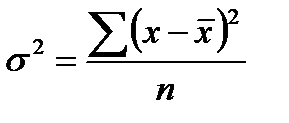
- для вариац-го ряда: 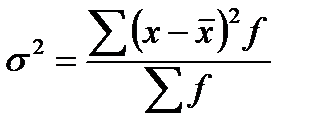
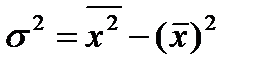
Коэффициент вариации (использ для характ однородности
совокуппо исследуемому признаку)
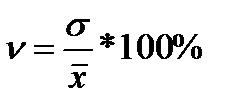 до 17% – совок совершенно однор,
до 17% – совок совершенно однор,
17%-33% - достаточно однородна, >33% - неоднородна.
8.14. На основ выписки, рассчит: размах вариации, среденее лин.отклон,
дисперсию, ср.квадратич отклон.,коэф.вариации.
| ФИО | З/п,тыс.руб. | ФИО | З/п,тыс.руб |
| Абрамов | Дронова | ||
| Аваньев | Дьякова | ||
| Бирюков | Евдокимов | ||
| Боброва | Кадырзанова | ||
| Бровкин | Мартынюк | ||
| Викулов | Мошкина | ||
| Ворошиолов | Нефедов | ||
| Гиршин | Прохина | ||
| Гудкой | Внукова |
Решение.
1)R=Xmax – Xmin = 35-10=25
2)Xср = ∑xi/n = 360/18=20
Среднее лин.отклон. Lср = ∑(Xi – Xср) / n = 0+7+6+5+3+..+15+1+6+0+6+10 / 18
3)σ2 = ∑(Xi – Xcp)2 / n = 49+36+25+9+64+49+4+49+100+9+225+1+36+36+100 / 18
4)σ= √σ2= 6,46
5)Vσ= σ/Xcp * 100% = 6,46/20 *100% = 32,3%
8.17. Для опред нормы затрат времени на выполнение 1банковской опер было
проведено обслед, результ кот представл ниже.
| Время,затрач на 1 банк.операцию,мин. | Число оперций |
| До 22 | |
| 22-24 | |
| 24-26 | |
| 26-28 | |
| 28-30 | |
| 30-32 | |
| 32 и выше |
Вычислите абсолютные и относительные(%) показатели вариации.
1)Xcp = ∑Xi*fi / ∑fi = 21*6+23*13+25*22...+33*6 / 6+13+22+36+10+7+6
R=Xmax – Xmin =34-20=14 Dвзв ср = ∑│Xi - Xcp│*fi / ∑fi = (21-26,52)*6….
Итд.=5,52*6+3,52*13+1,52*22+…+1,48*6 / 100 = 224,64/100 = 2,2464
σ2 = ∑(Xi – Xcp)2 *fi / ∑fi = 182,8224+161,0752+50,8288 +8,2944+61,504+
140,4928+251,9424 / 100 = 856,96 / 100 = 8,5696
σ=√σ2=2,93
VR= R/Xcp *100% = 14/26,52 *100% = 52,79%
Vdcp=dcp/Xcp *100% = 2,2464/26,52 *100% = 8,5%
Vσ= σ/Xcp *100% = 11% => <33% (см теор)
Совокупность по данному признаку можно считать однородной.
8.22. Вычислите дисперсию, еслиизвестно, что средняя величина признака
составляет 150 руб.,а коэф вариации = 15%.
Vσ= σ/Xcp *100%
σ2= (Xcp*Vσ / 100%)2= (150*0,15)2= 506,25
8.23. Ср.квадрат индивидуальных значений признака – 625, а его
дисперсия – 400. Определите величину средней. Х2ср = Х2ср– Хср2
Хср = √( Х2ср- Х2ср) 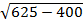 =
=  =15
=15
8.24. Определите ср.величину, если известно,что коэффициент вариации
составляет 30%, а дисперсия признака – 800.
Хср = σ/Vσ * 100% = √σ2 / Vσ *100% = 28,28/30 *100% = 94,28
8.25. Ср.квадратичное отклонение = 25, а ср.величина в совокупности – 15.
Определите ср.квадрат индивидуальных значений этого признака.
σ2= Х2ср – Хср2
Х2ср = 25²+15²=625+225 = 850
8.28. В результате обследования работы банков получено следующее
распределение по доходности активов.
| Группа банков | Доходность,% | Число банков |
| С низким ур-нем информац.технологий | 10-15 | |
| 15-20 | ||
| 20-25 | ||
| С высоким ур-м инф.техн. | 25-30 | |
| 30-35 | ||
| 35-40 | 5 Σ=100 |
Рассчитайте дисперсии:
А) внутригрупповые;
Б) среднюю из внутригрупповых;
В) межгрупповую;
Г) общую, используя правило сложения дисперсий.
Определите эмпирическое корреляционное отношение. Сделайте выводы.
1) Хобщ ср= (12,5*10+17,5*15 +22,5*20+27,5*40+32,5*10+32,5*10+37,5*5)
/ 100 = 2450/100=24,5
σ2= Х2ср – Хср2= 641,25 – 24,52=41,0
σ=√41=6,403%
Vσ= σ/Xcp *100% = 6,403/24,5 *100%=26,1%
2) Xcp = 27,5*40+32,5*10+37.5*5 / 40+10+5 = 1612,5/55 = 29,32
σ2= Х2ср – Хср2
σ2= 869,87 – (29,32)2= 869,87-859,66 = 10,21
σ=√σ2= √10,21 = 3,195%
Vσ= σ/Xcp *100%= 3,195/29,32 *100% = 10,9%
3) межгрупповая дисперсия
σх2= ∑(Хy ср общ – Х0 ср)2ny / ∑ny = (18,64-24,5)2*45 + (29,32 – 24,5)2*55 =
2838,396 / 100 = 28,384%
4) σcp2= ∑σ2j*nj / ∑ny = (15,436)2*45 + (10,21)2*55 / 100 = 164,556
Общ дисперсия
σ02= σcp2 + δ2 = 164б556 + 28б384 = 192б94:
5) Оценка уровня и степени влияния группового признака на вариацию
σ02= ∑(Xj – X0cp)2 / n0 = (12,5 – 24,5)2 + (17,5 – 24,5)2 + (22,5-24,5)2 +
(27,5 – 24,5)2 + (32,5 – 24,5)2 + (37,5 – 24,5)2 / 100 = 41%
9.36.Финансовые органы по способу механического бесповторного отбора
предполагают обследовать на предмет правильности уплаты подоходного
налога 100 малых предприятий. Предельная ошибка выборки не должна
превышать 0,5% при среднем квадратичном отклонении в 2%.
Решение: бесповторный мех.отбор
n=100
δ=0,02
∆=0,5%
N=1050
p=0,997
∆=t*μ t=3
μ =√δ²/n *(1-n/N)
μ =∆/t=0,0005/3=0,000167
0,000167=√0,0004/X*(1-x/1050)=0,000000027=(0,0004/x)*(1050-x/1050)
0,000000027=0,42-0,0004x\1050x
0,000000027=0,0004/x- 0,00000038
0,0004/x=0,000000407
x=982,801
0,00167≠√0,0004/100*(1-100/1050)=0,001902.
9.20.
По результатам 5%-ного выборочного обследования жилищных уел вий 200 семей
города обеспеченность населения жилой площадью х: рактеризуется следующими
данными (способ отбора - случайн-бесповторный ). .
| Размер жилой площади на одного члена семьи, кв.м | Число семей |
| До 5,0 | |
| 5-7 | |
| 7-9 | |
| 9-11 | |
| 11-13 | |
| 13-15 | |
| 15-17 | |
| 17-19 | |
| Более 19 |
Определите:
а) средний размер жилой площади на одного члена семьи;
б) ср квадрат отклон ср размера жилой площади;
В) среднюю ошибку выборки при установлении ср размер жилой площади;
г)предельную ошибку выборки при значении вероятности 0,954;
д)с той же вероятностью - пределы, в которых находится доля се мей,
имеющих размер жилой площади не более 9 м2на человека .
Решение: а)Xср.=4*5+20*6+8*44+10*50+12*16+14*27+16*13+
+18*10+20*9/200=10,83
б)σ²=∑(Xi-Xср.)/∑fi=15,69
в)средняя ошибка выборки
μ=√σ²/n*(1-n/N)=...=√0,07845*(1-0,05)=0,273
n/N=0,05(т.к. 5% воборка)
г)вероятность - 0,945 → t=2 →∆=tµ=2*0,283=0,546
д) 1: 160+120+180+125+140=725
2: 3301
3: 2128
4: 2520
5: 1990
6: 0
9.21. Методом случайной бесповторной выборки обследовали производи тельность
труда 120 рабочих, что составляет 5% численности персонв ла предприятия.
Получены следующие данные:
| Дневн выработка 1 рабочего,Тыс .руб. | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 |
| Кол-во рабочих |
Определите:
а) среднюю дневную выработку одного рабочего;
б) среднюю ошибку выборки при определении производительности труда;
в) предельную ошибку выборки при вероятности 0,954.
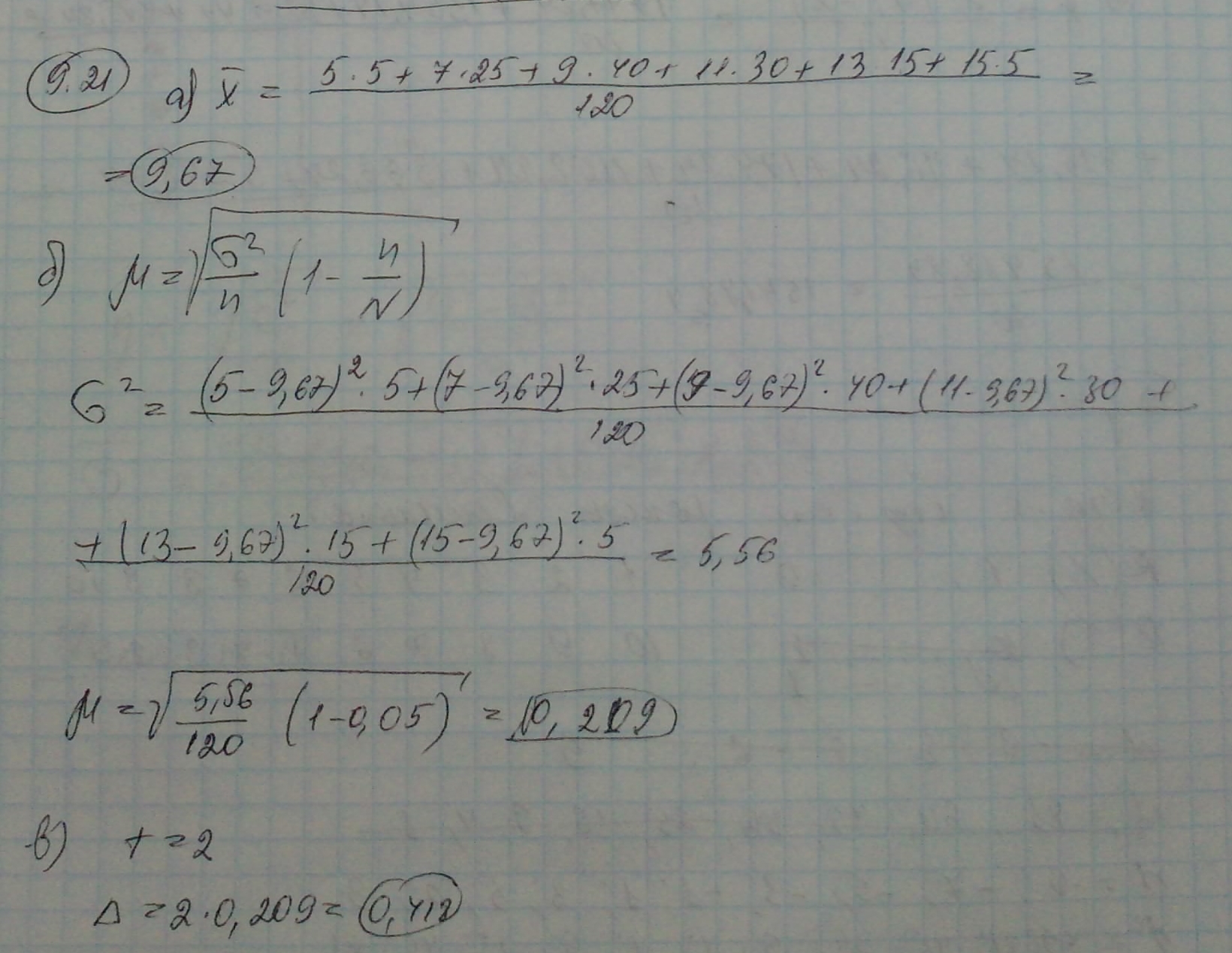
№9.21
Решение:
9.43.Численность одной из двух случайных повторных выборок втрое, а
дисперсия в 1,4 раза меньше, чем другой. Определите, в каком состоянии н
аходятся средние ошибки выборки. Решение:
n1/n2=3
δ2 ²/δ1²=1,4 n1-x
n2=x/3
δ1²=y
δ2 ²=1,4y
μ=√δ²/n
μ1=√x/y=√x/3:1,4y
μ1=√x/3*1,4y=√3*1.4
В √3*1,4 раза ср.ошибка 2 больше 1.
Дата добавления: 2014-12-23; просмотров: 947; Мы поможем в написании вашей работы!; Нарушение авторских прав |