Определение формальной системы

Формальной системой называют множество абстракт­ных объектов, в котором определены правила манипулирова­ния множеством символов, обработанных синтаксическим об­разом, т.е. без учета смысла (семантики). Формальную систему составляют [3]:

1) конечный алфавит (конечное множество симво­лов);

2) процедура образования формул (или слов) фор­мальной системы;

3) множество формул, называемых аксиомами;

4) конечное множество правил вывода, позволяю­щих получать конечное множество формул.

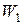Эти правила могут быть представлены в виде и и... и и и... и . Здесь и – формулы формальной системы, а стрелка читается как "влечет" или "следует".

Формальную систему иногда называют аксиоматиче­ской, формальной теорией или просто множеством формул. Алфавит предполагается конечным и его иногда назы­вают словарем. Он содержит константы, переменные и опера­торы.

Процедура образования формул определяет синтаксиче­ское и грамматическое построение символов из уже сформу­лированных символов. Она отличается от правил вывода.

Формальное доказательство (или просто доказательст­во) определяется как конечное множество формул , таких, что каждая формула 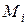либо является аксиомой, либо выводится с помощью правил вывода из предшествующих формул.

Формула t называется теоремой, если существует дока­зательство, в котором она является последней, т.е. . В частности, всякая аксиома является теоремой. Тот факт, что формула является теоремой, обозначается как t. Правила вывода позво­ляют определить, является ли данная формула теоремой дан­ной формальной системы. Различают два типа правил вывода. Правила первого типа применяются к формулам, рассчиты­ваемым как единое целое (в этом случае их называют продук­циями, правилами продукции, или продукционными правила­ми). Правила второго типа могут применяться к любой отдель­ной части формулы, причем сами эти части являются форму­лами. Такие правила назы­вают правилами переписывания.

Так, в математике правило вывода « 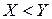и влечет 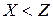» применяется к формуле как к целому. Это продукция с двумя посылками. Слово "влечет" часто заменяется стрелкой . В отличие от предыдущего правила, истинно при любом подвыражении х. Оно является правилом переписывания, и в этом случае для обозначения слова "влечет" используется спе­циальная стрелка .

Пример

1) Алфавит: T, S, A.

2) Формула: любая последовательность символов алфавита.

3) Аксиома: TA.

4) Правила вывода:

a) 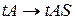(продукция),

b) (продукция),

c) (переписывание),

d) (переписывание).

Правило a является продукцией и применяется только тогда, когда последняя буква теоремы есть A. Таким образом, из теоремы “TASTA” можно вывести “TASTAS”. Следует отметить, что символ t не принадлежит формальной системе и играет роль некоторого слова. Так, правило b позволяет из теоремы “TSA” вывести теорему “TSASA” . Правило c позволяет переход, например, от “TSAAAST” к “TSSST”. Правило d заменяет в “TASSSSV” каждые два S пробелом и в результате получаем “TAV”.

Формальные системы предназначены для получения умозаключений без рассмотрения смысла обрабатываемых заключений. То есть элементы, на основании которых делаете умозаключение, могут быть произвольным образом заменены другими по смыслу элементами.

Например, в абстрактной модели:

“Любой X есть Y.

Если Z есть X,

то Z есть Y.”

используются переменные X, Y, Z. Слова-связи: “если”, “то”, “или” и др. называются операторами.