Семантика языка предикатов первого порядка

Интерпретация формул. Формула имеет определен­ный смысл, т.е. обозначает некоторое высказывание, если су­ществует какая-либо интерпретация. Интерпретировать фор­мулу – это значит связать с ней определенное непустое множе­ство D, т.е. конкретизировать предметную область, называе­мую также областью интерпретации [3] и указать:

· для каждой константы в формуле – конкретный элемент из D;

· для каждой n-местной функциональной буквы в формуле – конкретную n-местную функцию на D;

· для каждой n-местной предикатной буквы в формуле – конкретное отношение между п эле­ментами из D.

Пример

Рассмотрим атом: 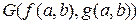и следующую ин­терпретацию:

– множество действительных чисел;

– функция сложения

– функция умножения

– отношение “не меньше”.

При такой интерпретации приведенная ниже формула обозначает высказывание “сумма 2+3 не меньше произведения 2*3”. Это утверждение неверно и поэтому . Если видоизменить интерпретацию, приняв b=1 или b=2, то .

Свойства правильно построенных формул. При за­данной интерпретации значения истинности ППФ можно вычислить по правилам, объединенным в таблице истинности.

Если F и G – любые две ППФ, то значения истинности составного выражения, построенного из этих ППФ, даются таблицей истинности [3] (табл. 3.1).

Т а б л и ц а 2.1

Таблица истинности

F	G
И	И	Л	И	И	И	И
Л	И	И	И	Л	И	Л
И	Л	Л	И	Л	Л	Л
Л	Л	И	Л	Л	И	И

Принцип резолюций. Аппарат логики предикатов используется для представления задачи в виде теоремы: формула Н логически следует из формулы G, т.е. G Н. Доказательство этой теоремы состоит в том, чтобы показать, что каждая интерпретация, удовлетворяющая G, удовлетворяет и Н. С целью упрощения доказательства теоремы все формулы представляются в виде дизъюнкции литералов.

Литералом называется атом или его отрицание. Формулу, представляющую собой дизъюнкцию литералов, называют предложением (или дизъюнктом). Любую ППФ исчисления предикатов первого порядка можно преобразовать во множество предложений [3, 7].

К достоинствам логических моделей относятся единственность теоретического обоснования и возможность реализации системы формально точных определений и выводов. Но попытки представления неформализованных знаний эксперта в системе строгой логики не всегда удается осуществить. Это объясняется нечеткой структурой человеческой логики [2, 3].