
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Синтаксис языка предикатов первого порядка
Предикатом, или логической функцией, называется функция от любого числа аргументов, принимающая истинностные значения: И (истина – 1) и Л (ложь – 0). Аргументы принимают значения из произвольного, конечного или бесконечного множества D, называемого предметной областью. Предикат от п аргументов называют п-местным предикатом [3].
Предикат F(x), определенный на предметной области D, задает определенное свойство элементам множества D и интерпретируется как высказывание “х обладает свойством F”, причем F принимает значение И, если это высказывание истинно, и значение Л, если оно ложно. Предикат  задает отношение между элементами
задает отношение между элементами 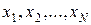 и интерпретируется как высказывание “
и интерпретируется как высказывание “ 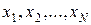 находятся между собой в отношении F”. Пусть, например, D – множество натуральных чисел. Тогда предикат F(x) может обозначать, что “х – четное число" или “х – нечетное число”, а предикат G(x,y) – “х больше у” или “х делится на y” и т.д.
находятся между собой в отношении F”. Пусть, например, D – множество натуральных чисел. Тогда предикат F(x) может обозначать, что “х – четное число" или “х – нечетное число”, а предикат G(x,y) – “х больше у” или “х делится на y” и т.д.
Алфавит языка предикатов первого порядка включает множество следующих символов:
• разделители: запятая, открывающая и закрывающая скобки;
• константы, обозначаемые строчными буквами или соединением таких букв, например “друг”;
• переменные, обозначаемые прописными буквами, например: X, АДРЕС;
• предикаты, обозначаемые прописными буквами, например: Р, Q, БОЛЬШЕ;
• функции, устанавливающие зависимость и отображающие значения одной предметной области в значения другой (или той же), n-местные функции могут служить аргументами предиката. Функции будем обозначать строчными буквами f, g;
• логические операции:
1) “  ” (отрицание или дополнение). Высказывание “
” (отрицание или дополнение). Высказывание “  A” читается “не A”. Оно истинно (И), если высказывание А – ложно (Л);
A” читается “не A”. Оно истинно (И), если высказывание А – ложно (Л);
2) “ 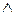 ” (конъюнкция). Высказывание "А
” (конъюнкция). Высказывание "А 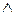 В" читается “А и B”. Оно истинно в том случае, когда истинно как A, так и B;
В" читается “А и B”. Оно истинно в том случае, когда истинно как A, так и B;
3) “  ” (дизъюнкция). Высказывание "А
” (дизъюнкция). Высказывание "А  В" читается “А или B”. Оно истинно, если истинно хотя бы одно из высказываний;
В" читается “А или B”. Оно истинно, если истинно хотя бы одно из высказываний;
4) “  ” (импликация). Высказывание “A
” (импликация). Высказывание “A  B” читается "если A, то B". Оно ложно в том и только в том случае, если A истинно, а B ложно;
B” читается "если A, то B". Оно ложно в том и только в том случае, если A истинно, а B ложно;
5) “  ” (эквивалентность). Высказывание “А
” (эквивалентность). Высказывание “А  В” читается “A тогда и только тогда, когда B”. Оно истинно тогда и только тогда, когда A и B имеют одно и то же истинностное значение;
В” читается “A тогда и только тогда, когда B”. Оно истинно тогда и только тогда, когда A и B имеют одно и то же истинностное значение;
• кванторы:
6) “  ” (квантор существования). Высказывание
” (квантор существования). Высказывание  A читается “существует A”;
A читается “существует A”;
7) “  ” (квантор общности). Высказывание
” (квантор общности). Высказывание  A читается “для любого A”.
A читается “для любого A”.
Пропозициональной формой, илиформулой алгебры логики, называют всякое высказывание, составленное из некоторых исходных высказываний посредством логических операций. Другими словами, если F и G – пропозициональные формы, то  F, (F
F, (F  G), (F
G), (F 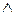 G), (F
G), (F  G) и (F
G) и (F  G) – пропозициональные формы.
G) – пропозициональные формы.
Определение формулы как основного объекта в логике предикатов включает понятие "терм".
Терм – выражение, включающее константы, переменные или n-местные функции  , где
, где  – термы. Например,
– термы. Например, 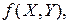 вес(b) – термы.
вес(b) – термы.
Атом,или элементарная (атомная)формула, – это выражение, включающее константы, переменные, функции и предикаты. Таким образом, если Р– N-местный предикат, а  – термы, то
– термы, то  – атом. Например, выражения P(X, зеленый), ABC являются атомами.
– атом. Например, выражения P(X, зеленый), ABC являются атомами.
Формула, или правильно построенная формула, определяется следующим образом:
всякий атом есть ППФ;
если G и Н – ППФ, а Х – переменная, тогда
(  H), (G
H), (G  H), (G
H), (G 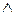 H), (
H), (  X)G, (
X)G, (  X)H – ППФ.
X)H – ППФ.
Примерами ППФ являются:

Выражение "первого порядка" вофразе "исчисление предикатов первого порядка" связано с определением ППФ, в которых запрещается квантифицировать символы предикатов и функций. Например,  не является ППФ логики предикатов первого порядка.
не является ППФ логики предикатов первого порядка.
На практике ППФ используется для представления знаний. Например, ППФ  может выражать "все матери есть женщины", условившись, что M(Х) означает: “X есть мать” и что F(X) означает: “Х – есть женщина”.
может выражать "все матери есть женщины", условившись, что M(Х) означает: “X есть мать” и что F(X) означает: “Х – есть женщина”.
Правилом вывода называют процедуру, которая из одной или нескольких ППФ производит другие ППФ. Например, правило вывода: G и  производит одну ППФ Н; из ППФ
производит одну ППФ Н; из ППФ  и любой константы “а” получают ППФ
и любой константы “а” получают ППФ  , при этом значения X в G заменяются на “а”. Исходные ППФ называют аксиомами, а ППФ, полученные из правил вывода, называют теоремами.
, при этом значения X в G заменяются на “а”. Исходные ППФ называют аксиомами, а ППФ, полученные из правил вывода, называют теоремами.
Дата добавления: 2014-12-23; просмотров: 388; Мы поможем в написании вашей работы!; Нарушение авторских прав |