
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нечеткая логика
Одно из базовых понятий в нечеткой логике это теория нечетких множеств. Эта теория занимается рассмотрением множеств, определяемых небинарными отношениями вхождения. В булевой логике существует только два варианта: либо элемент принадлежит множеству (степень вхождения равна 1), либо не принадлежит ему (степень вхождения равна 0). В нечеткой логике принимается во внимание степень вхождения во множество данного элемента, которая может непрерывно изменяться в интервале от 0 до 1. Указанной степени вхождения элемента во множество соответствует понятие функции принадлежности элемента множеству.
Для комбинирования нецелочисленных значений истинности в нечеткой логике определяются эквиваленты операций  [3, 12]:
[3, 12]:

 (т.е. меньшее);
(т.е. меньшее);

 (т.е. большее);
(т.е. большее);
 (т.е. обратное значение).
(т.е. обратное значение).
Существенной в нечеткой логике является проблема взвешивания сведений. Предположим, что имеется следующий набор продукционных правил:
Правило 1:
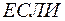
 программирует на ЭВМ
программирует на ЭВМ
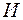
 получает новую информацию через Интернет,
получает новую информацию через Интернет,
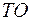
 выберет специальность по информатике.
выберет специальность по информатике.
Правило 2:
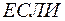
 не склонен к изучению гуманитарных наук
не склонен к изучению гуманитарных наук
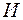
 не любит доказывать теоремы,
не любит доказывать теоремы,
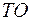
 выберет специальность по информатике.
выберет специальность по информатике.
Предположим, что мы видели, как  программировал задачу на компьютере (определенность равна 1), и вполне уверены (0,8), что
программировал задачу на компьютере (определенность равна 1), и вполне уверены (0,8), что  получает новую информацию через Интернет. Тогда условия, входящие в правило 1, имеют совместное значение степени истинности, равное 0.8, поскольку в случае логической функции
получает новую информацию через Интернет. Тогда условия, входящие в правило 1, имеют совместное значение степени истинности, равное 0.8, поскольку в случае логической функции 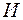 мы используем операцию
мы используем операцию  .
.
Для правила 2 мы знаем, что “  не склонен к изучению гуманитарных наук” (0.5) и “
не склонен к изучению гуманитарных наук” (0.5) и “  не любит доказывать теоремы” (степень истинности 0.25), тогда степень истинности заключения “
не любит доказывать теоремы” (степень истинности 0.25), тогда степень истинности заключения “  выберет специальность по информатике” равна 0.25 (меньшему из значений).
выберет специальность по информатике” равна 0.25 (меньшему из значений).
Таким образом, возникает проблема определения результирующей степени истинности заключения на основании приведенных двух правил. Следует отметить, что исследование таких проблем относится в большей степени к теории свидетельств, чем к нечеткой логике.
Схема, использующая свидетельства, для получения степени уверенности была предложена Шортлиффом и применяется в ЭС MYCIN. Она основывается на коэффициентах уверенности, предназначенных для измерения степени доверия к заключению, которое является результатом полученных свидетельств. Коэффициент уверенности – это разность между двумя мерами:

где 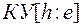 – уверенность в гипотезе
– уверенность в гипотезе  с учетом свидетельства
с учетом свидетельства  ;
;  – мера доверия гипотезе
– мера доверия гипотезе  при заданном свидетельстве
при заданном свидетельстве  ;
; 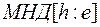 – мера недоверия
– мера недоверия  при свидетельстве
при свидетельстве  .
.
Коэффициент  может изменяться от –1 (абсолютная ложь) до 1 (абсолютная истина). Значения
может изменяться от –1 (абсолютная ложь) до 1 (абсолютная истина). Значения  и
и  могут изменяться только от 0 до 1. Следует отметить, что
могут изменяться только от 0 до 1. Следует отметить, что  ,
,  и
и  не являются вероятностными мерами.
не являются вероятностными мерами.
Шортлиффом была предложена формула уточнения, по которой новую информацию можно сочетать со старыми результатами. Она применяется к мерам доверия и недоверия, связанным с каждой гипотезой. Формула для меры доверия имеет следующий вид:

где запятая между  и
и  означает, что
означает, что  следует за
следует за  . Аналогичным образом уточняются значения меры недоверия.
. Аналогичным образом уточняются значения меры недоверия.
Смысл формулы состоит в том, что влияние второго свидетельства  на гипотезу
на гипотезу  при заданном свидетельстве
при заданном свидетельстве  сказывается в смещении меры доверия в сторону полной определенности на расстояние, зависящее от второго свидетельства. Эта формула имеет два важных свойства:
сказывается в смещении меры доверия в сторону полной определенности на расстояние, зависящее от второго свидетельства. Эта формула имеет два важных свойства:
а) она симметрична относительно следования  и
и  ;
;
б) по мере накопления подкрепляющих свидетельств  (или
(или  ) движется в сторону полной определенности.
) движется в сторону полной определенности.
Рассмотрим пример, указывая в скобках значение  для свидетельств.
для свидетельств.
Правило 1:
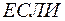
 программирует на ЭВМ (0.75)
программирует на ЭВМ (0.75)
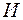
 не любит теоретические дисциплины (0.6),
не любит теоретические дисциплины (0.6),
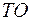
 выберет специальность по информатике.
выберет специальность по информатике.
Правило 2:
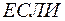
 любит увлекаться точными науками (0.5)
любит увлекаться точными науками (0.5)

 любит практику на ЭВМ (0.7),
любит практику на ЭВМ (0.7),
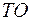
 выберет специальность по информатике.
выберет специальность по информатике.
Операция 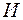 в первом правиле определяет минимальное из значений 0.75 и 0.6 , т.е. 0.6. Операция
в первом правиле определяет минимальное из значений 0.75 и 0.6 , т.е. 0.6. Операция  во втором правиле требует взятия максимального из значений 0.5 и 0.7, т.е. 0.7.
во втором правиле требует взятия максимального из значений 0.5 и 0.7, т.е. 0.7.
Тогда гипотеза, что “  выбирает специальность по информатике” поддерживается на уровне 0.6 правилом 1 и на уровне 0.7 правилом 2. Применяя приведенную формулу, получаем
выбирает специальность по информатике” поддерживается на уровне 0.6 правилом 1 и на уровне 0.7 правилом 2. Применяя приведенную формулу, получаем
МД [информатика: правило 1, правило 2] =
= МД [информатика: правило 1] + МД [информатика: правило 2] 
 (1 − МД [информатика: правило 1]) = 0,88.
(1 − МД [информатика: правило 1]) = 0,88.
Таким образом, объединенная мера доверия оказывается выше, чем при учете каждого свидетельства, взятого отдельно. Это согласуется с ожидаемым нами результатом, поскольку несколько показывающих одно и то же направление свидетельств подкрепляют друг друга. Следует отметить, что если поменять порядок правил 1 и 2, то на результате это не отразится. Такой набор правил с успехом использовался в ЭС MYCIN, что привело к их широкому применению в последующих разработках.
Отношение правдоподобия гипотез. Представляет интерес остановиться на применении теоремы Байеса для связывания информации, поступающей из различных источников [12]. Этот подход позволяет вычислить относительное правдоподобие конкурирующих гипотез исходя из силы свидетельств. В основе применяемого правила лежит формула

где отношение правдоподобия (  ) определяется как вероятность события или свидетельства
) определяется как вероятность события или свидетельства  , при условии заданной конкретной гипотезы
, при условии заданной конкретной гипотезы 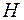 , деленная на вероятность этого свидетельства при условии ложности данной гипотезы (
, деленная на вероятность этого свидетельства при условии ложности данной гипотезы (  ). Таким образом, если мы знаем вероятности свидетельства при заданной гипотезе и ее дополнение, то мы можем определить правдоподобие данной гипотезы на основе имеющегося свидетельства.
). Таким образом, если мы знаем вероятности свидетельства при заданной гипотезе и ее дополнение, то мы можем определить правдоподобие данной гипотезы на основе имеющегося свидетельства.
Например, если мы знаем вероятность появления отличных оценок на вступительном экзамене среди абитуриентов-медалистов и вероятность появления отличных оценок среди остальных абитуриентов, то мы сможем вычислить вероятность того, что абитуриент, сдавший вступительный экзамен на “отлично”, является медалистом.
Отношение правдоподобия может быть использовано для уточнения шансов в пользу рассматриваемой гипотезы, если становится известно, что произошло событие  . Следуя [3, 12], приведем правило Байеса, используя понятие шансов. Шансы
. Следуя [3, 12], приведем правило Байеса, используя понятие шансов. Шансы  за
за 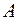 против
против  при наличии некоторого события
при наличии некоторого события 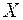 можно записать в виде
можно записать в виде

Полагая  и
и  получаем выражения для соотношений между величинами
получаем выражения для соотношений между величинами  и
и  :
:

Байесовская схема уточнения сводится к выражению [12]

где  – априорные шансы в пользу
– априорные шансы в пользу 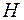 , а
, а  – результирующие апостериорные шансы, при условии наступления события
– результирующие апостериорные шансы, при условии наступления события  , в соответствии с соотношением правдоподобия.
, в соответствии с соотношением правдоподобия.
При этом информация от различных источников может учитываться простым умножением. В случае заданных априорных шансов для конкурирующих гипотез и событий, про которые известно, что они произошли, легко вычисляются апостериорные шансы, а вслед за ними и вероятности. Отношения правдоподобия получаются из двумерной таблицы, показывающей, насколько часто случается каждое событие при каждой из гипотез.
В качестве примера в табл. 4.1 содержатся данные о продолжительности жизни 100 человек. Из них 44 человека прожили более 75 лет, а остальные – 75 лет и меньше, причем указано, кто среди них был курильщиком, а кто – нет.
Таблица 4.1
| Отношение к курению | Продолжительность жизни > 75 лет | Продолжительность жизни 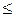 75 лет 75 лет
| Всего |
| Курящие (чел.) | 53 | ||
| Некурящие (чел.) | 47 | ||
| Всего | 44 | 56 | 100 |
Априорные шансы в этой выборке из 100 случаев в пользу того, что человек проживет более 75 лет:

а отношения правдоподобия


Предположим, что пол также принимается во внимание, как еще одна переменная, имеющая отношение к долгожительству (табл. 4.2).
Таблица 4.2
| Пол | Продолжительность жизни > 75 лет | Продолжительность жизни 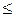 75 лет 75 лет
| Всего |
| Мужчины (чел.) | 56 | ||
| Женщины (чел.) | 44 | ||
| Всего | 44 | 56 | 100 |
Из табл. 4.2 следуют выражения для соотношений правдоподобия для мужчин

и для женщин

Теперь, учитывая, что априорные шансы в пользу продолжительной жизни (свыше 75 лет) равны 11/14 = 0,7857, мы можем вычислить апостериорные шансы того, что курящий мужчина проживет долгую жизнь, пользуясь выражением

Это значение соответствует вероятности 0,3288, тогда как начальная вероятность была 0,44. Таким оказался результат учета двух негативных факторов.
Отношения правдоподобия всегда положительны, причем  указывает на свидетельства в пользу гипотезы,
указывает на свидетельства в пользу гипотезы, 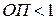 – против нее, а
– против нее, а  говорит о том, что свидетельства не влияют на правдоподобие рассматриваемой гипотезы.
говорит о том, что свидетельства не влияют на правдоподобие рассматриваемой гипотезы.
Множитель 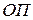 показывает, насколько более вероятной становится данная гипотеза при наличии свидетельств, чем при их отсутствии.
показывает, насколько более вероятной становится данная гипотеза при наличии свидетельств, чем при их отсутствии.
Если свидетельства сами по себе вызывают сомнения, то целесообразно построить масштабированное  , такое, что
, такое, что

где  – вероятность того, что свидетельство надежно. Например, если свидетельство известно с вероятностью
– вероятность того, что свидетельство надежно. Например, если свидетельство известно с вероятностью  , то отношение правдоподобия, равное 1,2 (в пользу гипотезы), согласно приведенному соотношению уменьшится до 1,16.
, то отношение правдоподобия, равное 1,2 (в пользу гипотезы), согласно приведенному соотношению уменьшится до 1,16.
Таким образом, можно сделать вывод, что отношения правдоподобия дают следующие преимущества:
· допускают комбинирование нескольких источников данных;
· возможна их корректировка, если свидетельство ненадежно.
Дата добавления: 2014-12-23; просмотров: 970; Мы поможем в написании вашей работы!; Нарушение авторских прав |