
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нечеткие подмножества
Пусть E есть множество, A – подмножество E, т.е. А  E. Принадлежность любого элемента x подмножеству A можно выразить с помощью функции принадлежности
E. Принадлежность любого элемента x подмножеству A можно выразить с помощью функции принадлежности 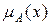 , значения которой указывают, является ли (да или нет) x элементом A:
, значения которой указывают, является ли (да или нет) x элементом A:
 , если
, если  ,
,
 , если
, если  .
.
Предположим теперь, что характеристическая функция для элементов подмножества A может принимать не только значения 0 или 1, но и любое значение а  [0,1], т.е.
[0,1], т.е.  [0,1].
[0,1].
Математический объект, определяемый выражением 
 , где
, где  – элемент универсального множества E, а число после вертикальной черты – значение функции принадлежности для этого элемента, будем называть нечетким подмножеством множества E.
– элемент универсального множества E, а число после вертикальной черты – значение функции принадлежности для этого элемента, будем называть нечетким подмножеством множества E.
На рис. 4.1 приведено графическое представление нечеткого множества с помощью его функции принадлежности [3].

|
| Рис. 4.1. Функция принадлежности |
Строгое определение понятия нечеткого подмножества имеет следующий вид. Пусть E есть множество и x – элемент E. Тогда нечетким подмножеством A множества E называется множество упорядоченных пар
 ,
,
где 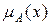 – степень принадлежности x к A. Если
– степень принадлежности x к A. Если 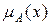 принимает свои значения во множестве M значений функции принадлежности, то можно сказать, что x принимает значения в M посредством
принимает свои значения во множестве M значений функции принадлежности, то можно сказать, что x принимает значения в M посредством  . Множество M называют множеством принадлежностей.
. Множество M называют множеством принадлежностей.
Операции над нечеткими множествами. Рассмотрим различные операции теории обычных множеств применительно к нечетким подмножествам, а также введем новые операции для нечетких подмножеств. Пусть B – множество и М=[0,1] – множество принадлежностей, А и B – два нечетких подмножества из Е.
Равенство. Два нечетких подмножества A и B равны (обозначается A=B) тогда и только тогда, когда
 .
.
Если найдется, по крайней мере, один такой элемент x из E, что равенство  не удовлетворяется, то A и B не равны (
не удовлетворяется, то A и B не равны (  ).
).
Пересечение. Пересечение двух нечетких подмножеств A и B, обозначаемое 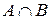 , определяют как наибольшее нечеткое подмножество, содержащееся одновременно в A и B.
, определяют как наибольшее нечеткое подмножество, содержащееся одновременно в A и B.
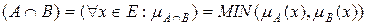 .
.
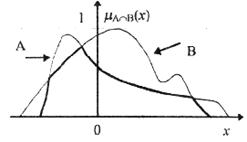
На рис. 4.2 графически представлено пересечение двух нечетких подмножеств.
Объединение. Объединение двух нечетких подмножеств A и B, 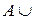 B, определим как наименьшее нечеткое подмножество, которое содержит как A, так и B:
B, определим как наименьшее нечеткое подмножество, которое содержит как A, так и B:
 .
.
На рис. 4.3 графически представлено объединение двух нечетких подмножеств.
| 
|
| Рис. 4.2. Пересечение двух нечетких подмножеств | Рис. 4.3. Объединение двух нечетких подмножеств |
Дополнение.Будем говорить, что A и B – два нечетких подмножества E дополняют друг друга, если
 .
.
Это обозначается следующим образом:
 или
или  .
.
На рис. 4.4 представлено графически дополнение нечеткого подмножества A.
Дизъюнктивная сумма. Дизъюнктивная сумма двух нечетких подмножеств определяется в терминах объединений и пересечений следующим образом [3]:
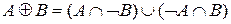 .
.

|
| Рис. 4.4. Дополнение нечеткого подмножества |
Пример







Разность двух подмножеств определяется соотношением
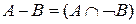 .
.
Используя данные, приведенные в предыдущем примере, получаем

Перемещение. Операция перемещения изменяет значения на величину  . При
. При 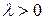 производится перемещение функции вправо, а при
производится перемещение функции вправо, а при  – влево.
– влево.
Соответствующее выражение имеет вид
 .
.
Нормализация.Операция осуществляется в соответствии со следующей формулой:
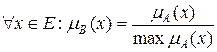 .
.
Дата добавления: 2014-12-23; просмотров: 406; Мы поможем в написании вашей работы!; Нарушение авторских прав |