Пример работы и анализа генетического алгоритма

При использовании генетического алгоритма для решения задачи оптимизации необходимо:

1. Определить количество и тип оптимизируемых переменных задачи, которые необходимо закодировать в хромосоме.

2. Определить критерий оценки особей, задав функцию приспособленности (целевую функцию).

3. Выбрать способ кодирования и его параметры.

4. Определить параметры ГА (размер популяции, тип селекции, генетические операторы и их вероятности, величина разрыва поколений).

Отметим, что параметры ГА, определяемые в пункте 4 (а также, иногда, в пунктах 2 и 3), часто определяются методом проб и ошибок, на основе анализа получаемых результатов. Для анализа результатов работы ГА необходимо произвести несколько запусков алгоритма, для повышения достоверности выводов о качестве получаемых результатов, т.к. результат работы ГА носит вероятностный характер. Описанная общая схема решения задачи с использованием ГА показана на рис. 5.8.

Рассмотрим пример использования ГА для решения задачи минимизации следующей функции (сферическая функция):

(7.1)

Параметр n задает количество переменных функции z. Необходимо найти такие значения переменных x_i , при которых функция z принимает наименьшее значение. Будем использовать общую схему решения (рис. 5.8):

1. Определение неизвестных переменных задачи.По условию поставленной задачи необходимо найти значения переменных x_i, минимизирующие значение функции z, поэтому в хромосоме будем кодировать значения x_i. Таким образом, каждый i-й ген хромосомы будет соответствовать i-й переменной функции z.

2. Задание функции приспособленности. Будем определять приспособленность особи в зависимости от значения, которое принимает функция z при подстановке в нее вектора параметров, соответствующих хромосоме этой особи. Поскольку рассматривается задача минимизации функции z, то будем также считать, что чем меньше значение z, тем приспособленнее особь. Приспособленность i-й особи f_i будем определять по следующей формуле:

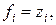
где z_i – значение функции z в точке, соответствующей i-й особи.

Рис. 5.8. Общая схема решения задачи с использованием ГА

3. Выбор способа кодирования. В качестве способа представления генетической информации рассмотрим целочисленное кодирование с точностью кодирования параметров 0,01. Тогда в имеющемся по условию задачи диапазоне изменения значений параметров [–5,12; 5,11] можно закодировать (5,12 – (-5,11))/0,01 + 1 = 1024 различных значений переменной. Единица прибавляется, так как значение переменной равное 0 также учитывается.

Для того чтобы представить 1024 различных значений переменной, достаточно использовать log₂1024 = 10 бит на каждую переменную. Таким образом, будет использоваться целочисленное кодирование с 10-разрядными генами.

4. Определение параметров ГА. Для решения задачи рассмотрим популяцию из 20 особей. При отборе особей для скрещивания будем использовать турнирную селекцию с бинарным турниром. В качестве генетических операторов будем использовать 1-точечный кроссинговер и битовую мутацию. Вероятности применения операторов скрещивания и мутации установим равными 0,7 и 0,05, соответственно. Новое поколение будем формировать только из особей-потомков, т.е. величина разрыва поколений T равна 1.

Результат работы генетического алгоритма с выбранными параметрами представлен на рис. 7.9. Показаны зависимости изменения среднего <z> и наименьшего z_min в популяции значения функции z от номера поколения t. Данные усреднены по 100 независимым запускам.

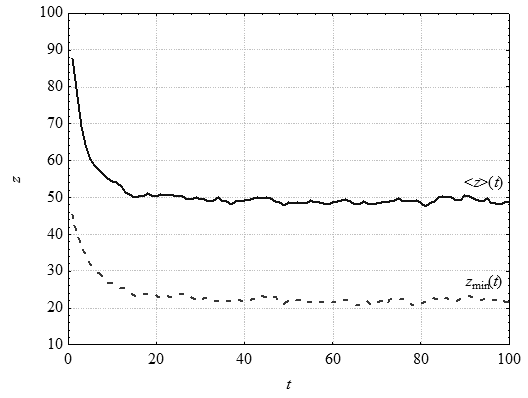
Рис. 5.9. Изменение z_min(t) и <z>(t). Популяция из 20 особей, бинарный турнирный отбор, одноточечный кроссинговер (Р_С = 0,7), битовая мутация (Р_М = 0,05)

По данным рис. 5.9 видно, что после 20-го поколения значение z_min колеблется в достаточно большом диапазоне. Из этого следует, что потери хороших особей в результате мутации велики, и следует уменьшить вероятность мутации. Установим значение этого параметра равным L^-1 = 0,01, где L – длина хромосомы в битах, в данном случае L = 100. Результаты работы ГА с измененным значением вероятности мутации показаны на рис. 5.10.

Рис. 5.10. Изменение z_min(t) и <z>(t). Популяция из 20 особей, бинарный турнирный отбор, одноточечный кроссинговер (Р_С = 0,7), битовая мутация (Р_М = 0,01)

Из сравнения графиков на рис 5.9 и 5.10 следует, что уменьшение вероятности мутации улучшило результат работы ГА. Также отметим, что теперь эволюционный процесс стабилизировался значительно позднее, примерно после 60-го поколения. Усредненное по всем запускам минимальное значение функции z, достигнутое за первые 100 поколений, равно ~1,016. Чтобы улучшить результат, увеличим давление селекции путем увеличения размера турнира до 4. Результат представлен на рис. 5.11.

Увеличение давления селекции привело к ускорению эволюционного поиска за счет удаления из популяции особей со средней и плохой приспособленностью. В результате стабилизация наступила после 40-го поколения, а усредненное по всем запускам минимальное полученное значение функции z равно ~0,013. Наименьшее значение функции z достигается в точке x_i = 0, i = 1,2,…,10 и равно 0. В случае поиска минимума функции z с точностью 0,01, для ГА с параметрами, соответствующими графикам на рис. 5.11, решение было найдено в 69 запусках из 100. При этом в среднем было использовано 1698,68 вычислений целевой функции.

Рис. 5.11. Изменение z_min(t) и <z>(t). Популяция из 20 особей, турнирный отбор (t = 4), одноточечный кроссинговер (Р_С = 0,7), битовая мутация (Р_М = 0,01)

Чтобы повысить стабильность результатов, увеличим размер популяции до 50 особей. Полученные кривые z_min(t) и <z>(t) изображены на рис. 5.12. Во всех 100 запусках найден минимум функции z с точностью не меньше 0,01. Среднее количество вычислений целевой функции, использованное для нахождения решения, равно 3145,34.

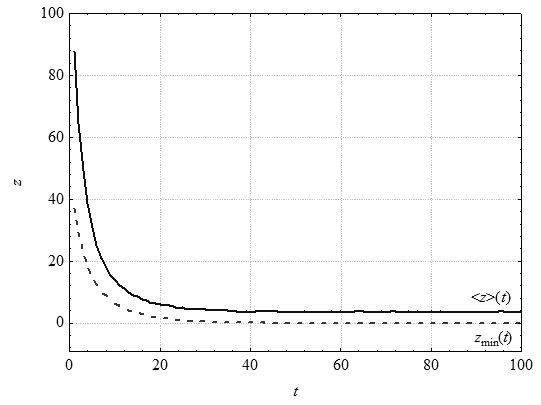
Рис. 5.12. Изменение z_min(t) и <z>(t). Популяция из 50 особей, турнирный отбор (t = 4), одноточечный кроссинговер (Р_С = 0,7), битовая мутация (Р_М = 0,01)