
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Программа работы
1. Изучить схему экспериментальной установки, приведенной на лабораторном стенде.
2. Произвести измерения параметров электрической цепи (фазных и линейных токов и напряжений) в различных режимах работы согласно таблице 9.1.
Таблица 9.1
| № | Вид нагрузки | Iав | Iвс | Iса | Iа | Iв | Iс | Uав | Uвс | Uса |
| А | А | А | А | А | А | В | В | В | ||
| Симметричная нагрузка | ||||||||||
| Обрыв линейного провода | ||||||||||
| Обрыв в фазе потребителя | ||||||||||
| Несимметричная нагрузка |
3. Построить в масштабе по своим данным векторные диаграммы напряжений и токов.
4. По известным фазным токам рассчитать линейные и проверить их соответствие векторным диаграммам и измерениям.
Теоретические положения
Соединение «треугольником» наряду с соединением «звездой» применяется и для генераторов и для приемников электроэнергии. При этом образуется трехфазная трехпроводная система.
В устройствах, для правильной работы которых важно знать направление наводимых ЭДС и создаваемых магнитных полей (генераторы, трансформаторы, электродвигатели), соединение «треугольником» делается следующим образом: конец первой фазы соединяется с началом второй, конец второй с началом третьей, конец третьей с началом первой, а к началам фаз подсоединяется линия электропередачи. Начала фаз маркируются буквами А, В, С, а концы соответственно x, y, z (для генераторов и трансформаторов) (рис. 9.1).

Рис. 9.1
Составив по II закону Кирхгофа уравнение ЭДС для фаз генератора Еф при отключенной линии электропередачи (холостой ход), получим, что  (они равны по модулю и сдвинуты по фазе на 120 градусов). Если в одной из фаз будут перепутаны начало и конец, то в контуре будет действовать двойная фазная ЭДС, а так как сопротивления фаз генератора малы, то будет протекать большой ток. Получим аварийный режим и генератор выйдет из строя на холостом ходу.
(они равны по модулю и сдвинуты по фазе на 120 градусов). Если в одной из фаз будут перепутаны начало и конец, то в контуре будет действовать двойная фазная ЭДС, а так как сопротивления фаз генератора малы, то будет протекать большой ток. Получим аварийный режим и генератор выйдет из строя на холостом ходу.
При соединении приемников энергии «треугольником» его фазные напряжения равны линейным напряжениям цепи. Фазные напряжения, токи и сопротивления обозначаются двумя буквенными индексами (например, Uав, Iав, Zав).
Фазные токи рассчитывают по закону Ома.
Линейные токи определяют по I закону Кирхгофа для соответствующих узлов цепи:
узел «а»:  ;
;
узел «в»:  ; (9.1)
; (9.1)
узел «с»:  .
.
так как трехфазный генератор вырабатывает симметричную систему напряжений (они равны по модулю и сдвинуты по фазе друг от друга на 120 электрических градусов), то при равенстве комплексов сопротивлений фаз потребителя (  ) фазные токи будут также равны по модулю и сдвинуты по фазе относительно соответствующих фазных напряжений на один и тот же угол «φ», а относительно друг друга сдвиг по фазе составит 120 электрических градусов. Имеем симметричный режим работы потребителя – симметричную нагрузку. В этом случае линейные токи, построенные на векторной диаграмме по уравнениям (8.1), будут равны по модулю и в
) фазные токи будут также равны по модулю и сдвинуты по фазе относительно соответствующих фазных напряжений на один и тот же угол «φ», а относительно друг друга сдвиг по фазе составит 120 электрических градусов. Имеем симметричный режим работы потребителя – симметричную нагрузку. В этом случае линейные токи, построенные на векторной диаграмме по уравнениям (8.1), будут равны по модулю и в  раз превышать фазные токи (векторная диаграмма для каждого линейного тока является равнобедренным треугольником с углом при вершине 1200, из которого по теореме косинусов противолежащая сторона в
раз превышать фазные токи (векторная диаграмма для каждого линейного тока является равнобедренным треугольником с углом при вершине 1200, из которого по теореме косинусов противолежащая сторона в  раз больше других сторон).
раз больше других сторон).
При неравенстве комплексов сопротивлений фаз потребителя фазные токи будут отличаться по модулю и фазе, т.е. нагрузка будет несимметричной по фазам.
В этом случае линейные токи можно определить построением векторных диаграмм с соблюдением одного масштаба для токов или рассчитать эти токи по формулам (8.1), используя их изображение в виде комплексных чисел.
В случае активной нагрузки, что имеем в лабораторной работе (ламповый реостат с лампами накаливания можно считать идеальным активным сопротивлением), фазные токи совпадают по фазе с соответствующими напряжениями, а относительно друг друга сдвинуты на 120 градусов. Поэтому линейные токи можно рассчитать по теореме косинусов и при несимметричной нагрузке.
Неполнофазные режимы
Обрыв в фазе потребителя при симметричной нагрузке. В этом случае ток в оборванной фазе равен нулю, (например, Iав = 0). В неповрежденных фазах токи остаются прежними, как и при симметричной нагрузке, так как напряжения на фазах не изменяются. Линейные токи согласно формулам (9.1) будут
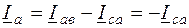 ;
;
 ;
;
 .
.
Схема электрической цепи показана на рисунке 9.2.
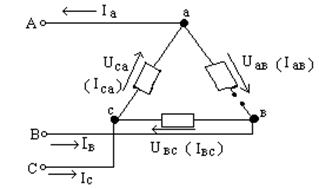
Рис. 9.2
Таким образом, один линейный ток (в нашем примере Iс) не изменится, а два других тока по модулю будут равны фазным токам, а их знак определяет направление линейного тока относительно фазного («+» – токи совпадают по фазе, «–» – линейный ток направлен в противоположном направлении).
Обрыв линейного провода при симметричной нагрузке. При обрыве линейного провода или перегорании одного из предохранителей, которые устанавливаются в линейных проводах, трехфазный потребитель превращается в однофазный с параллельным соединением двух ветвей, в одной из которых два фазных сопротивления будут включены последовательно. Например, Iа = 0, т.е. перегорел предохранитель в этом линейном проводе.
Для этого случая электрическая цепь дана на рисунке 9.3, а основные соотношения будут следующие:
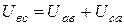 ;
;
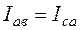 ;
;
 .
.
При симметричной нагрузке
 ;
;
Iв = Ic = 1,5Iвс.

Рис. 9.3
Примерный вид векторных диаграмм для рассмотренных случаев:
1-й опыт 2-й опыт
симметричная нагрузка обрыв линейного провода

3-й опыт 4-й опыт
обрыв в фазе потребителя несимметричная нагрузка

Расчет мощности потребителя
В общем случае для трехфазных приемников потребляемая мощность рассчитывается для каждой фазы в отдельности. Затем суммируются активные и реактивные мощности и определяется полная мощность. Для соединения в «треугольник» имеем:
Р∆ = Рав + Рвс + Рса;
Q∆ = Qав + Qвс + Qса;
 .
.
Фазные мощности находим по формулам:
Рф = IфUф cosφ;
Q = IфUф sinφ.
Только при симметричной нагрузке есть формулы для прямого расчета мощности трехфазного потребителя для соединения в «треугольник» и в «звезду» через линейные параметры:
Р∆/Y =  Uл Iл cosφ;
Uл Iл cosφ;
Q∆/Y =  Uл Iл sinφ;
Uл Iл sinφ;
S∆/Y =  Uл Iл.
Uл Iл.
Контрольные вопросы
1. Как правильно выполнить соединение в «треугольник»?
2. Докажите, что при ошибке в соединении обмоток генератора треугольником в замкнутом контуре будет действовать двойное фазное напряжение. Оцените последствия этой ошибки.
3. Рассчитайте линейные токи по известным фазным при симметричной и несимметричной нагрузке (на примерах).
4. Как изменяется фазные и линейные токи, потребляемая мощность (в относительных единицах), если в нормальном режиме нагрузка была симметричная, а произошли: а) обрыв линейного провода; б) обрыв в фазе потребителя?
Лабораторная работа № 10
Испытание асинхронных двигателей
Цель работы: изучить устройство, принцип действия, схемы включения, методы обнаружения неисправностей трехфазных асинхронных двигателей.
Дата добавления: 2014-12-23; просмотров: 393; Мы поможем в написании вашей работы!; Нарушение авторских прав |