Колебания и волны. 12. Кинематическое уравнение гармонических колебаний материальной точки

12. Кинематическое уравнение гармонических колебаний материальной точки

x = Asin(wt+j₀),

где x – смещение; А – амплитуда колебаний; w - круговая или циклическая частота; j₀ – начальная фаза.

13. Скорость материальной точки, совершающей гармонические колебания

v = Aw cos(wt + j ₀) = v_msin(ωt + φ₀ + π/2).

14. Ускорение материальной точки, совершающей гармонические колебания

a = Aw²sin(wt + j₀) = а_msin(wt + j₀ + π).

15. Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

А =

б) начальная фаза результирующего колебания

16. Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях (x = A₁cosw t, y = A₂cos(w t + j₀)):

а) y = 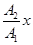(если разность фаз Dj = 0);

б) y = (если разность фаз Dj = ±p);

в) (если разность фаз Dj = ±p/2).

17. Уравнение плоской бегущей волны

y = A cos w (t - ),

где y – смещение любой из точек среды с координатой х в момент t, v – скорость распространения колебаний в среде.

18. Связь разности фаз Dj колебаний с расстоянием Dх между точками среды, отсчитанным в направлении распространения колебаний

,

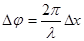где l - длина волны.