ПРОВЕРОЧНЫЙ ТЕСТ 1 страница

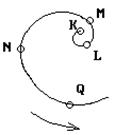
1. Тело движется по траектории, указанной на рисунке, так, что его нормальное ускоре­ние остается постоянным. В какой точке траектории скорость тела наибольшая?

Варианты ответа:

1) Q, 2) N, 3) M, 4) L, 5)K.

2. Мяч падает с высоты h. После отскока его скорость составляет 80% от скорости непосредственно перед ударом об пол. Высота, на которую поднимется мяч после удара, наиболее близка к:

Варианты ответа:

1 ) 0,647h; 2) 0,947h; 3) 0,807h; 4) 0,757h; 5) 0,507h.

3. Камень брошен под углом 60⁰ к горизонту. Как соотносятся между собой начальная кинетическая энергия Т₁ камня с его кинетической энергией Т₂ в верхней точке траектории?

Варианты ответа:

1) Т₁ = 4Т₂; 2) Т₁ = ¾ Т₂; 3) Т₁ = ; 4) Т₁ = Т₂; 5) Т₁ = 2 Т₂.

4. Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси с постоянной угловой скоростью. На внутренней поверхности цилиндра находится небольшое тело, вращающееся вместе с цилиндром. Коэффициент трения между телом и поверхностью цилиндра равен μ. При какой минимальной угловой скорости вращения цилиндра тело еще не будет скользить вниз по поверхности цилиндра?

Варианты ответа: 1) ; 2) ; 3) ; ; .

5. Шарик массой m, подвешенный на нити, качается в вертикальной плоскости так, что его ускорение в крайнем и нижнем положениях равны по модулю друг другу. Если угол отклонения нити в крайнем положении равен α, то сила натяжения нити в нижнем положении равна

Варианты ответа:

1) mg (1+sinα); 2) mg (1+cosα); 3) mg (1-cosα); 4) 3 mg; 5) mg (1-sinα).

6. На вал с насажанным на него колесом диаметром 20 см, относительно оси действует вращающий момент 8 Н×м. С какой минимальной силой должна быть прижата тормозная колодка к ободу вращающегося колеса, чтобы колесо остановилось?

Варианты ответа: 1) 100 Н; 2) 10 Н; 3) 80 Н; 4) 50 Н; 5) 200 Н.

7. Два маленьких шарика А и В из пластилина массой М и 3М соответственно подвешены к потолку на нитях одинаковой дли­ны l. Шарик А отклоняют так, что он поднимается на высоту h и опускают. После столкновения шариков А и В они поднимаются на макси­мальную высоту, равную...

Варианты ответа: 1) (1/16)h; 2) (1/8)h ; 3) (1/4)h; 4) (1/3)h; 5) (1/2)h.

8. Диск начинает вращаться вокруг неподвижной оси; при этом угол поворота j меняется по закону: j = (2t² - t). Чему равны угловая скорость и угловое ускорение диска через 2c?

Варианты ответа:

1) 7 [1/c], 4 [1/с²]; 2) 8 [1/c], 3 [1/с²]; 3) 7 [1/c), 3 (1/с²];

2) 4) 8 [1/c], 4 [1/с²]; 5) 4 [1/c], 4 [1/с²].

9. Человек, стоящий на вращающейся скамье Жуковского, повернул вертикально расположенный в руках стержень в горизонтальное положение. В результате этого у системы:

А. Увеличится момент инерции. Б. Увеличится угловая скорость.

В. Момент импульса не изменится. Г. Увеличится кинетическая энергия.

Варианты ответа: 1) только А и В; 2) только Б и Г; 3) только А, Б и Г;

4) только В; 5) только А.

10. Момент инерции однородного тела зависит от:

А. Момента приложенных к телу сил. Б. Массы тела.

В. Формы и размеров тела. Г. Выбора оси вращения.

Д. Углового ускорения.

Варианты ответа:

1) Б, В и Г; 2) Б и В; 3) А и Д; 4) А, Г и Д; 5) от всех этих факторов.

11. Тело может вращаться относительно оси ОО' под действием сил F₁, F₂, F₃ и F₄ (см. рис.). Момент какой силы относительно ОО' отличен от нуля, если ось вращения и вектора сил лежат в плоскости рисунка?

Варианты ответа:

1) моменты всех сил относительно оси ОО' равны нулю

2) F₁; 3) F₂; 4) F₃; 5) F_4.

12. На рисунке приведены 2 маятника, отличающиеся положением грузов на невесомом стержне. Указать верные утверждения для этих маятников.

А. Момент инерции маятника I больше момента инерции маятника II.

Б. Оба маятника имеют одинаковую частоту колебаний.

В. Период колебаний маятника зависит как от его момента инерции, так и от положения центра масс.

Г. Маятник I можно считать математическим.

Д. Период колебаний маятника I больше периода колебаний маятника

Варианты ответа:

1) А, В, Г, Д; 2) В, Г, Д; 3) В, Д; 4) А, Б, В; 5) Б, Г.

13. Крутильный маятник представляет собой вертикальную проволоку, на нижнем конце которой закреплен очень легкий горизонтальный стержень с двумя грузами небольших размеров. Во сколько раз изменится период колебаний маятника, если расстояние от оси вращения до грузов увеличить в два раза?

Варианты ответа:

1) увеличится в 2 раза; 2) увеличится в 4 раза; 3) увеличится в раз;

4) уменьшится раз; 5) уменьшится в 2 раза.

14. Маятник настенных механических часов представляет собой легкий стержень с гpузиком. Для регулировки точности хода часов гpузик можно перемещать по стержню. Как изменится период колебаний маятника, если гpузик переместить с конца стержня на середину?

Варианты ответа:

1) уменьшится раз ; 2) увеличится в 2 раза; 3) увеличится в 4 раза ;

4) увеличится в раз; 5) уменьшится в 2 раза.

15. Частица может колебаться вдоль оси x под действием результирующей силы F = -k x с амплитудой А и частотой w, где k - поло­жительная константа. В момент, когда x = A/2, скорость частицы будет равна:

Варианты ответа:

1) Аw ; 2) 2w А; 3) w А; 4) w А; 5) (1/3) w А.

16. Момент инерции однородного диска массойm и радиусомR от­носительно оси, проходящей через его центр масс перпендикулярно плоскости диска, равен J = ¹/₂ mR ². Чему равен момент инерции диска относительно оси, проходящей через его край и перпендикулярной плоскости диска?

Варианты ответа: 1) ³/₂ mR²; 2) ¹/₂ mR² ; 3) mR² ; 4) 0,4 mR² ; 5) 2mR² .

17. Момент импульса тела относительно неподвижной оси изменяет­ся по закону L = at². Какой из графиков правильно отражает зависимость величины момента сил, действующих на тело?

Варианты ответов:

1) с

2) a

3) b

4) e

5) d.

18. На твердое тело, находившееся в состоянии покоя, начал действовать постоянный момент силы. При этом:

А. момент импульса тела стал увеличиваться;

В. момент инерции тела стал увеличиваться;

С. кинетическая энергия тела стала увеличиваться;

D. угловое ускорение тела стало увеличиваться.

Варианты ответов:

1) только А и В; 2) только С; 3) только С и D; 4) В, С и D; 5) А, В, С и D.

19. Если координаты тела массой m = 10 кг, движущегося прямолинейно вдоль оси х, меняются со временем по закону x = 10t (1-2t) м, то модуль силы, действующий на тело равен

Варианты ответа: 1) 400 Н; 2) 0 Н; 3) 10 Н; 4) 20 Н; 40 Н.

20. Уравнение y = A sin 2p (t/T - x/L), где А,T,l - положительные величины, описывает волну, для которой ...

Варианты ответа:

1) скорость равна l/T; 2) амплитуда равна 2А; 3) скорость направлена вдоль отрицательной оси x; 4) период равен T/p; 5) скорость равна x/t;

4.4. КОНТРОЛЬНАЯ РАБОТА №1

100. Материальная точка движется по окружности с постоянной угловой скоростью рад/с. Во сколько раз путь DS, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения D ? Принять, что в момент начала отсчета времени радиус-вектор , задающий положение точки на окружности, относительно исходного положения был повернут на угол рад.

101. Материальная точка движется прямолинейно с ускорением а = 5 м/с². Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду? Принять v₀ = 0.

102. Точка движется по окружности радиусом R = 20 см c постоянным ускорением а_t = 5 см/с². Через какое время после начала движения нормальное ускорение а_n точки будет: равно тангенциальному; 2) вдвое больше тангенциального?

103. Точка движется по окружности радиусом R = 30cм c постоянным угловым ускорением e. Определить тангенциальное ускорение а_t точки, если известно, что за время t = 4 c она совершила три оборота и в конце третьего оборота ее нормальное ускорение а_n = 2,7 м/с². Рассмотреть два случая: e >0, e<0.

104. Линейная скорость точек на окружности вращающегося диска v₁ =3 м/с. Точки, расположенные на 10 см ближе к оси, имеют линейную скорость v₂ =2 м/с. Сколько оборотов в секунду делает диск?

105. Первую половину пути тело двигалось со скоростью v₁ =2 м/с, вторую половину пути со скоростью V₂ =8 м/с. Определить среднюю скорость движения.

106. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а_t. Найти нормальное ускорение а_n точки через t = 20 с после начала движения. Если известно, что к концу пятого оборота после начала движения линейная скорость точки равна v = 10 см/с.

107. Точка движется по прямой согласно уравнению: x = At + Bt³, где А = 6 м/с, В = -0,125 м/с³. Определить среднюю путевую скорость <v> точки в интервале времени от t₁ = 2 c до t₂ = 6 c.

108. Движение точки по прямой задано уравнением x =At +Bt², где А = 2 м/с, В = (-0,5)м/с². Определить среднюю скорость движения точки в интервале времени от t₁ =1c до t₂ =3c.

109. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью v₁ = 1 м/с и ускорением a₁=2 м/с², вторая – с начальной скоростью v₂=10 м/с и ускорением а₂=1 м/с². Когда и где вторая точка догонит первую?

110. Мяч бросили со скоростью 10 м/с под углом 40⁰ к горизонту. Найти: на какую высоту поднимется мяч, на каком расстоянии от места бросания мяч упадет на землю, какое время он будет в движении?

111. Камень брошен в горизонтальном направлении. Через 0,5 с после начала движения численное значение скорости камня стало в 1,5 раза больше его начальной скорости. Найти начальную скорость камня. Сопротивление воздуха не учитывать.

112. С вышки бросили камень в горизонтальном направлении. Через 2 с камень упал на землю на расстоянии S = 40 м от основания вышки, Определить начальную v_о и конечную v скорости камня.

113. Пуля выпущена с начальной скоростью v_о =200 м/с под углом a =60 ^о к плоскости горизонта. Определить наибольшую высоту H подъема, дальность S ее полета. Сопротивлением воздуха пренебречь.

114. Тело брошено под углом a = 30⁰ к горизонту со скоростью v₀ = 30 м/с. Каковы будут нормальное a_n и тангенциальное а_t ускорения тела через время t = 1 с после начала движения?

115. Тело брошено под углом φ =30⁰ к горизонту. Найти тангенциальное а_τ и нормальное а_n ускорения в начальный момент движения.

116. Тело брошено со скоростью v₀ под углом к горизонту. Продолжительность полета 2,2 с. Найти наибольшую высоту поднятия этого тела.

117. Камень брошен горизонтально со скоростью v₀ = 15 м/с. Найти нормальное и тангенциальное ускорение камня через 1 с после начала движения.

118. Камень брошен вертикально вверх с начальной скоростью v_о = 20 м/с. Через сколько секунд камень будет находиться на высоте h =15 м? Какова будет скорость камня на этой высоте? Сопротивлением воздуха пренебречь.

119. С башни высотой H =25 м горизонтально брошен камень со скоростью v_о =15 м/с. Какое время камень будет в движении? На каком расстоянии S от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория камня с горизонтом в точке его падения на землю? Сопротивлением воздуха пренебречь.

120. К пружинным весам подвешен блок. Через блок перекинули шнур, к концам которого привязали грузы массой m₁ = 1,5 кг и m₂ = 3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь.

121. На барабан радиусом R =0,5 м намотан шнур, к концу которого привязан груз массой m =10 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением а =2,04 м/с² ?

122. На концах нити, переброшенной через блок, висят на одинаковой высоте две гирьки массой по 96 г каждая. Если на одну из них положить перегрузок, вся система придет в движение и через 3 с расстояние между гирьками станет равным 1,8 м. Определить: вес перегрузка, силу натяжения нити, силу давления перегрузка на гирьку и силу давления на ось блока.

123. К концам нити, перекинутой через блок, укрепленный на динамометре, подвешены два груза массой 0,1 и 0,2 кг. Определить ускорение грузов, натяжение нити и показание динамометра.

124. Грузик, привязанный к нити длиной l = 1 м, описывает окружность в горизонтальной плоскости. Определить период Т обращения, если нить отклонена на угол j = 60⁰ от вертикали.

125. К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой – вдоль вертикали вниз. Определить коэффициент трения между поверхностями груза и стола, если масса каждого груза и блока одинаковы и грузы движутся с ускорением а = 2,6 м/с². Трением в блоке пренебречь.

126. Блок, имеющий форму диска массой m = 0,4 кг вращается под действием силы натяжения нити, к концам которой подвешены грузы m₁ = 0,3 кг и m₂ = 0,7 кг. Определить силы натяжения Т₁ и Т₂ нити по обе стороны блока.

127. Нить с привязанными к ее концам грузами m₁ = 50 г и m₂ = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции блока I , если под действием силы тяжести грузов он получил угловое ускорение e = 1,5 рад/с². Трением и проскальзыванием нити по блоку пренебречь.

128. Тонкий стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением e = 3 рад/с² около оси, проходящей через середину стержня перпендикулярно к его длине. Определить вращающий момент М.

129. По ободу шкива, насажанного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой m = 1 кг. На какое расстояние h должен опуститься груз, чтобы колесо со шкивом получило частоту вращения n = 60 об/мин? Момент инерции колеса со шкивом I = 0, 42 кг×м², радиус шкива R = 10 см.

130. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом a = 30⁰ к линии горизонта. Определить скорость u₂ отката платформы, если снаряд вылетает со скоростью u₁ = 480 м/с. Масса платформы с орудием и снарядами m₂ = 18 т, масса снаряда m₁ = 60 кг.

131. Снаряд массой m = 10 кг, обладал скоростью v = 200 м/с в верхней точке траектории. В этой точке он разорвался на две части. Меньшая часть массой m₁ = 3 кг, получила скорость u₁ = 400 м/с в прежнем направлении. Найти скорость u₂ второй, большей части, после разрыва.

132. С тележки, свободно движущейся по горизонтальному пути со скоростью v₁ = 3 м/с, в сторону, противоположную движению тележки, спрыгнул человек, после чего скорость тележки изменилась и стала равной u₁ = 4 м/с. Определить горизонтальную составляющую скорости u₂ человека при прыжке относительно тележки. Масса тележки m₁ = 210 кг, масса человека m₂ = 70 кг.

133. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце стоит человек. Масса его m₁ = 60 кг, масса доски m₂ = 20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) v = 1 м/с? Массой колес и трением пренебречь.

134. Человек массой m₁= 70 кг, бегущий со скоростью v₁ = 9 км/час, догоняет тележку массой m₂ = 190 кг, движущуюся со скоростью v₂ = 3,6 км/час, и вскакивает на нее. С какой скоростью будет двигаться тележка с человеком?

135. На сколько переместится относительно берега лодка длиной l = 3,5 м и массой m₁ = 200 кг, если стоящий на корме человек массой m₂ = 80 кг переместился на нос лодки? Считать лодку расположенной перпендикулярно берегу.

136. Определить импульс, полученный стенкой при ударе о нее шарика массой m = 300 г, если шарик двигался со скоростью v = 8 м/с под углом a = 60⁰ к плоскости стенки. Удар считать упругим.

137. С высоты h₁ = 2 м на стальную плиту свободно падает шарик массой m = 200 г и подпрыгивает на высоту h₂ = 0,5 м. Определить импульс, полученный плитой при ударе.

138. Человек и тележка движутся навстречу друг другу, причем масса человека в два раза больше массы тележки. Скорость человека 2 м/с, а тележки – 1 м/с. Человек вскакивает на тележку и остается на ней. Какова скорость человека с тележкой?

139. Снаряд массой m =10 кг обладал скоростью v = 200 м/с в верхней точке траектории. В этой точке он разорвался на две части. Меньшая часть массой m₁ =3 кг получила скорость v₁ = 400 м/с в прежнем направлении под углом φ =60^о к горизонту. С какой скоростью и в каком направлении полетит большая часть снаряда?

140. Тело массой m₁ =2 кг движется навстречу второму телу, масса которого m₂ =1,5 кг, и не упруго сталкивается с ним. Скорость тел непосредственно перед столкновением была равна соответственно v₁ = 1 м/с и v₂ =2 м/с. Какое время будут двигаться эти тела после столкновения, если коэффициент трения k=0,05 ?

141. На горизонтальном столе лежит брусок массой 5 кг. В брусок попадает пуля массой 10 г, летящая горизонтально со скоростью 500 м/с. Какое расстояние пройдет брусок по столу до полной остановки? Коэффициент трения бруска о стол k=0,05.

142. Вычислить работу, совершаемую при равноускоренном подъеме груза массой 100 кг на высоту 4 м за время 2 с.

143. Под действием груза в 20 Н, подвешенного к пружине, пружина растянулась на 10 см. Определить потенциальную энергию пружины.

144. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сжимается на Dl = 3 мм. На сколько сожмет пружину тот же груз, упавший на ее конец с высоты h = 8 см?

145. Конькобежец, стоя на льду, бросил вперед гирю массой m₁= 5 кг и вследствие отдачи покатился назад со скоростью u₂ = 1 м/с. Масса конькобежца m₂ = 60 кг. Определить работу, совершенную конькобежцем при бросании гири.

146. Сплошной однородный диск катится по горизонтальной плоскости со скоростью 10 м/с. Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент сопротивления движению диска равен 0,02.

147. Сплошной цилиндр скатился с наклонной плоскости высотой 15 см. Какую скорость поступательного движения будет иметь цилиндр в конце наклонной плоскости?

148. В деревянный шар массой m₁ = 8 кг, подвешенный на нити длиной 1,8 м, попадает горизонтально летящая пуля массой m₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол a = 3⁰? Размером шара пренебречь. Удар прямой, центральный.

149. Атом распадается на две части массами m₁ = 1,6 10^-25 кг и m₂ =2,3 10^-25 кг. Определить кинетические энергии Т₁ и Т₂ частей атома, если их общая кинетическая энергия Т = 2,2 10^-11 Дж. Кинетической энергией и импульсом атома до распада пренебречь.

150. Горизонтальная платформа массой 200 кг вращается вокруг горизонтальной оси, проходящей через центр платформы, делая 10 об/с. Человек массой 60 кг стоит на расстоянии R от центра платформы. Сколько оборотов в секунду будет делать платформа, если расстояние человека от центра платформы станет равным R/2? Платформа - однородный диск радиусом R м, человек - точечная масса.

151. На краю горизонтальной неподвижной платформы, имеющей форму диска радиусом 2 м, стоит человек. Масса платформы 200 кг, масса человека 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью 2 м/с относительно платформы.

152. В центре скамьи Жуковского стоит человек и держит в руках металлический стержень длиной l = 1,5 м и массой 8 кг вертикально по оси вращения. При этом скамейка с человеком вращается с частотой n₁ = 4 об/с. Момент инерции человека и скамейки I = 6 кг м². Сколько оборотов в секунду будет делать скамья с человеком, если человек повернет стержень в горизонтальное положение, причем центр масс стержня находится на расстоянии l/3 от оси.

153. Платформа в виде диска радиусом 1 м вращается по инерции с частотой 6 об/мин. На краю платформы стоит человек, масса которого 80 кг. С какой частотой будет вращаться платформа, если человек перейдет в её центр? Момент инерции платформы 120 кг∙м². Момент инерции человека рассчитывать как для материальной точки.

154. Деревянный стержень массой m = 1 кг и длиной l = 0,4 м может вращаться около оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 0,01 кг, летящая перпендикулярно стержню со скоростью 200 м/с. Сколько оборотов в секунду будет делать стержень, если пуля застрянет в нем?

155. На скамье Жуковского, вращающейся около вертикальной оси с частотой 2 об/с, стоит человек и держит на вытянутых руках две одинаковые гири. Расстояние между гирями равно 1,5 м. Когда человек опускает руки, расстояние между гирями становится равным 0,4 м и частота вращения скамьи 3 об/с. Момент инерции человека и скамьи 8 кг м². Трением пренебречь. Определить массу гири.

156. Платформа в виде диска диаметром D = 3 м и массой m₁ = 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью w₁ будет вращаться эта платформа, если по ее краю пойдет человек массой m₂ = 70 кг со скоростью v = 1,8 м/с относительно платформы?

157. Горизонтальная платформа массой m =100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n₁ =10 об/мин. Человек массой m =60 кг стоит при этом на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек перейдет от края платформы к её центру. Считать платформу однородным диском, а человека – точечной массой.

158. Однородный стержень длиной l = 1 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно не упруго ударяет пуля массой m = 7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонился на угол a = 60⁰. Принять скорость пули v = 360 м/с. Масса стержня много больше массы пули.

159. В центре скамьи Жуковского стоит человек и держит в руках металлический стержень длиной l = 1,5 м и массой 8 кг вертикально оси вращения. При этом скамейка с человеком вращается с частотой n = 4 об/с. Момент инерции человека скамейки I = 6 кг×м²_. Сколько оборотов в секунду будет делать скамья с человеком, если человек повернет стержень в горизонтальное положение, причем человек держит стержень за конец?

160. На каком расстоянии от поверхности Земли ускорение свободного падения равно 1 м/c²?

161. Сравнить ускорение силы тяжести на поверхности Луны с ускорением силы тяжести на поверхности Земли.

162. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84×10⁸м?