Лекція 17. Системи диференціальних рівнянь.

Задача Коші полягає в розв’язку системи звичайних диференційних рівнянь першого порядку, яка має вигляд:

(1)

Розв’язок одного диференційного рівняння методом Рунге-Кута виконується по вказаним формулам, якщо в них опустити індекс , а з алгоритму видалити цикли. Це різко спрощаує програму і дозволяє отримати мінімально можливий час розрахунку.

яка має похибку ~ , обчислюються наступними формулами

де j [1, N]-номер кожної змінної -незалежна змінна. Розв’язок системи (1) при заданих початкових умовах зводиться до знаходження залежностей (інтегральних кривих) які проходять через точки, задані початковими умовами Задача Коші зводиться до інтегрування диференційних рівнянь.

Загальна форма запису кожного рівняння системи (1) може бути такою:

dY_j /dx = F_j(x, Y_j) (2)

де 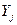в правій частині рівняння - вектори змінних , а - права частина кожного з рівнянь (1). Зокрема, одне диференційне рівняння ( 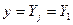и ) запишеться у вигляді: