
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проекційні методи (на прикладі методу Гальоркіна).
Сутність проекційних методів обчислювальної математики полягає в представленні розв’язку задачі множиною проекцій (відліків) у визначеній системі координатних функцій.
У традиційному методі, запропонованому Б. П. Гальоркіним і розвинутому у роботах М. В. Келдиша, наближений розв’язок у(х) відшукується у вигляді
yn = a1u1(x) + a2u2 + ... + anun(x), (7)
де j1(x), j2, ,,, , jn(x), – система базисних функцій, що задовольняють вихідним граничним умовам; a1, a2, ... , an – невідомі постійні коефіцієнти.
При підстановці (7) у (1) одержуємо функцію
R(x; a1; a2; ... ; an) = L[yn(x)] – f(x),
яку називають нев'язкою розв’язку. Очевидно, для точного розв’язку задачі
R(x; a1; a2; ... ; an) = 0.
Коефіцієнти аi визначимо з умови ортогональності нев'язки першим n функціям деякої системи функцій {ji, i = 0 ... n}:
 (8)
(8)
Такий метод розв’язку задачі називається методом моментів.
Якщо при цьому ji=ui, то виходить метод Гальоркіна. Система рівнянь (8) являє собою систему лінійних рівнянь щодо вектора  з матрицею
з матрицею
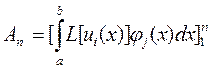 .
.
Розв’язок цієї системи є каркасом наближеного розв’язку крайової задачі.
Система (8) може бути представлена у вигляді
 . (9)
. (9)
Коефіцієнти cki, di, обчислюються по формулах

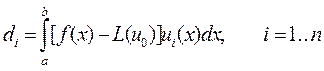
Для рівняння (1) L(y) = y¢¢ - p(x)y¢ - q(x)y.
Тому
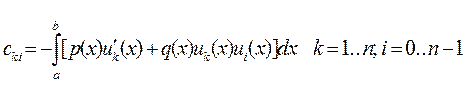
cik = cki

Функцію u0(x) можна вибирати довільно, але так щоб u0(a)=A, u0(b)=B. Нехай u0(x) = a + bx. Тоді з (2) одержуємо:

Інші функції ui(x) можна обчислити по кожному з правил:
ui(x) = (x – a)i(x – b);
ui(x) = (x – a)(x – b)i.
ОБЧИСЛЮВАЛЬНІ СХЕМИ
Дата добавления: 2014-12-23; просмотров: 340; Мы поможем в написании вашей работы!; Нарушение авторских прав |