Дифференціальні рівняння вищого порядку

(3)

де порядок рівняння, можна звести до системи типу (1) чи (2) з допомогою таких перетворень:

(4)

Таким чином, розв’язок (3) зводиться до розв’язку системи диференційних рівнянь першого порядку.(4).

Метод Ейлера – простий метод першого порядку. Він реалізується наступною рекурентною формулою:

Y_j(i+1) = Y_ji + hF_j(x_i, Y_ji)

де - шаг інтегрування. Метод має похибку пропорційну .

Метод Ейлера- Коші с ітераціями полягає в розрахунку на кожному кроці проміжного значення:

Розв’язок уточнюється ітераційною формулою

Метод має похибку R пропорційну ~ 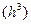. Число ітерацій не повинно бути більше 4, інакше слід зменьшити шаг .

Модифікований метод Ейлера другого порядку реалізується наступними рекурентними формулами:

Y_j(i+1) = Y_ji + hF_j(x_i +h/2,Y_j(i+1/2))

де Y_j(i+1/2) = Y_ji + hF_j(x_i, Y_ji)/2. Метод має похибку R пропорційну ~ (h³), та менший час обчислень.

Метод трапецій - один з модифікацій методу Эйлера другого порядку. Він реалізується формулою:

Y_j(i+1) = Y_ji + (K_j1 + K_j2)/2

де K_j1 = hF_j(x_i, Y_ji), K_j2 = hF_j(x_i,+h, Y_ji + K_j1), дає похибку R ~ .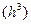

Не рекомендується використовувати цей метод, коли пошукова функція має різну крутизну.

Метод Рунге-Кута четвертого порядку є найбільш розповсюдженим при постійному . У нього висока точність - похибка R ~ - і менший нахил до розбіжності розв’язку. Алгоритм реалізації методу Рунге-Кута полягає в циклічних обчисленнях на кожному кроці по таким формулам:

K_1j = hF_j(x_i, Y_ji)

K_2j = hF_j(x_i,+h/2, Y_ji + K_1j /2)

K_3j = hF_j(x_i,+h/2, Y_ji + K_2j /2)

K_4j = hF_j(x_i,+h, Y_ji + K_3j )

Y_j(i+1) = Y_ji + (K_1j + 2K_2j + 2K_3j + K_4j)/6

При переході від однієї формули до іншої задаються або обчислюються відповідні значення x_i и y_i та підпрограмою значення функції .

Перед початком циклу потрібно задати шаг і початкові значення:

Метод Рунге-Кута для диференційного рівняння другого порядку виду

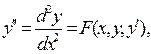
Спочатку потрібно задати шаг і початкові значення: 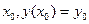та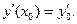

Розв’язок одного диференційного рівняння методом Рунге-Кута виконується по вказаним формулам, якщо в них опустити індекс , а з алгоритму видалити цикли. Це різко спрощаує програму і дозволяє отримати мінімально можливий час розрахунку.

яка має похибку ~ , обчислюються наступними формулами:

Лекція 18. МЕТОДИ РОЗВ’ЯЗКУ КРАЙОВИХ ЗАДАЧ

Методи розв’язку крайових задач розглядаються на прикладі звичайного диференціального рівняння другого порядку

y¢¢ + p(x)y¢ + q(x)y = f(x) (1)

при граничних умовах

a0y(a) + a₁y¢ (a) = A, (2)

b₀y(b) + b₁y¢ (b) = B;

при |a₀| + |a₁| ¹ 0, |b₀| + |b₁| ¹ 0, a £ x £ b. (де a₀, a₁, b₀, b₁, a, b, A, B – деякі числа).

Методи розв’язку крайових задач можна розділити на три групи: різницеві, проекційні і методи, засновані на заміні розв’язку крайової задачі розв’язком декількох задач Коші (методи «стрільби»).