
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа связывает термодинамические параметры газа с параметрами, характеризующими движение его молекул. Так, давление газа, как следствие соударений молекул газа со стенками сосуда, определяется, согласно основному уравнению молекулярно-кинетической теории идеального газа, кинетической энергией поступательного движения молекул газа.
 При выводе основного уравнения молекулярно-кинетической теории идеального газа полагают, что соударения молекул газа со стенками сосуда являются абсолютно упругими. Тогда, при соударении одна молекула газа массой m0, движущаяся перпендикулярно стенке сосуда со скоростью
При выводе основного уравнения молекулярно-кинетической теории идеального газа полагают, что соударения молекул газа со стенками сосуда являются абсолютно упругими. Тогда, при соударении одна молекула газа массой m0, движущаяся перпендикулярно стенке сосуда со скоростью  , передает ей импульс
, передает ей импульс  .
.
Выделив на стенке сосуда элементарную площадку DS (рис. 1), определяют давление газа p на эту площадку. Построив цилиндр с основанием DS и высотой  (рис. 1), учитывают, что число молекул, способных за время Dt достигнуть площадки DS соответствует Рис. 1
(рис. 1), учитывают, что число молекул, способных за время Dt достигнуть площадки DS соответствует Рис. 1
1/6 части всех N молекул, содержащихся в объеме выделенного цилиндра (  , где n – концентрация молекул). Коэффициент 1/6 учитывает, что из всех N молекул, движущихся хаотично вдоль трех (x, y, z) взаимно перпендикулярных направлений, только их 1/6 часть движется по направлению к площадке DS. Тогда число ударов молекул, движущихся в данном направлении, о площадку DS за время Dt будет равно:
, где n – концентрация молекул). Коэффициент 1/6 учитывает, что из всех N молекул, движущихся хаотично вдоль трех (x, y, z) взаимно перпендикулярных направлений, только их 1/6 часть движется по направлению к площадке DS. Тогда число ударов молекул, движущихся в данном направлении, о площадку DS за время Dt будет равно:  .
.
При столкновении с площадкой DS эти молекулы передадут ей импульс DP :
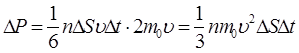 ,
,
что соответствует, согласно второму закону Ньютона, действию силы F :
 .
.
Тогда давление газа, оказываемое им на стенки сосуда:
 .
.
Однако, молекулы газа движутся с различными скоростями  ,
,  ,….
,….  , что можно учесть в полученной формуле, введя понятие средней квадратичной скоростидвижения молекул
, что можно учесть в полученной формуле, введя понятие средней квадратичной скоростидвижения молекул  :
:
 , тогда
, тогда  .
.
Так как  , а
, а  – средняя кинетическая энергия движения одноатомной молекулы, то получим:
– средняя кинетическая энергия движения одноатомной молекулы, то получим:
 ,
,
где Е – суммарная кинетическая энергия всех молекул газа,  .
.
Таким образом, получены два эквивалентных уравнения:
 и
и  ,
,
связывающие кинематические параметры движения отдельных молекул газа с термодинамическими параметрами газа в целом, каждое из которых называют основным уравнением молекулярно-кинетической теории идеального газа.
Из сравнения между собой уравнений  и
и  следует, что
следует, что
 ,
,
то есть еще одно уравнение, связывающее термодинамический параметр газа (Т) со средней кинетической энергией молекулы одноатомного газа  .
.
С другой стороны, величина средней кинетической энергии молекул газа  определяется температурой газа Т (для случая одноатомного газа):
определяется температурой газа Т (для случая одноатомного газа):
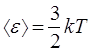 .
.
Дата добавления: 2014-12-23; просмотров: 280; Мы поможем в написании вашей работы!; Нарушение авторских прав |