
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 4. Распределение молекул идеального газа по скоростям.
В газе, находящемся в состоянии равновесия при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Максвелл установил, что это распределение для идеального газа описывается некоторой функцией  , называемой функцией распределения молекул газа по скоростям.
, называемой функцией распределения молекул газа по скоростям.
Если разбить диапазон скоростей молекул на малые интервалы, равные  , то на каждый интервал скорости будет приходиться некоторое число молекул
, то на каждый интервал скорости будет приходиться некоторое число молекул 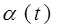 , имеющих скорость, заключенную в этом интервале. Функция
, имеющих скорость, заключенную в этом интервале. Функция  определяет относительное число молекул
определяет относительное число молекул  , скорости которых лежат в интервале от
, скорости которых лежат в интервале от  до
до  , т. е.
, т. е.
 , откуда
, откуда  .
.
Применяя методы теории вероятностей, Максвелл нашел вид этой функции:
 ,
,
где 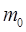 – масса одной молекулы газа.
– масса одной молекулы газа.
График этой функции приведен на рис. 2.

Рис. 2
Относительное число молекул  , скорости которых лежат в интервале от
, скорости которых лежат в интервале от  до
до  , соответствует площади заштрихованной на рис. 2 полоски. Площадь под всей кривой распределения
, соответствует площади заштрихованной на рис. 2 полоски. Площадь под всей кривой распределения  равна единице. Это означает, что функция
равна единице. Это означает, что функция  удовлетворяет условию нормировки:
удовлетворяет условию нормировки:
 .
.
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью  :
:
 .
.
Из этой формулы следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 3) смещается вправо. При этом величина максимума функции распределения молекул по скоростям  с повышением температуры уменьшается (рис. 3).
с повышением температуры уменьшается (рис. 3).

Рис. 3
Кроме наиболее вероятной скорости  , на рис. 2 приведены также средняя арифметическая скоростьмолекул
, на рис. 2 приведены также средняя арифметическая скоростьмолекул  и средняя квадратичная скоростьмолекул
и средняя квадратичная скоростьмолекул  , которые определяются по формулам:
, которые определяются по формулам:
 ;
;  .
.
Дата добавления: 2014-12-23; просмотров: 326; Мы поможем в написании вашей работы!; Нарушение авторских прав |