
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистические методы анализа динамики социально-экономических явлений
Цель: сформировать знания о методах обработки динамических данных, способах расчета обобщающих характеристик рядов динамики, методах выявления трендов и циклов, методах моделирования и прогнозирования развития социально-экономических процессов.
Задачи: раскрыть понятие ряда динамики, их видов, элементов динамического ряда; представить основные показатели рядов динамики; обобщить основные методы выявления трендов и циклов; показать основные принципы моделирования и прогнозирования.
Понятие и классификация рядов динамики
Под динамикой в статистике понимается процесс развития некоторого явления во времени. Задачи оценки и выявления закономерностей развития изучаемого явления/процесса во времени предполагают необходимость статистического анализа рядов динамики.
Ряд динамики (временной ряд, хронологический ряд) – это ряд значений изучаемого показателя, изменяющихся во времени и расположенных в хронологическом порядке. Каждый ряд динамики состоит из двух элементов: уровня ряда и показателя времени.
Уровень рядадинамики, 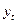 - это отдельное числовое значение статистического показателя, являющегося количественной оценкой изучаемого явления во времени, т.е. за отдельный период или на определенный момент времени.
- это отдельное числовое значение статистического показателя, являющегося количественной оценкой изучаемого явления во времени, т.е. за отдельный период или на определенный момент времени.
Показатель времениряда динамики, 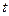 - это определенные моменты (даты) или периоды (годы, месяцы и т.п.) времени, для которых зафиксированы значения уровней ряда динамики.
- это определенные моменты (даты) или периоды (годы, месяцы и т.п.) времени, для которых зафиксированы значения уровней ряда динамики.
В зависимости от вида показателя различают ряды абсолютных, относительных и средних величин. В табл. 5.1 приведены ряды динамики указанных видов.
Таблица 5.1
Число и средний размер квартир, построенных населением за счет собственных и заемных средств1
| Год | ||||
| Число квартир, тыс. | ||||
| Средний размер квартир, м2 общей площади | 138,5 | 138,3 | 138,7 | 138,7 |
| Удельный вес в общем вводе, % | 39,2 | 40,2 | 39,5 | 42,8 |
1) по материалам статистического сборника «Социальное положение и уровень жизни населения России. 2008»
В зависимости от показателя времени различают моментные и интервальные ряды динамики. Это деление соответствует двум разным типам величин, составляющих ряд динамики: величин типа потока и величин типа запаса.
Моментный ряд динамики – это ряд, уровни которого отражают состояние изучаемого явления на определенные моменты времени (численность сотрудников на конец года, остаток денежных средств на начало месяца, запас сырья на конец смены и т.п.).
Интервальный (периодический) ряд динамики – это ряд, уровни которого характеризуют величину изучаемого явления за определенные интервалы (периоды) времени (производство продукции в месяц, доходы за год, квартальные затраты и т.п.).
В табл. 5.2 представлен моментный ряд динамики. Все три ряда динамики, приведенные в табл. 5.1, являются интервальными.
Таблица 5.2
Численность работников государственных органов и органов местного самоуправления на конец года1
| Численность работников, тыс. чел. |
1) по материалам статистического сборника «Российский статистический ежегодник. 2009»
В зависимости от временных расстояний между уровнями различают полные и неполные ряды динамики.
В полных рядах динамики уровни ряда являются равноотстоящими, т.е. значения показателя времени следуют через определенные промежутки (для моментных рядов) или следуют друг за другом (для интервальных рядов).
В неполных рядах динамики уровни ряда являются неравноотстоящими, т.е. значения показателя времени соответствуют неравномерным промежуткам между моментами или прерывающимся периодам.
Данные табл. 5.1 представляют собой полные ряды, в табл. 5.2 приведен неполный ряд динамики.
В зависимости от наличия определенной тенденции в исследуемом процессе ряды динамики могут быть стационарными и нестационарными.
В стационарных рядах динамики основные характеристики случайного процесса (математическое ожидание и дисперсия) постоянны; в нестационарных рядах динамики - зависят от времени.
Сопоставимость уровней и смыкание рядов динамики
Основным условием правильного построения и последующего анализа ряда динамики является сопоставимость всех уровней ряда. При этом на сопоставимость оказывают влияние множество условий.
Так, должна быть произведена периодизация динамики, т.е. выделение из всего процесса однородных этапов развития. Фактически, периодизация динамики представляет собой типологическую группировку по времени, целью которой является получение однородных, однокачественных временных периодов. При этом понятие однородности относительно и определяется целью исследования.
Показатель времени ряда динамики должен соответствовать интенсивности изучаемого процесса. Это значит, что при большой вариации уровней ряда динамики значения показателей должны регистрироваться с меньшими интервалами, чем при изучении стабильных процессов.
Достоверность данных рядов динамики и отсутствие пропусков отдельных уровней также влияет на итоговые результаты анализа.
Важнейшим требованием является сопоставимость статистических данных, составляющих уровни ряда динамики, которая должна быть обеспечена по следующим позициям:
1. по содержанию (показатели должны быть определены однозначно для всех моментов/периодов времени);
2. по кругу охватываемых объектов (так как ряд объектов со временем может переходить из одной категории в другую);
3. по методологии расчета (показатели должны быть расчитаны по одной и той же методике расчета для всех моментов/периодов времени);
4. по единицам измерения или счета (например, при изменении масштаба цен все статистические данные должны быть пересчитаны в новый масштаб);
5. по территориальным границам (при наличии изменений все данные должны быть пересчитаны с учетом новых границ стран, областей, районов и т.п.);
6. по времени регистрации (если на измеряемые показатели оказывает влияние сезонность, уровни моментного ряда должны относиться к одинаковым датам).
При несоблюдении в данных динамики вышеназванных условий для достижения сопоставимости используют различные приемы: прямого пересчета, смыкания рядов динамики, приведения к одному основанию.
Прямой пересчет заключается в корректировке первичных данных при обнаружении их несопоставимости по кругу объектов или территориальных границ.
При отсутствии данных, необходимых для прямого пересчета, используется прием смыкания рядов динамики, который заключается в объединении в один двух или нескольких рядов, исчисленных по разным методикам или разным территориальным границам. Для применения этого метода необходимо наличие для переходных периодов/моментов данных, исчисленных по разным методикам или в разных границах. Смыкание рядов динамики может быть произведено двумя способами.
Первый основан на расчете коэффициента соотношения уровней переходного периода/момента, рассчитанных по старой и новой методикам. Все данные за предшествующие изменению периоды/моменты времени пересчитываются путем умножения на данный коэффициент:

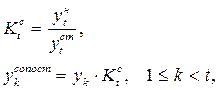
где 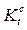 - коэффициент соотношения уровней ряда для периода/момента t, в который произошло изменение методологии расчета;
- коэффициент соотношения уровней ряда для периода/момента t, в который произошло изменение методологии расчета;
 ,
, 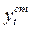 - уровни ряда динамики, относящиеся к одному периоду/моменты времени и исчисленные по старой и новой методике соответственно;
- уровни ряда динамики, относящиеся к одному периоду/моменты времени и исчисленные по старой и новой методике соответственно;
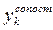 - условно-сопоставимый уровень для периода/момента k;
- условно-сопоставимый уровень для периода/момента k;
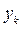 - несопоставимый уровень для периода/момента k.
- несопоставимый уровень для периода/момента k.
В результате ряды смыкаются и уровни вновь образованного ряда оказываются условно сопоставимыми.
Второй способ смыкания рядов динамики заключается в переходе от абсолютных величин к относительным. Для этого уровни ряда в переходный период/момент, рассчитанные по разным методикам принимаются за 100%, а остальные пересчитываются в процентах по отношению к ним соответственно своему ряду.
В табл. 5.3 на условном примере приведена иллюстрация обоих способов смыкания рядов динамики. Данные свидетельствуют о том, что в 2007 году произошло изменение границ района. Для получения сопоставимых данных необходимо объединить два ряда динамики.
По первому способу смыкания был рассчитан коэффициент соотношения уровней  . Затем, путем умножения на данный коэффициент, были пересчитаны данные в старых границах. В результате был получен сомкнутый сопоставимый ряд абсолютных величин численности населения в новых границах.
. Затем, путем умножения на данный коэффициент, были пересчитаны данные в старых границах. В результате был получен сомкнутый сопоставимый ряд абсолютных величин численности населения в новых границах.
Для перехода к сомкнутому сопоставимому ряду динамики по второму способу для каждого ряда (в старых и новых границах) были пересчитаны абсолютные значения численностей в проценты к 2007 году. Например, 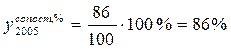 ,
, 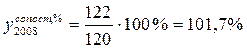 .
.
Таблица 5.3
Динамика численности населения административного округа (цифры условные)
| Год | |||||
| Численность населения, тыс. чел.: | |||||
| в старых границах района | - | - | |||
| в новых границах района | - | - | |||
| Численность населения в новых границах района, тыс. чел (сомкнутый ряд) | 103,2 | 112,8 | |||
| Численность населения, % к 2007 г. (сомкнутый ряд) | 86,0 | 94,0 | 100,0 | 101,7 | 103,3 |
При проведении сравнительного анализа динамики определенных показателей для разных совокупностей (например, для разных территориальных районов, стран и т.п.) также возникает проблема сопоставимости, для решения которой используется метод приведения к одному снованию. Суть метода заключается в переходе к относительным величинам, значения которых определяются в коэффициентах или процентах по отношению к периоду/моменту, выбранному за базу сравнения (одинаковому всех для сравниваемых совокупностей). В результате несопоставимость, присущая уровням, выраженным в абсолютных величинах, нивелируется.
Метод приведения к одному основанию проиллюстрирован в табл. 5.4. Необходимость применения данного метода обусловлена различиями в методологии учета безработных в двух странах. За постоянную базу сравнения принят 2003 год. Затем осуществлен переход к относительным величинам численности безработных по каждой стране. Эти величины характеризуют рост/снижение численности безработных по отношению к 2003 году.
Таблица 5.4
Общая численность безработных на конец года1
| Год | |||||
| Численность безработных, тыс. чел.: | |||||
| Россия | |||||
| Германия | |||||
| Численность безработных, % к 2003 году (сопоставимые данные): | |||||
| Россия | 100,0 | 101,6 | 91,6 | 88,0 | 74,7 |
| Германия | 100,0 | 109,1 | 113,9 | 106,4 | 89,7 |
1) по материалам статистического сборника «Российский статистический ежегодник. 2009»
Показатели изменения уровней рядов динамики. Сводные показатели динамики
Для анализа скорости и интенсивности развития динамических процессов применяется целый комплекс статистических показателей динамики, которые подразделяются на индивидуальные и сводные показатели динамики.
Индивидуальные показатели динамики основаны на сравнении уровней ряда между собой. Сравниваемый уровень называют текущим, а тот, с которым производится сравнение, - базисным. При этом могут различаться как база сравнения, так и форма сопоставления уровней. В зависимости от того, какой уровень ряда выбран за базу, различают базисные показатели и цепные.
Если сравнение всех уровней происходит с одним и тем же уровнем, взятым за базу, результатом будут базисные показатели динамики, или показатели с постоянной базой сравнения. В качестве постоянной базы сравнения обычно используют начальный уровень ряда. Однако, такой базой может быть и средний уровень какого-либо предшествующего периода, и эталонный уровень определенного момента/периода…
Если уровни ряда последовательно сравниваются с предыдущими (по времени), то в результате получают набор цепных показателей динамики, или показателей с переменной базой сравнения.
В зависимости от формы сопоставления различают следующие показатели: абсолютный прирост, коэффициент или темп роста, коэффициент или темп прироста, абсолютное и относительное ускорение, абсолютное значение одного процента прироста.
Абсолютный прирост, цепной  и базисный
и базисный 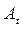 - это разность между текущим уровнем ряда и базисным (предыдущим и начальным, соответственно):
- это разность между текущим уровнем ряда и базисным (предыдущим и начальным, соответственно):
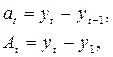
где 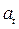 – цепной абсолютный прирост;
– цепной абсолютный прирост;
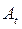 - базисный абсолютный прирост;
- базисный абсолютный прирост;
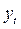 - уровень ряда в момент/период t;
- уровень ряда в момент/период t;
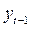 - уровень ряда в предыдущий момент/период;
- уровень ряда в предыдущий момент/период;
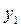 - уровень ряда в начальный момент/период.
- уровень ряда в начальный момент/период.
Абсолютный прирост может быть как положительным, так и отрицательным. При этом он показывает, на сколько единиц, соответственно, увеличился или уменьшился текущий уровень ряда динамики по сравнению с базисным. Отрицательное значение этого показателя называют абсолютным сокращением. Выражая абсолютную скорость изменения, данный показатель имеет ту же размерность, что и уровни ряда.
Можно показать, что сумма последовательных цепных абсолютных приростов равна базисному абсолютному приросту за соответствующий промежуток времени:
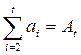 .
.
Коэффициент роста, цепной 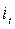 и базисный
и базисный 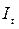 - это отношение текущего уровня ряда к базисному (предыдущему и начальному, соответственно):
- это отношение текущего уровня ряда к базисному (предыдущему и начальному, соответственно):
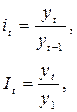
где 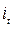 – цепной коэффициент роста;
– цепной коэффициент роста;
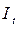 - базисный коэффициент роста.
- базисный коэффициент роста.
Коэффициент роста всегда положителен и показывает, во сколько раз текущий уровень больше базисного (если значение коэффициента больше единицы) или какую часть базисного уровня составляет текущий (если значение коэффициент меньше единицы). Таким образом, если коэффициент роста больше единицы, значит, текущий уровень вырос по сравнению с базисным; если равен единице – не изменился; если меньше единицы - снизился. Выражая относительную интенсивность изменения, данный показатель является величиной безразмерной.
Можно показать, что произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за соответствующий промежуток времени:
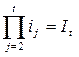 .
.
Темп роста, цепной 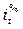 и базисный
и базисный 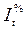 – это коэффициент роста, выраженный в процентах:
– это коэффициент роста, выраженный в процентах:

Темп роста отличается от коэффициента роста только единицами измерения и показывает, сколько процентов составляет текущий уровень от базисного. Темп роста всегда положителен. При этом, если темп роста больше 100%, значит, текущий уровень вырос по сравнению с базисным; если равен 100% – не изменился; если меньше 100% - снизился.
Коэффициент прироста, цепной 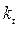 и базисный
и базисный 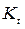 - это отношение абсолютного прироста (цепного и базисного, соответственно) к базисному уровню ряда (предыдущему и начальному, соответственно):
- это отношение абсолютного прироста (цепного и базисного, соответственно) к базисному уровню ряда (предыдущему и начальному, соответственно):
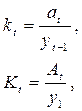
где 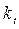 – цепной коэффициент прироста;
– цепной коэффициент прироста; 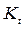 - базисный коэффициент прироста.
- базисный коэффициент прироста.
Коэффициент прироста может быть как положительным, так и отрицательным. При этом он показывает, на какую долю, соответственно, увеличился или уменьшился текущий уровень по сравнению с базисным. Выражая относительную скорость изменения, данный показатель является величиной безразмерной.
Можно показать, что коэффициент прироста непосредственно связан с коэффициентом роста:

 .
.
Темп прироста, цепной 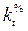 и базисный
и базисный 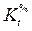 – это коэффициент прироста, выраженный в процентах:
– это коэффициент прироста, выраженный в процентах:
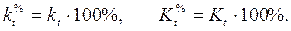
Как и коэффициент прироста, темп прироста может быть положительным или отрицательным. При этом он показывает, на какой процент текущий уровень, соответственно, увеличился или уменьшился по сравнению с базисным.
Темп прироста связан с темпом роста следующим образом:
 .
.
Если уровни ряда динамики могут принимать положительные и отрицательные значения (например, показатель прибыли/убытка), то коэффициенты/темпы роста и прироста не рассчитываются, так как не могут быть интерпретированы.
Абсолютное ускорение, 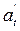 - это разность двух последовательных цепных абсолютных приростов:
- это разность двух последовательных цепных абсолютных приростов:
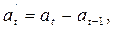
где 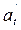 – абсолютное ускорение.
– абсолютное ускорение.
Абсолютное ускорение может быть положительным и отрицательным и показывает, на сколько текущая скорость изменения, соответственно, больше или меньше предыдущей. Отрицательные значения абсолютного ускорения интерпретируют как замедление роста или как ускорение снижения уровней ряда. Выражая абсолютную скорость изменения скорости, этот показатель имеет ту же размерность, что и уровни ряда.
Относительное ускорение, 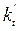 - это отношение абсолютного ускорения к цепному абсолютному приросту, взятому за базу:
- это отношение абсолютного ускорения к цепному абсолютному приросту, взятому за базу:
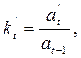
где  – относительное ускорение.
– относительное ускорение.
Относительное ускорение может быть как положительным, так и отрицательным, в зависимости от знака абсолютного ускорения. Однако, для возможности расчета относительного ускорения абсолютный прирост, взятый за базу сравнения, должен быть положительным. Выражая относительную скорость изменения абсолютной скорости, данный показатель является величиной безразмерной. Как и коэффициент прироста, относительное ускорение может быть выражено в процентах.
Таблица 5.5
Общая площадь приватизированных жилых помещений, млн. м2
| Годы | Млн. м2 | По сравнению с 2004 г. | ||
| Абсолютный прирост, млн. м2 | Темп роста, % | Темп прироста, % | ||
| - | 100,0 | - | ||
| 129,0 | 29,0 | |||
| 113,0 | 13,0 | |||
| -33 | 52,2 | -47,8 | ||
| -38 | 44,9 | -55,1 | ||
| ИТОГО | - | - | - |
| Годы | Млн. м2 | По сравнению с предыдущим годом | Абсолютное значение одного процента прироста, млн. м2 | ||
| Абсолютный прирост, млн. м2 | Темп роста, % | Темп прироста, % | |||
| - | - | - | - | ||
| 129,0 | 29,0 | 0,69 | |||
| -11 | 87,6 | -12,4 | 0,89 | ||
| -42 | 46,2 | -53,8 | 0,78 | ||
| -5 | 86,1 | -13,9 | 0,36 | ||
| ИТОГО | -38 | - | - | - |
1) по материалам статистического сборника «Российский статистический ежегодник. 2009»
Абсолютное значение одного процента прироста,  - это отношение цепного абсолютного прироста к соответствующему цепному темпу прироста и в то же время – сотая часть базисного уровня:
- это отношение цепного абсолютного прироста к соответствующему цепному темпу прироста и в то же время – сотая часть базисного уровня:
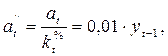
где 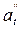 – абсолютное значение одного процента прироста.
– абсолютное значение одного процента прироста.
Данный показатель выражает абсолютное значение, приходящееся на один процент прироста, и измеряется в тех же единицах, что и уровни ряда.
В табл. 5.5 произведен расчет индивидуальных показателей динамики.
Сводные показатели ряда динамики являются обобщающими показателями, рассчитываемыми по всему ряду динамики. К сводным показателям относятся средний уровень ряда динамики и средние показатели изменения уровней ряда.
Средний уровень ряда динамики – это обобщающая характеристика изменяющегося во времени показателя, представляющая его среднее значение, которое рассчитывается по формуле средней хронологической. По данной формуле рассчитываются средние уровни для рядов динамики абсолютных и средних величин.
Для интервальных и моментных рядов динамики методика расчета среднего уровня различается.
Для потоковых величин, составляющих интервальный ряд динамики, средний уровень представляет по сути среднюю интенсивность потока, определяемую как средняя арифметическая. Если при этом ряд динамики состоит из равноотстоящих уровней, то используется средняя арифметическая простая; если из неравноотстоящих – средняя арифметическая взвешенная:
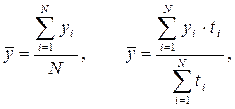
где  - средний уровень интервального ряда динамики;
- средний уровень интервального ряда динамики;
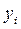 - уровень ряда в i – й период;
- уровень ряда в i – й период;
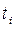 - продолжительность i – го периода;
- продолжительность i – го периода;
 - число уровней.
- число уровней.
Интервальный ряд может быть более или менее подробным, но если в периодах нет пропусков, он всегда полный. Моментный же ряд неполон в принципе и представляет собой всегда выборочное описание процесса. Так как отдельные уровни моментного ряда содержат элементы повторного счета, используется другой подход к определению среднего уровня – расчет средней хронологической, в простой форме – для ряда с равноотстоящими моментами времени и в взвешенной форме – для неравноотстоящих уровней:
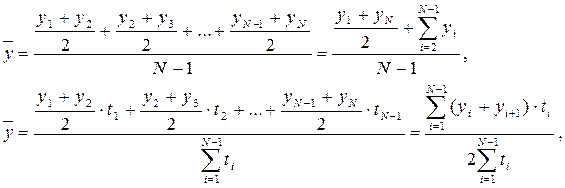
где  - средний уровень моментного ряда динамики;
- средний уровень моментного ряда динамики;
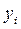 - уровень ряда в i – й момент;
- уровень ряда в i – й момент;
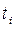 - продолжительность интервала между i – м и (i+1) – м моментами;
- продолжительность интервала между i – м и (i+1) – м моментами;
 - число уровней.
- число уровней.
В табл. 5.5 представлен интервальный ряд динамики с равноотстоящими уровнями. Среднегодовая общая площадь приватизированных помещений за 2004-2008 гг. будет следующей:
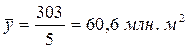 .
.
Данные табл. 5.4 представляют собой моментные ряды динамики с равноотстоящими уровнями. Согласно этим данным среднегодовая численность безработных в России на период 2004-2008 гг. составляла:
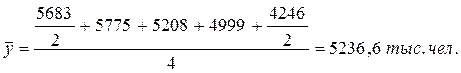
В табл. 5.2 представлен также моментный ряд динамики, однако, его уровни не являются равноотстоящими. Средняя численность работников государственных органов и органов местного самоуправления составляет:


Средние показатели изменения уровней ряда рассчитываются путем усреднения индивидуальных показателей динамики, получая средний абсолютный прирост, средний коэффициент/темп роста, средний коэффициент/темп прироста. Усреднению подлежат только цепные показатели динамики. При этом предполагается, что все они исчислены за одинаковые промежутки времени.
Средний абсолютный прирост, 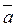 - обобщающий показатель, характеризующий среднюю абсолютную скорость изменения (роста/снижения). Ведущий показатель при этом определяется, исходя из условия: если уровень ряда будет последовательно расти (снижаться) на
- обобщающий показатель, характеризующий среднюю абсолютную скорость изменения (роста/снижения). Ведущий показатель при этом определяется, исходя из условия: если уровень ряда будет последовательно расти (снижаться) на 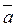 в единицу времени, то начиная с первого уровня, за то же число периодов достигнет конечного. Этому условию отвечает показатель, равный сумме последовательных цепных абсолютных приростов, т.е. базисный абсолютный прирост. Таким образом, средний абсолютный прирост определяется как среднее арифметическое из цепных абсолютных приростов:
в единицу времени, то начиная с первого уровня, за то же число периодов достигнет конечного. Этому условию отвечает показатель, равный сумме последовательных цепных абсолютных приростов, т.е. базисный абсолютный прирост. Таким образом, средний абсолютный прирост определяется как среднее арифметическое из цепных абсолютных приростов:
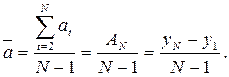
Средний абсолютный прирост показывает, на сколько в среднем увеличивался или уменьшался уровень ряда по сравнению с предыдущим за единицу времени за весь анализируемый период.
Средний коэффициент роста, 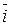 - обобщающий показатель, характеризующий среднюю интенсивность изменения. То есть, это такой показатель, что если в единицу времени уровень ряда будет последовательно расти (снижаться) в
- обобщающий показатель, характеризующий среднюю интенсивность изменения. То есть, это такой показатель, что если в единицу времени уровень ряда будет последовательно расти (снижаться) в 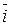 раз в единицу времени, то начиная с первого уровня, за то же число периодов достигнет конечного. Ведущий показатель в данном случае представляет собой произведение цепных коэффициентов роста, т.е. базисный коэффициент роста. Таким образом, средний коэффициент роста определяется как среднее геометрическое из цепных коэффициентов роста:
раз в единицу времени, то начиная с первого уровня, за то же число периодов достигнет конечного. Ведущий показатель в данном случае представляет собой произведение цепных коэффициентов роста, т.е. базисный коэффициент роста. Таким образом, средний коэффициент роста определяется как среднее геометрическое из цепных коэффициентов роста:
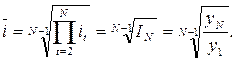
Средний коэффициент роста показывает, во сколько раз в среднем изменялся уровень ряда динамики по сравнению с предыдущим за единицу времени за весь анализируемый период.
Средний темп роста, 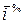 - это средний коэффициент роста, выраженный в процентах:
- это средний коэффициент роста, выраженный в процентах:
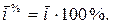
Средний темп роста показывает, сколько процентов в среднем за единицу времени составлял уровень ряда динамики от предыдущего за весь анализируемый период.
Средний коэффициент прироста, 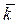 - обобщающий показатель, характеризующий среднюю относительную скорость изменения. Данный показатель не определяется непосредственным усреднением цепных коэффициентов прироста, а находится через средний коэффициент роста:
- обобщающий показатель, характеризующий среднюю относительную скорость изменения. Данный показатель не определяется непосредственным усреднением цепных коэффициентов прироста, а находится через средний коэффициент роста:
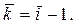
Средний коэффициент прироста показывает, на какую долю в среднем изменялся уровень ряда динамики по сравнению с предыдущим за единицу времени за весь анализируемый период.
Средний темп прироста,  - это средний коэффициент прироста, выраженный в процентах:
- это средний коэффициент прироста, выраженный в процентах:
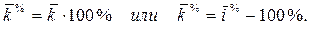
Средний темп прироста показывает, на сколько процентов в среднем изменялся уровень ряда динамики по сравнению с предыдущим за единицу времени за весь анализируемый период.
Средние показатели изменения уровней ряда, представленного в табл. 5.5, будут следующими.
Средний абсолютный прирост:
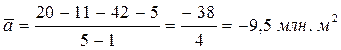 ,
,
т.е. в период 2004-2008 гг. общая площадь приватизируемых помещений сокращалась ежегодно в среднем на 9,5 млн. м2.
Средний коэффициент и темп роста:
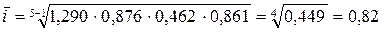 ,
,
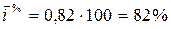 ,
,
т.е. в период 2004-2008 гг. годовая общая площадь приватизируемых помещений сокращалась и составляла в среднем 0,82 от общей площади помещений, приватизированных в предыдущем году, или 82%.
Средний коэффициент и темп прироста:
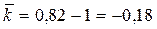 ,
,
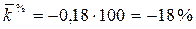 ,
,
т.е. в период 2004-2008 гг. годовая общая площадь приватизируемых помещений сокращалась в среднем на 0,18 от общей площади помещений, приватизированных в предыдущем году, или на 18%.
Компоненты ряда динамики. Методы выравнивания ряда динамики
Исследование рядов динамики не ограничивается изучением скорости и интенсивности развития динамических процессов с помощью системы показателей. Большой интерес представляет изучение закономерностей изменения уровней ряда во времени.
На ряд динамики могут воздействовать факторы эволюционного, осциллятивного и случайного характера.
Общее направление развития (эволюция) динамического процесса определяется факторами эволюционного характера, действующими на ряд динамики практически постоянно. При этом об изменениях значений уровней ряда говорят как о тенденции развития.
Основная тенденция развития, или тренд, - это общее направление развития (рост, снижение или стабилизация) процесса с течением времени.
Факторы осциллятивного характера, действуя на ряд динамики периодически и кратковременно, вызывают, соответственно, циклические (конъюнктурные) и сезонные колебания.
Циклические (конъюнктурные) колебания – это долговременные регулярные колебания, вызванные постоянно действующими факторами (например, циклы экономической конъюнктуры). Их воздействие схематически походит на синусоиду: значение признака за определенное время достигает максимума, затем – минимума, потом вновь возрастает и т.д.
Сезонные колебания – это периодические колебания, повторяющиеся в определенное время года, дни месяца, часы суток.
Факторы случайного характера, действуя несистематически, вызывают нерегулярные колебания то в одном, то в другом направлении. Эти явления делят две группы: вызывающие спорадические (война, экологическая катастрофа) и случайные, второстепенные изменения.
Исходя из вышеописанной классификации факторов, воздействующих на динамические процессы, для целей анализа в рядах динамики выделяют четыре основные компоненты:
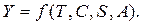
Компоненты ряда динамики связаны между собой. В зависимости от характера этой взаимосвязи различают аддитивную и мультипликативную модели рядов динамики.
Для аддитивной модели вида 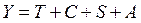 характерны постоянные амплитуды циклических и сезонных колебаний на протяжении всего ряда динамики.
характерны постоянные амплитуды циклических и сезонных колебаний на протяжении всего ряда динамики.
В мультипликативной модели вида 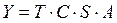 циклические и сезонные колебания образуются с переменной амплитудой.
циклические и сезонные колебания образуются с переменной амплитудой.
Построение модели динамического процесса сводится к его «разложению» на компоненты с расчетом их значений для каждого уровня ряда динамики.
Методы выявление основной тенденции в рядах динамики
Под колеблемостью в динамических рядах понимаются отклонения уровней ряда от основной тенденции (тренда).
Тренд – это компонента ряда динамики, характеризующая основную долговременную тенденцию изменения его уровней. Обычно тренд описывают гладкой функцией.
Для описания тенденции используют методы механического и аналитического выравнивания.
Суть методов механического выравнивания заключается в замене фактических уровней ряда расчетными, для которых характерна меньшая степень колеблемости. К данным методам относятся методы: усреднения по левой и правой половине, укрупнения интервалов, скользящих средних.
Метод усреднения по левой и правой половине подразумевает разделение ряда на две равные части с последующим расчетом средних уровней для каждой половины. Через рассчитанные средние значения проводится прямая, характеризующая линию тренда на графике. Данный метод очень грубый и позволяет описать тренд только уравнением прямой.
Метод укрупнения интервалов заключается в замене ряда динамики другим, уровни которого относятся к более продолжительным периодам времени. Переход к новым значениям признака для более продолжительных периодов осуществляется либо путем суммирования, либо через усреднение уровней предыдущего ряда. Если уровни колеблются с определенной периодичностью, то для устранения влияния таких колебаний укрупненный интервал желательно взять равным длине «волны». Данный метод позволяет более четко «разглядеть» основную тенденцию в изучаемом процессе.
Метод скользящей средней заключается в последовательном (со сдвигом на один уровень) объединении внутри ряда динамики нескольких уровней и расчете для таких локальных периодов их средних уровней.
Интервал сглаживания – это целое число уровней, которые объединяются в локальный период и для которых рассчитывается средний уровень. Интервал сглаживания может быть нечетным и четным.
Звено скользящей средней – это средний уровень за выбранный интервал сглаживания. Каждое звено скользящей средней относят к середине локального периода.
Для нечетного интервала сглаживания значения скользящей средней определяются по формуле:
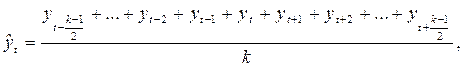
где 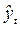 - выровненный уровень (скользящее среднее);
- выровненный уровень (скользящее среднее);
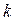 - интервал сглаживания (нечетный).
- интервал сглаживания (нечетный).
При четном интервале сглаживания каждое звено скользящей средней должно относиться к середине между центральными датами локального интервала. Для ликвидации такого сдвига применяют способ центрирования. Он заключается в усреднении смежных звеньев скользящей средней и отнесении полученного результата к определенной дате (середине между смежными звеньями).
Использование метода скользящей средней позволяет сгладить ряд с сильными колебаниями. Необходимо отметить, что с увеличением интервала увеличивается и эффект сглаживания, но при этом растет и число «потерянных» значений, т.е. ряд укорачивается на 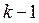 значений.
значений.
Также к недостаткам метода можно отнести отсутствие аналитического выражения для основной тенденции, что неудобно для целей прогнозирования. Вместе с тем, метод скользящей средней широко используется на первом этапе построения моделей динамики.
В табл. 5.6 приведены исходные и расчетные данные, иллюстрирующие методы механического выравнивания.
Графики исходных данных и выровненных рядов представлены на рис. 5.1.
Таблица 5.6
Динамика объема продаж условного товара за 1995-2009 гг. и механическое выравнивание уровней
| № уровня | Год | Объем продаж, млн. шт./год | Средняя за пять лет | Скользящая средняя (интервал 3 года) | Скользящая средняя (интервал 5 лет) |
| 4,0 | - | - | |||
| 3,0 | - | ||||
| 3,3 | 4,0 | ||||
| 5,3 | 5,2 | ||||
| 6,0 | 5,6 | ||||
| 11,2 | 7,0 | 7,4 | |||
| 8,7 | 9,4 | ||||
| 10,3 | 11,2 | ||||
| 14,7 | 12,4 | ||||
| 14,3 | 16,4 | ||||
| 24,2 | 18,7 | 18,4 | |||
| 20,7 | 22,0 | ||||
| 26,3 | 24,2 | ||||
| 27,7 | - | ||||
| - | - |
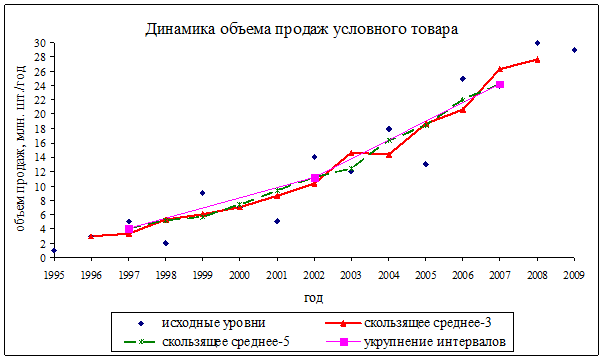
Рис. 5.1. Динамика объема продаж условного товара. Механическое выравнивание.
Видно, что изначально сильно варьирующие данные после выравнивания проявляют более четкую тенденцию. В методе скользящей средней выравнивание тем больше, чем больше интервал сглаживания, однако, это сопровождается потерей большего количества уровней.
Метод аналитического выравнивания состоит в подборе функции 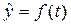 для описания зависимости уровней ряда от времени, которая в определенном отношении была бы наиболее близка к фактическим значениям уровней ряда динамики.
для описания зависимости уровней ряда от времени, которая в определенном отношении была бы наиболее близка к фактическим значениям уровней ряда динамики.
Аналитическое выравнивание подразумевает последовательную реализацию трех этапов: подбор вида аналитического уравнения (т.е. формы кривой), расчет параметров выбранной функции, расчет теоретических (т.е. по модели) значений уровней ряда и анализ полученной модели.
Вид уравнения тренда определяется сущностью исследуемого процесса. На практике такой подбор чаще всего основывается на графическом анализе фактических уровней ряда динамики или их сглаженных значений. При этом могут использоваться различные уравнения: полиномы разной степени, логистические кривые, экспоненты и др.
Если основная тенденция хорошо описывается несколькими видами функций, выбирают более простую. Это непосредственно связано с надежностью оцениваемых параметров, так как с увеличением количества параметров уравнения эта надежность снижается и, одновременно, растут ошибки оценки параметров функции и будущих прогнозов.
При выборе вида функции может использоваться метод конечных разностей. Для применения данного метода уровни ряда должны быть равноотстоящими.
Разности первого порядка представляют собой цепные абсолютные приросты:
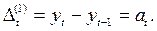
Разности второго порядка равны разности между текущим и предыдущим значениями разностей первого порядка, т.е. представляют собой абсолютные ускорения:
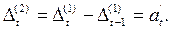
Разности j-го порядка равны разности между текущим и предыдущим значениями разностей (j-1)-го порядка:
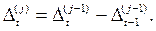
Анализ конечных разностей позволяет выбрать степень полинома в соответствующей модели динамики:
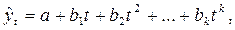
где 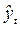 - выровненный уровень (теоретическое значение);
- выровненный уровень (теоретическое значение);
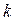 - степень полинома.
- степень полинома.
При постоянстве разностей j-го порядка рекомендуется использовать полином j-й степени. Преимущество полиномов невысоких степеней состоит в возможности конкретной интерпретации их параметров. Параметр 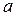 характеризует средние условия образования уровней ряда динамики, а параметры
характеризует средние условия образования уровней ряда динамики, а параметры 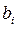 - изменения ускорения.
- изменения ускорения.
Таким образом, если разности первого порядка приблизительно равны друг другу, это свидетельствует о том, что уровни ряда изменяются приблизительно в арифметической прогрессии. В данном случае рекомендуется полином первой степени, т.е. прямая:

Линейный характер динамики встречается довольно часто. Параметр 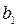 называется коэффициентом регрессии и интерпретируется как средний абсолютный прирост за единицу времени, т.е. показывает, на сколько в среднем изменится уровень ряда при изменении времени на единицу. Знак коэффициента регрессии определяет направление развития: при
называется коэффициентом регрессии и интерпретируется как средний абсолютный прирост за единицу времени, т.е. показывает, на сколько в среднем изменится уровень ряда при изменении времени на единицу. Знак коэффициента регрессии определяет направление развития: при 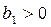 - к равномерному росту, при
- к равномерному росту, при 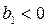 - к равномерному снижению.
- к равномерному снижению.
Если примерно постоянны разности второго порядка (ускорения), то рекомендуется полином (парабола) второй степени:
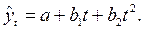
Парабола второго порядка хорошо описывает динамические процессы, для которых характерно изменение направления развития: со снижения - к росту, и наоборот. При этом  выражает начальную скорость роста, а
выражает начальную скорость роста, а 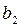 - постоянную скорость изменения прироста (абсолютное ускорение).
- постоянную скорость изменения прироста (абсолютное ускорение).
Теоретически любой ряд динамики может быть абсолютно точно описан полиномом. Однако, параболы выше третьего порядка на практике не используются не только из-за снижения надежности оценок параметров, но и из-за нивелирования сути тренда как отражения основной тенденции: парабола, проходящая через все точки ряда динамики смешивает основную тенденцию с колебаниями.
Кроме метода конечных разностей, для выбора конкретного вида функции используют анализ самого процесса.
Если цепные коэффициенты роста оказываются примерно одинаковыми, это свидетельствует об изменении уровней согласно геометрической прогрессии. В данном случае выравнивание можно произвести по показательной и экспоненциальной функции:
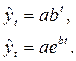
Экспоненциальный характер основной тенденции свойственен процессам, потенциально не имеющим ограничений для роста. Но на практике это возможно лишь на ограниченном промежутке времени. Параметр 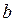 (
( 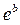 ) в данных моделях интерпретируется как средний коэффициент роста.
) в данных моделях интерпретируется как средний коэффициент роста.
Для убывающих процессов, в которых значения исследуемого признака стремятся, но не могут достичь, с одной стороны нуля, с другой – некоторого предела, используется гиперболическая функция:
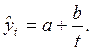
Для процессов, проходящих полный цикл развития: возрастание с ускорением в начале, стабилизация в середине и затухание в конце при приближении к предельному уровню, - применяют логистическую функцию.
Расчет параметров выбранной функции тренда может производиться различными способами: по известным уровням ряда динамики, методом линейных отклонений, методом конечных разностей, методом наименьших квадратов. Первые два метода могут применяться лишь для ориентировочных расчетов.
Чаще всего на практике используется метод наименьших квадратов, предполагающий определение параметров выбранной функции, при которых сумма квадратов отклонений фактических уровней ряда динамики от соответствующих по времени выровненных уровней будет минимальна:
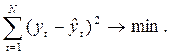
Параметры функции, удовлетворяющие данному условию, находятся решением системы нормальных уравнений. При этом вид системы уравнений и, соответственно, ее решение значительно упрощается, если исходную временную шкалу, представленную рядом натуральных чисел (1,2,…), заменить преобразованной, для которой сумма показателей времени равна нулю.
Переход к новой шкале при нечетном числе уровней ряда осуществляется переносом начала отсчета времени (нуля) в середину, приписывая его центральному уровню ряда:
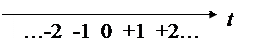
При четном числе уровней ряда начало отсчета времени находится между двумя центральными уровнями, а показатели времени нумеруются нечетными числами:
|

Тогда система нормальных уравнений принимает вид:
- для прямой
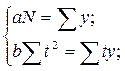
- для параболы второго порядка
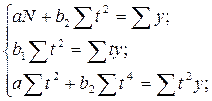
- для экспоненты
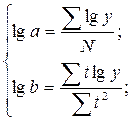
- для гиперболы
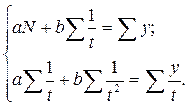
После определения параметров уравнения тренда для ряда динамики рассчитываются теоретические значения уровней (т.е. соответствующие функции тренда) и анализируются их отклонения от фактических уровней ряда динамики, характеризующие ошибки тренда. Как и в классических регрессионных моделях, описанных с помощью МНК, в качестве меры точности найденной функции используют коэффициент детерминации:
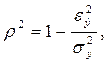
где 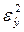 - остаточная дисперсия;
- остаточная дисперсия;
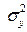 - общая дисперсия.
- общая дисперсия.
Данные табл. 5.6 и их графическое изображение (рис. 5.1.) позволяют предположить наличие линейной или параболической основной тенденции. Для нахождения аналитического выражения тренда перейдем к новой временной шкале. Необходимые данные для расчета параметров линейного и параболического (второго порядка) трендов приведены в табл. 5.7.
Таблица 5.7
Динамика объема продаж условного товара и определение параметров уравнения тренда МНК
| Год | Объем продаж, млн. шт./год | t | t2 | yt | t4 | yt2 | y2 |
| -7 | -7 | ||||||
| -6 | -18 | ||||||
| -5 | -25 | ||||||
| -4 | -8 | ||||||
| -3 | -27 | ||||||
| -2 | -14 | ||||||
| -1 | -5 | ||||||
| Итого |
Тогда система нормальных уравнений принимает вид:
- для прямой
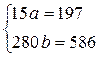
- для параболы второго порядка
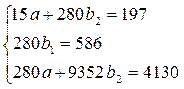
Решая системы, получаем следующие уравнения тренда:
- для прямой
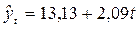
- для параболы второго порядка
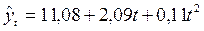 .
.
Графическое изображение полученных линий тренда представлено на рис. 5.2.
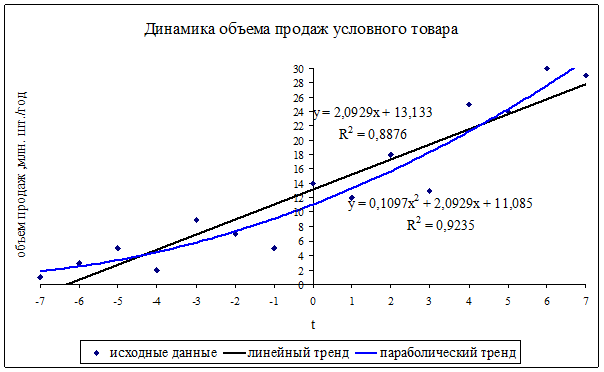
Рис. 5.2. Динамика объема продаж условного товара. Аналитическое выравнивание.
Для оценки найденных уравнений тренда в табл. 5.8 рассчитаны значений объема продаж по каждому регрессионному уравнению и ошибки трендов.
Используя данные об ошибках регрессионных значений, рассчитаем коэффициенты детерминации:
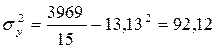
- для прямой
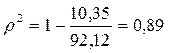
- для параболы второго порядка
 .
.
Оба уравнения тренда достаточно хорошо описывают основную тенденцию динамики объема продаж.
Таблица 5.8
Регрессионные значения объема продаж
| t | Объем продаж, млн. шт./год | Линейный тренд
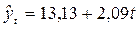
| Параболический тренд
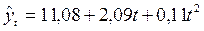
| ||
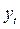
| 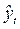
| 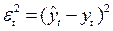
| 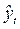
| 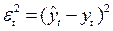
| |
| -7 | -1,52 | 6,33 | 1,81 | 0,66 | |
| -6 | 0,58 | 5,87 | 2,48 | 0,27 | |
| -5 | 2,67 | 5,43 | 3,36 | 2,68 | |
| -4 | 4,76 | 7,63 | 4,47 | 6,10 | |
| -3 | 6,85 | 4,60 | 5,79 | 10,28 | |
| -2 | 8,95 | 3,79 | 7,34 | 0,11 | |
| -1 | 11,04 | 36,49 | 9,10 | 16,83 | |
| 13,13 | 0,75 | 11,09 | 8,50 | ||
| 15,23 | 10,41 | 13,29 | 1,66 | ||
| 17,32 | 0,46 | 15,71 | 5,25 | ||
| 19,41 | 41,11 | 18,35 | 28,64 | ||
| 21,50 | 12,22 | 21,21 | 14,35 | ||
| 23,60 | 0,16 | 24,29 | 0,09 | ||
| 25,69 | 18,57 | 27,59 | 5,80 | ||
| 27,78 | 1,48 | 31,11 | 4,46 | ||
| Итого | 197,00 | 155,32 | 197,00 | 105,65 | |
| В среднем | 13,13 | 13,13 | 10,35 | 13,13 | 7,04 |
После описания основной тенденции ряда динамики она исключается путем последовательного вычитания из фактических уровней их выровненных значений (для аддитивной модели) или путем деления фактических уровней на теоретические (для мультипликативной модели). Таким образом, в результате исключения тренда, образуется стационарный ряд динамики, или ряд остатков первого рода, для которого можно поставить задачу выявления и описания сезонных колебаний.
Методы выявления сезонных колебаний в рядах динамики
Сезонные колебания обычно связаны со сменой времен года и повторяются регулярно с интервалом в один год. Поэтому для выявления устойчивой сезонной волны необходим анализ распределенных по месяцам (кварталам, декадам) данных за несколько лет (не менее трех).
Для оценки сезонных колебаний (сезонных волн) могут быть использованы следующие методы: абсолютных или относительных разностей, построения индексов сезонности, аналитического выравнивания.
Метод расчета индексов сезонности основан на построении аналитической группировки. Для этого остатки первого рода группируются по периодам/моментам времени внутри года (по месяцам, кварталам, декадам). Затем для каждого периода/момента вычисляется среднее значение стационарного ряда за имеющееся число лет. Набор этих значений можно рассматривать как индексы сезонности, которые описывают сезонную волну.
Если стационарный ряд получен по аддитивной модели, сумма всех индексов сезонности должна равняться нулю; если по мультипликативной – числу сезонов.
Метод аналитического выравниваниязаключается в подборе функции для описания сезонной волны. Это может быть сделано на основе гармонического анализа, при котором периодическая функция описывается с помощью гармонического ряда Фурье. С помощью данного подхода динамический процесс представляется в виде функции времени, в которой слагаемые расположены по убыванию периодов. Первая гармоника ряда Фурье имеет вид:
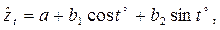
где  - выровненные уровни стационарного ряда;
- выровненные уровни стационарного ряда;
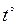 - показатель времени, имеющий градусную меру.
- показатель времени, имеющий градусную меру.
Параметры уравнения определяются методом наименьших квадратов. Если данная функция применяется к стационарному ряду, то параметр 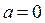 . Так как функция периодическая, время в этой модели имеет градусную меру.
. Так как функция периодическая, время в этой модели имеет градусную меру.
В табл. 5.9 представлены исходные и расчетные данные для описания сезонной волны. По условным данным о динамике расхода электроэнергии была описана основная тенденция в виде линейной функции  , определены остатки первого рода,
, определены остатки первого рода, 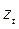 , для которых и поставлена задача выявления и описания сезонной волны.
, для которых и поставлена задача выявления и описания сезонной волны.
Таблица 5.9
Динамика ежеквартального расхода электроэнергии в 2003-2005 гг. (условные данные)
| Год | Квартал | Расход э/энергии, тыс. кВт-час
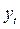
| t | 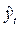
| 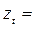

| 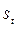
| 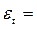
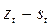
|
| I | -11 | 315,77 | 24,23 | 22,67 | 1,56 | ||
| II | -9 | 321,99 | -11,99 | -20,22 | 8,23 | ||
| III | -7 | 328,22 | -78,22 | -79,78 | 1,56 | ||
| IV | -5 | 334,44 | 85,56 | 77,33 | 8,23 | ||
| I | -3 | 340,66 | 19,34 | 22,67 | -3,33 | ||
| II | -1 | 346,89 | -16,89 | -20,22 | 3,33 | ||
| III | 353,11 | -73,11 | -79,78 | 6,67 | |||
| IV | 359,34 |
|
Главная страница Случайная страница Контакты