
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ИНДЕКСЫ. Цель: познакомить студентов с важнейшими приемами индексного анализа связи и изменения признаков с разнородными элементами
Цель: познакомить студентов с важнейшими приемами индексного анализа связи и изменения признаков с разнородными элементами, а также показателей совокупности однородных единиц.
Задачи: характеристика условий формирования системы индексов, методики построения агрегатной формы индексов и средних из индивидуальных, индексов средних величин и территориальных индексов.
Виды индексов. Правила построения индексов
Понятие индекс имеет латинский корень index показывающий, указатель. Распространенное однокоренное слово – индикатор.
В статистике под индексом понимается относительный показатель, характеризующий результат сравнения двух уровней объекта. Можно выделить результаты изменения величины во времени (динамические индексы), в пространстве (территориальные индексы), по отраслям (отраслевые индексы) и другие.
Величина, изменение которой измеряется с помощью индекса, называется индексируемой величиной. Так в индексе цен индексируемой величиной является цена, в индексе физического объема индексируемой величиной является физический объем (объем выпуска в натуральном выражении).
Данные текущего уровня (величина, которая сравнивается) принято обозначать значком «1» (x1 или x1), а данные базисного уровня, служащего базой сравнения, обозначаются со значком «0» (x0 или x0).
Индекс строится как отношение индексируемой величины на текущем уровне к значению индексируемой величины на базисном уровне.
По степени охвата элементов явления (представляющих собой единицы совокупности) индексы разделяют на индивидуальные и сводные (общие).
Индивидуальный индексизмеряет изменение отдельного элемента явления (например, изменение объема выпуска телевизоров определенной марки, рост или падение цен на акции в некотором акционерном обществе и т.д.). Индивидуальные индексы обозначаются «i» и снабжаются подстрочным знаком индексируемого показателя: iq - индивидуальный индекс физического объема определенного вида продукции, ip – индивидуальный индекс цен на определенный вид продукции и т.д.
Индивидуальные индексы относятся к одному элементу и рассчитываются как отношение двух индексируемых величин:
 .
.
Например, ip = p1/p0 - индивидуальный индекс цен, где p1,p0 - цены единицы продукции в текущем (отчетном) и базисном периодах. iq = q1/q0 - индивидуальный индекс физического объема продукции.
Сводный (общий) индекс характеризует изменение всех элементов явления. Например, изменение физического объема продукции предприятия, выпускающего разноименные товары; изменение цены на разные группы товаров и т.д.
Если индексы охватывают не все элементы явления, а лишь часть, то их называют групповыми или субиндексами (например, индексы продукции по отдельным отраслям промышленности).
Сводный индекс обозначается буквой «I» и также сопровождается подстрочным знаком индексируемого показателя: например, Ip - сводный индекс цен; Iz - сводный индекс себестоимости.
Сводные (общие) индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных индексов.
Агрегатные индексы - основная форма индексов
Основной формой индексов являются агрегатные индексы.
«Агрегатным» он называется потому, что его числитель и знаменатель представляют собой набор – «агрегат» (от латинского aggregatus – складываемый, суммируемый) элементов, относящихся к изучаемому явлению. Агрегатный индекс строится как отношение сумм произведений двух величин: 1) индексируемой величины - х, которая меняется в числителе по сравнению со знаменателем, 2) соизмерителя (веса индекса) - f, который остается неизменным в числителе и знаменателе. Произведение индексируемой величины на вес индекса (соизмеритель) называют результативным показателем.
 ( I = ∑x1f /∑x0f)
( I = ∑x1f /∑x0f)
где х1 – сравниваемое (текущее) значение данного признака;
х0 – базисное значение, относящееся к базовому периоду времени, либо базовому объекту сравнения;
j – номер элемента, совокупность которых образует сложное явление (j = 1; J);
хj·fj – результативный показатель для i–ого элемента.
Важной особенностью агрегатных индексов является то, что они обладают синтетическими и аналитическими свойствами. Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение в целое разнородных единиц статистической совокупности. Аналитические свойства определяются тем, что с помощью индексного метода можно оценить влияние факторов на изменение изучаемого показателя.
Важным моментом при построении агрегатных индексов является выбор системы весовых коэффициентов: это могут быть значения на базисном или текущем уровне, плановые значения, нормативные или условные значения. В каждом случае веса должны быть обоснованы и должны соответствовать цели, для которой используется индекс и реальным экономическим условиям.
Если в качестве весов брать значения признака-веса за базисный период времени (или относящиеся к базисному объекту), то формула агрегатного индекса примет вид:

Ее еще называют агрегатной формой индекса Ласпейреса (по имени ученого Э. Ласпейреса, предложившего ее впервые в 1864 г.).
Если в качестве весов брать значения признака-веса за текущий период времени (или относящиеся к текущему объекту), то формула агрегатного индекса примет вид:

Ее еще называют агрегатной формой индекса Пааше (по имени ученого Г.Пааше, предложившего ее впервые в в 1874 г.).
Можно построить общий индекс как среднее геометрическое из индексов Ласпейреса и Пааше:
 .
.
Этот способ предложил Фишер и назвал данную формулу «идеальным индексом».
Различают индексы объемных (количественных) и качественных показателей.
Объемные индексы служат для измерения изменения объемных показателей. Объемные показатели выражаются абсолютными величинами. Например, объем выпуска продукции, численность работающих.
Качественные индексы служат для измерения изменения качественных показателей. Качественный показатель определяется в расчете на количественную единицу. Примером таких показателей могут служить: цена, себестоимость единицы продукции, трудоемкость единицы продукции, производительность труда и т.п.
В качестве веса индекса при построении индекса объемного показателя выступает качественный показатель. Рассмотрим построение агрегатного индекса на примере индекса физического объема.
В данном случае индексируемой величиной будет q – показатель физического объема выпуска продукции в натуральных единицах измерения. Весом индексирования может быть цена – p.
Весом индексирования при построении индекса качественного показателя выступает объемный показатель. Рассмотрим построение агрегатного индекса на примере качественного показателя – p цены за единицу продукции. Весом индекса будет физический объем выпуска (q). Результативный показателем при этом будет общая стоимость произведенной продукции (p·q).
В экономике часто встречаются показатели, определяемые как произведение двух сомножителей, один из которых показатель качественный, другой объемный. Это две стороны одного явления, однако они по разному влияют на результат. Качественный (интенсивный) фактор относится ко всей совокупности. Является средней характеристикой всей объемной величины. Нас интересует результат его влияния в текущем периоде, при фактическом (текущем) объеме и изменение качественного показателя оценивается на фоне текущего значения объемной величины.
Изменение объемного (экстенсивного) показателя оценивается на фоне базисного уровня качественного фактора.
Такой порядок исчисления индексов и определения степени влияния факторов на результат относится ко всем случаям взаимосвязанных показателей, когда результирующий показатель есть произведение двух факторов, один из которых качественный, другой - объемный. Например, общие затраты на производство в денежных единицах - z∙q (z-себестоимость единицы продукции, q – показатель физического объема выпуска продукции в натуральных единицах измерения), затраты времени на производство данного объема продукции – t∙q (t-трудоемкость единицы продукции).
Рассмотрим построение индексов для случая взаимосвязанных показателей для стоимости продукции S, цены за единицу продукции p и физического объема продукции q.
Индивидуальные индексы показателей имеют вид:
- физического объема работ или услуг
iq = q1/q0,
- цены
ip =p1/p0,
- стоимости
ipq =p1q1/p0q0 или is =p1q1/p0q0
Агрегатный индекс физического объема работ или услуг (индекс объемного показателя) строится как индекс Ласпейреса по базисным ценам (p0):

Агрегатный индекс цен (индекс качественного показателя) строится как индекс Пааше по текущим значениям физического объема (q1):

Сводный индекс результативного показателя представляет собой отношение суммы результативных показателей текущего периода (объекта) к сумме результативных показателей базисного периода (объекта):
 .
.
Например, отношение стоимости продукции отчетного (текущего) периода S1=q1·p1 к стоимости продукции базисного периода S0=q0·p0 представляет собой сводный индекс стоимости продукции или товарооборота:
 или Is = ∑ q1·p1/∑ q0·p0.
или Is = ∑ q1·p1/∑ q0·p0.
Этот индекс показывает во сколько раз в среднем возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным.
Рассмотрим пример. Имеются данные о фактическом выпуске и ценах на продукцию машиностроительным предприятием за два года (табл. 6.1). Необходимо рассчитать сводные и индивидуальные индексы.
Таблица 6.1
Данные о фактическом выпуске и ценах на продукцию машиностроительного предприятия
| Виды продукции | Выпуск продукции в натуральном выражении | Цена производителя за единицу, млн.руб. | Индивидуальные индексы физического объема продукции: iq=q1/q0 | Индивидуальные индексы цен: ip=p1/p0 | Индивидуальный индекс стоимости: ipq=p1·q1/p0·q0 | ||
| Базисный период q0 | Отчетный период q1 | Базисный период p0 | Отчетный период p1 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1,5 | 1,1(6) | 1,75 | |||||
| 1,4 | 0,875 | 1,225 | |||||
| 1,(3) | 1,(3) |
Расчет индивидуальных индексов приведен в таблице (столбцы 6, 7, 8).
Общий индекс физического объема:
 .
.
В целом по трем видам продукции наблюдается рост физического объема выпуска за рассматриваемый период на 39%.
Общие индексы цены:
 .
.
В целом по трем видам продукции наблюдается снижение цен за рассматриваемый период на 3,5%.
Общие индексы стоимости:
 .
.
В целом по трем видам продукции за рассматриваемый период стоимость возросла на 34%.
Средние (арифметические и гармонические) индексы на основе индивидуальных индексов: их связь с агрегатными индексами
Сводный индекс может быть построен как средняя взвешенная величина из индивидуальных индексов. Выбор вида средней (арифметическая или гармоническая) зависит от используемых весовых коэффициентов. При этом значение среднего индекса должно совпадать со значением агрегатного индекса (Ласпейреса или Пааше). Весами усреднения выступают в данном случае результативные показатели (либо базисного, либо текущего уровня): fj=xj·fj.
 ;
;  .
.
Вид степенной средней зависит от имеющейся в нашем распоряжении информации.
Если имеются данные об индивидуальных индексах ixj и о значении результативного показателя за базисный период времени (либо относящиеся к базисному объекту) f0j = x0j · f0j, то усреднение происходит по формуле средней арифметической взвешенной с весами равными результативному показателю базисного периода. Данный индекс тождественен агрегатной форме индекса Ласпейреса:

Если имеются данные об индивидуальных индексах ixj и о значении результативного показателя за текущий период времени (либо относящиеся к текущему объекту) f1j = x1j · f1j, то усреднение происходит по формуле средней гармонической взвешенной с весами равными результативному показателю текущего периода. Данный индекс тождественен агрегатной форме индекса Пааше:

В качестве весов могут приниматься не только абсолютные значения результативного показателя, но и относительные величины - доли, проценты результативного показателя отдельной единицы (элемента) в общем объеме результативного показателя по совокупности (явлению) в целом:
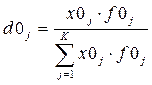 ,
,  ;
;
 ,
,  .
.
Если строятся сводные индексы качественных показателей, то используется формула среднего гармонического взвешенного по текущим значениям результата. Так сводный индекс цен определяется как среднее гармоническое из индивидуальных индексов цен (ip), взвешенное по текущей (фактической) стоимости (p1q1):

При построении сводных индексов объемных показателей используется формула среднего арифметического взвешенного по базисным значениям результата. Сводный индекс физического объема продукции рассчитывается как среднее арифметическое из индивидуальных индексов (iq), взвешенное по базисной стоимости (p0q0):
 .
.
По данным нашего примера (таблицы) рассчитаем сводные индексы физического объема и цены как средние из индивидуальных.
Сводный индекс физического объема продукции:
 .
.
Сводный индекс цен:

Значения индексов, рассчитанных как агрегатные и как средние из индивидуальных, совпали.
Индексный метод используется для определения влияния различных факторов на изменение результата как в относительном, так и в абсолютном выражении.
Некоторые экономические показатели находятся между собой в определенной (функциональной) связи, например, в виде произведения (либо отношения). В таком же соотношении должны находиться и статистические показатели, характеризующие изменение исходных экономических показателей, т.е. индексы: если z = x · y , то Iz = Ix · Iy
Для индивидуальных индексов это очевидно:

При построении сводного индекса соотношение Iz=Ix·Iy осуществимо, если веса индексирования для Ix и Iy берутся за разные периоды времени (или относятся к разным объектам), т.е. один из индексов должен быть построен по формуле Ласпейреса, а другой - по формуле Пааше:
 .
.
Если один из сомножителей показатель качественный, а другой - объемный, то, как уже было отмечено, индекс качественного показателя определяется по текущим значениям объемного показателя.
Общая стоимость продукции равна произведению цены за единицу продукции на физический объем выпуска: ∑S = ∑p·q. Тогда сводный индекс стоимости должен быть равен произведению сводного индекса цен на сводный индекс физического объема Is = Ip·Iq. Чтобы выполнялось данное условие необходимо, чтобы веса при построении индексов цен и физического объема относились к разным уровням. Принято вычислять индекс цен по формуле Пааше, а индекс физического объема по формуле Ласпейреса:
 .
.
При этом Is показывает общее изменение стоимости, индекс цены Ip – как изменилась стоимость за счет изменения цен, а Iq – как изменилась стоимость за счет изменения физического объема продукции.
В нашем примере (табл. 6.1) общий индекс стоимости:




Таким образом, стоимость продукции выросла на 34 %, в том числе за счет увеличения объема выпуска продукции на 39 %, а в связи со снижением цен снизилась на 3,5 %.
Индексный метод анализа влияния факторов
Индексный метод позволяет также представить абсолютное изменение результативного показателя(Dz), как результат влияния различных факторов (входящих в формулу его расчета).
Общее абсолютное изменение результативного показателя текущего уровня по сравнению с базисным определяется как разница между числителем и знаменателем в формуле соответствующего аналитического сводного индекса данного результативного показателя.
Абсолютный прирост стоимости продукции может быть представлен как:
 .
.
И разложен на:
1. абсолютный прирост стоимости за счет изменения цен:
 .
.
2. абсолютный прирост стоимости за счет изменения количества выпускаемой продукции:
 .
.
Общее абсолютное изменение стоимости продукции равно алгебраической сумме изменений за счет каждого из факторов:
Ds = Dsp + Dsq .
По данным рассмотренного примера стоимость продукции составила в базисном периоде s0 = ∑p0q0 = 8200 тыс.руб., в текущем периоде s1 = ∑p1q1 =11000 тыс.руб., стоимость продукции текущего периода по базисным ценам ∑p0q1 = 11400 тыс.руб.
Общее изменение стоимости продукции Ds = s1 - s0 = 11000 – 8200 = 2800 тыс.руб.
В том числе за счет:
- изменения цен Dsp = ∑p1q1 - ∑p0q1 = 11000 – 11400 = -400 тыс. руб. стоимость продукции уменьшилась на 400 тыс.руб.
- за счет изменения объема выпуска продукции Dsq = ∑p0q1 - ∑p0q0 = 11400–8200=3200 тыс.руб. стоимость продукции выросла на 3200 тыс.руб.
Пусть по предприятию имеются данные о выпуске продукции Q и численности работающих T за два периода времени. В базисном периоде выпуск продукции составил 20000 тыс.руб., число работающих – 200 чел., в текущем периоде выпуск продукции составил 23100 тыс.руб., число работающих – 220 чел. Необходимо проанализировать изменение выпуска продукции.
Уровень производительности труда (выработка на одного работающего) в базисном периоде W0 = Q0/T0 = 100 тыс.руб./чел., в текущем периоде W1 = Q1/T1= 23100/220 = 105 тыс.руб./чел.
По каждому показателю рассчитаем индексы и абсолютные приросты, данные сведены в табл. 6.2.
Таблица 6.2
Анализ влияния факторов на изменение объема выпуска
| Базисный период | Текущий период | Абсолютный прирост (∆) | Индекс (i) | |
| Q | +3100 | 1,155 | ||
| T | +20 | 1,1 | ||
| W | +5 | 1,05 |
IQ = 1,1 · 1,05 = 1,155 = 115,5 %.
Таким образом, объем продукции увеличился на 15,5 %, в том числе:
- за счет роста затрат труда на 10 % - экстенсивный фактор;
- за счет роста производительности труда на 5 % - интенсивный фактор.
Общее изменение выпуска продукции в абсолютном выражении:

В том числе за счет увеличения затрат труда (экстенсивный фактор оценивается по базисному значению качественного фактора W0):

За счет повышения производительности труда (качественный, интенсивный фактор оценивается по текущему значению объемного фактора T1):

Общее изменение: 2000 + 1100 = 3100 .
Индексы постоянного и переменного состава. Индекс среднего уровня и учет в нем изменения структуры; индекс структурного сдвига
Индексный метод используется и в анализе средних величин. В отличие от агрегатных данные индексы рассчитываются по качественно однородным совокупностям, состоящим из сопоставимых элементов.
Индекс средней цены (качественного признака):
 .
.
Если принять  - удельный вес количества группы в общем количестве, получим:
- удельный вес количества группы в общем количестве, получим:

На величину индекса средней цены влияет как изменение цен, так и изменения структуры набора продукции, для которой определялась средняя цена, поскольку в ее расчете участвуют веса разных периодов (q0 и q1) и (u0 и u1). Поэтому индекс средней величины называется индексом переменного состава. Индекс переменного состава показывает, как изменилось среднее значение признака.
Для анализа влияния непосредственного изменения цен рассчитывают индекс постоянного (фиксированного) состава:

 .
.
Индекс постоянного состава показывает как изменилось среднее значение признака за счет изменения самого признака, то есть изменение средней цены на продукцию за счет изменения цен.
Для определения влияния изменения структуры продукции рассчитывается индекс структурного сдвига:
 .
.
Индекс структурного сдвига показывает как изменилось среднее значение признака в связи с изменением структуры, то есть изменение средней цены на продукцию за счет изменения удельных весов в общем объеме продукции групп с разным уровнем цены за единицу продукции.
Индексы переменного состава, постоянного состава и структурного сдвига связаны между собой:

Данный метод применим для оценки влияния структурных сдвигов на изменение средних значений качественных показателей (производительности труда, среднего заработка, себестоимости единицы продукции и других).
Таблица 6.3
Анализ изменения средней себестоимости
| Пред- приятие | Выпуск продукции, тыс. единиц | Себестоимость единицы продукции, тыс. руб. | Доля предприятия в общем выпуске | |||
| базисный q0 | текущий q1 | базисная z0 | текущая z1 | базисная u0 | текущая u1 | |
| №1 | 0,25 | 0,80 | ||||
| №2 | 0,75 | 0,20 | ||||
| Сумма | х | х | 1,00 | 1,00 |
Пусть, однородная продукция выпускается на двух предприятиях отрасли. Данные по предприятию приведены в табл. 6.3.
Индекс средней себестоимости (индекс переменного состава):
 .
.
Средняя себестоимость выросла в 1,73 раза или на 72,8 %.
 .
.
За счет роста себестоимости на предприятиях средняя себестоимость единицы продукции выросла в 1,2 раза или на 20%., или себестоимость единицы продукции увеличилась в среднем на 20%.
Индекс структурного сдвига:
 или
или 
За счет изменения структуры выпуска продукции средняя себестоимость выросла на 44%. Увеличилась доля выпуска продукции с 0,25 до 0,8 на предприятии №1 с более «дорогой» продукцией, что и повысило среднюю себестоимость на 44%.
Особенности построения индексов экономических показателей
В разделах экономической статистики рассматриваются индексы конкретных экономических показателей. Однако, нужно сделать несколько замечаний.
Одним из важнейших показателей статистики цен является индекс потребительских цен (ИПЦ). При расчете ИПЦ производится отбор товаров (услуг), по которым производится регистрация цен. Он производится в соответствии с общероссийским классификатором экономической деятельности, продукции и т.д. Затем формируется структура весов по отдельным группам товаров и услуг для расчета сводного индекса потребительских цен. Для этого используются данные о структуре потребительских расходов населения.
Пересчет важнейших стоимостных показателей системы национальных счетов из фактических цен в сопоставимые осуществляется с помощью индекса – дефлятора. Дефлятор – это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного.
Для расчета индекса Пааше требуется взвешивание по весам отчетного периода, что в масштабах страны требует очень больших затрат. Начиная с 1991 года индекс цен в России определяется как индекс Леспейреса. При этом весовые коэффициенты по выпуску продукции фиксируются на уровне базисного периода и остаются неизменными в течение некоторого промежутка времени. Целью расчета индекса является измерение динамики стоимости базисного (неизменного) объема продукции. Чем дальше от базисного периода, тем менее надежен расчетный индекс цен. Система весов должна вовремя пересматриваться.
Контрольные вопросы
1. Что представляет собой индекс? Как он интерпретируется с точки зрения синтетической и аналитической теорий индексов?
2. Какие виды индексов принято выделять в статистике?
3. Как строится агрегатный индекс?
4. Как построить сводный индекс на основе индивидуальных?
5. Опишите индексный метод анализа факторов в изменении сложного явления.
6. Как с помощью индексов проанализировать изменение средней величины?
7. Что представляют собой ряды индексов?
8. Назовите виды рядов индексов.
Дата добавления: 2014-12-23; просмотров: 869; Мы поможем в написании вашей работы!; Нарушение авторских прав |