МОДУЛЬ 2. ТЕОРИЯ КРИТИЧЕСКИХ РАЗМЕРОВ

Рис.11.5. Блок - схема универсального алгоритма чтения односторонней таблицы решений.

Возможная структура массивов информации, построенных на основе односторонней таблицы решений и заполненных данными рассматриваемого примера, приведена на рис. 11.6. Пусть , т.е. В соответствии с алгоритмом поиск решения в этом случае будет осуществляться:

Т.е. решением в данном случае будет станок модели 5А702Г.

Лекция 11 Стр. 5 из 6

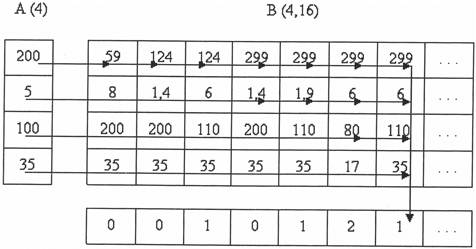
С(16)

Рис.11.6. Структура массивов информации, построенных на основе односторонней таблицы решений (фрагмент)

Двухсторонние таблицы (матрицы) решений

Преобразуем одностороннюю таблицу решений для выбора

зубошевинговального станка в двухстороннюю таблицу - см. табл. 11.5

Таблица 11.5. Фрагмент минимизированной двухсторонней таблицы решений для выбора модели зубошевинговального станка

		,мм при
§	1,4		1,4	1.9		. . .
		-	-	-	-	-		. . .
	-	-	-	-	-	-	. . .
		-	-	-	-	-	-	. . .
	-	-		-			. . .
		-	-	-	-	-	-	. . .
	-	-	-	-	-	-	. . .
Фрагмент	формализованной двухсторонней таблицы (матрицы решений)
		,мм при
59						...
§	1.4		1.4	1,9		. . .
								. . .
								. . .
								. . .

Примечание: при упрощении таблицы не исключена последняя ее строка, т.к. в полной таблице (не во фрагменте) она содержит «ненулевые» клетки.

На рис. 11.7 показана возможная структура массивов информации, построенных на основе двухсторонней таблицы решений и заполненных данными рассматриваемого примера.

А2(2) В2 (2,15)

А1(2)									299
						1,4		1,4	1,9	-А
110	г	35	г						-^

В1 (2.3) С (3.15)

Лекция 11 Стр. 6 из 6

Рис.11.7. Структура массивов информации, построенных на основе двухсторонней таблицы решений (фрагмент)

Примечание: в отличие от рис. 11.6 на рис. 11.7 показана упрощенная схема поиска решения.

Для поиска решений представленный в виде блок - схемы на рис. 11.5 алгоритм здесь используется дважды: первый раз для нахождения нужной строки, второй раз - нужного столбца (или наоборот) в массиве «С». Как и при использовании односторонней таблицы искомым решением для рассматриваемого примера будет станок модели 5А702Г.

МОДУЛЬ 2. ТЕОРИЯ КРИТИЧЕСКИХ РАЗМЕРОВ

Гомогенный реактор без отражателя в односкоростном приближении. Волновое уравнение реактора. Граничные условия. Материальный и геометрический параметры. Одногрупповое приближение. Геометрический параметр и распределение потока нейтронов по объему реактора. Квазикритическое приближение. Гомогенный реактор без отражателя в диффузионно-возрастном приближении. Уравнение реактора и его решение. Материальный параметр и условие критичности в диффузионно-возрастном приближении. Условие критичности для гомогенного реактора в одногрупповом приближении. Условия применимости. Геометрический параметр для реакторов разной формы. Критический объем и вероятность избежать утечки для разной геометрии. Условие некритического реактора. Временная зависимость плотности потока нейтронов в реакторе при различных соотношениях между материальным и геометрическим параметрами. Коэффициенты неравномерности нейтронного поля (поля энерговыделения). Гомогенный реактор с отражателем в одногрупповом приближении. Влияние отражателя на распределение потока нейтронов в реакторе. Диффузионные уравнения для активной зоны и отражателя. Граничные условия. Условие критичности для плоского реактора с отражателем. Эффективная добавка отражателя. Условие критичности для сферического и бесконечного цилиндрического реактора с отражателем. Геометрический параметр для реакторов с отражателем. Решения волнового уравнения для различных геометрий. Распределение потока нейтронов в активной зоне и отражателе. Метод многих групп. Распределение плотности потока тепловых нейтронов в активной зоне гомогенного реактора без и с отражателем. Энергетические спектры нейтронов в реакторе. Многогрупповое нестационарное уравнение баланса нейтронов. Групповые константы. Гомогенный реактор в двухгрупповом приближении. Система диффузионных уравнений для активной зоны и отражателя. Граничные условия. Волновые уравнения для активной зоны и отражателя. Связь между потоками быстрых и тепловых нейтронов в активной зоне и отражателе. Критическое условие для реактора с отражателем в двухгрупповом приближении. Распределение потоков быстрых и тепловых нейтронов в реакторе с отражателем. Физическое профилирование активной зоны. Многозонный реактор. Условие критичности двухзонного реактора с отражателем в одногрупповом приближении.

Вопросы на итоговую аттестацию по модулю 2:

1. Коэффициенты формулы четырех сомножителей для гомо- и гетерогенного ядерного реактора. Расчет гомогенизированных ядерных концентраций в ячейке (гомогенизация ячейки). Критерий гомогенности (гетерогенности). Фактор проигрыша.

2. Коэффициент использования тепловых нейтронов для гомо- и гетерогенного ЯР. Фактор проигрыша. Вероятность избежать резонансного захвата на уране-238 для гомо- и гетерогенного ЯР. Эффективный и истинный резонансный интеграл поглощения. Фактор самоэкранирования. Зависимости j и q от диаметра топливной таблетки (типа реактора – гомо-гетеро).

3. Физические особенности гетерогенных ядерных реакторов. Влияние соотношения «замедлитель-топливо» (водо-уранового) соотношения на внешний и внутренний блок-эффекты и на эффективный коэффициент размножения нейтронов в ядерном реакторе. Количественные характеристики блок-эффектов.

4. Общая методика решения диф. уравнения диффузии для активной зоны ядерного реактора. Условие критичности для гомогенного голого ядерного реактора конечных размеров. Материальный и геометрический параметры и их величины, их соотношение в реакторе.

5. Критические размеры гомогенных голых реакторов различной геометрии, их геометрические параметры, распределение плотности потока нейтронов (пластина, сфера, параллелепипед, цилиндр).

6. Критическая масса и критический объем. Минимальный критобъем гомогенного голого реактора различной геометрии. Коэффициенты неравномерности нейтронного потока для гомогенного голого реактора конечных размеров различной геометрии (пластина, сфера, параллелепипед, цилиндр).

7. Функции отражателя. Эквивалентный реактор. Эффективная добавка отражателя. Тонкий и толстый отражатель, бесконечно толстый отражатель.

8. Гомогенный реактор с отражателем в одногрупповом приближении. Методика получения условия критичности.

9. Гомогенный реактор с отражателем в двухгрупповом приближении. Методика получения условия критичности. Распределение тепловых нейтронов в отражателе.

10. Понятие «большого» или «малого» ЯР с точки зрения размеров и величины утечки нейтронов из активной зоны ядерного реактора (качественное объяснение).

11. Коэффициенты неравномерности поля энерговыделения в ядерном реакторе и способы их уменьшения. Физическое профилирование.

12. Метод многих групп. Выбор числа групп. Подготовка групповых констант. Многогрупповое уравнение для плотности потока нейтронов, смысл его слагаемых и методика решения. Нормировка констант на удельную тепловую мощность реактора.

13. Метод многих групп. Функция ценности нейтронов. Многогрупповое уравнение для ценности, смысл его слагаемых и методика решения.

14. Метод многих групп. Выбор числа групп. Особенности подготовки многогрупповых констант. Свертка многогрупповых констант для малогрупповых приближений.

15. Методика получения критуравнения реактора.