Яка з формул для обчислення площі області , обмеженої контуром не є правильною ?

а) ;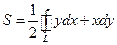

50 Інтеграл не залежить від форми шляху інтегрування, якщо виконана умова:

г) ;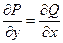

51 Інтеграл не залежить від форми шляху інтегрування, якщо виконані умови:

б) ;

52 Якщо поверхня 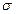задана рівнянням і проектується на площину 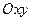в область 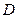, то для обчислення поверхневого інтеграла першого роду має місце формула:

в) ;

53 Якщо поверхня 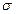задана рівнянням і проектується на площину в область 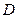, то для обчислення поверхневого інтеграла першого роду має місце формула:

а) ;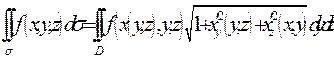

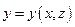54 Якщо поверхня задана рівнянням і проектується на площину в область , то для обчислення поверхневого інтеграла першого роду має місце формула:

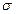б) 55 Площу поверхні можна обчислити за формулою:

б) ;

56 Маса матеріальної поверхні 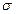, поверхнева густина якої , знаходиться за формулою:

в) ;

57 Координати центра ваги матеріальної поверхні 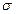, поверхнева густина якої , знаходяться за формулами ( 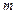- маса поверхні):

в) ;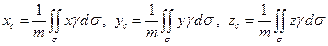

58 Моменти інерції відносно координатних осей матеріальної поверхні 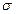, поверхнева густина якої , знаходяться за формулами:

г) ;

59 Момент інерції відносно початку координат матеріальної поверхні 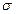, поверхнева густина якої , знаходиться за формулою:

а) ;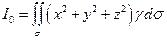

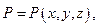
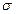60 Зв’язок між поверхневими інтегралами першого і другого роду. Якщо - функції, задані в точках поверхні , - кути між нормаллю до вибраної сторони поверхні 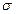та осями відповідно, то має місце рівність:

б)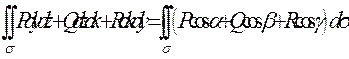

61 Формула Остроградського-Гаусса встановлює зв’язок між:

Дата добавления: 2014-12-30; просмотров: 32; Нарушение авторских прав