Які з наведених нижче рівностей справедливі для криволінійного інтеграла першого роду ?

1) ;

2) ;

3) ;

4) .

Г) 1 і 4

Які з наведених нижче рівностей справедливі для криволінійного інтеграла першого роду ?

2) ;

3) ;

Б) 2 і 3

34 Якщо крива задана рівнянням , то для обчислення криволінійного інтеграла першого роду має місце формула:

а) ;

35 Якщо крива задана рівнянням , то для обчислення криволінійного інтеграла першого роду має місце формула:

в) ;

36 Якщо крива задана параметричними рівняннями , то для обчислення криволінійного інтеграла першого роду має місце формула:

г) ;

37 Якщо просторова крива задана параметричними рівняннями , то для обчислення криволінійного інтеграла першого роду має місце формула:

а) 38 Довжина кривої обчислюється за формулою:

в) ;

39 Маса плоскої матеріальної кривої , лінійна густина якої 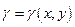, обчислюється за формулою:

б) ;

40 Координати центра ваги плоскої матеріальної кривої , лінійна густина якої 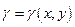, знаходяться за формулами:

б) ;

41 Моменти інерції відносно координатних осей і відносно початку координат плоскої матеріальної кривої , лінійна густина якої 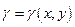, знаходяться за формулами:

в)

Дата добавления: 2014-12-30; просмотров: 25; Нарушение авторских прав