
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тестові теоретичні завдання
Тема: Логика. Основные понятия логики. 2
Тема: Суждения, умозаключения – формы абстрактного мышления. 6
Тема: Алгебра высказываний. 9
Тема: Логические операции. 12
Логическое отрицание. 13
Логическое умножение (конъюнкция). 13
Логическое сложение (дизъюнкция). 14
Операция строгой дизъюнкции. 14
Логическое следование (импликация). 15
Логическое равенство (эквиваленция). 15
Приоритет логических операций. 16
Тема: Построение таблиц истинности сложных высказываний. 18
Тема: Законы алгебры высказываний. 23
Контрольная работа №1. 28
Тема: Логические основы ЭВМ... 29
Логический элемент «НЕ». 30
Логический элемент «И». 30
Логический элемент «ИЛИ». 30
Тема: Решение задач по теме «Логические основы ЭВМ». 33
Контрольная работа №2. 35
Оглавление. 36
Тестові теоретичні завдання
10.2.1. Простір елементарних подій складається з випадкових подій:
а) які є незалежними; б) які є несумісними;
в) які не розкладаються на простіші;
д) інша відповідь.
10.2.2. Сумою двох випадкових подій є подія, яка полягає в тому, що:
а) відбулися обидві події;
б) відбулася тільки одна з двох подій;
в) відбулася хоча б одна з двох подій;
г) не відбулася одна з подій; д) інша відповідь.
10.2.3. Добутком двох випадкових подій є подія, яка полягає в тому, що:
а) відбулися обидві події;
б) відбулася тільки одна з двох подій;
в) відбулася хоча б одна з двох подій;
г) не відбулася одна з подій; д) інша відповідь.
10.2.4. Протилежною до суми двох подій є подія, яка полягає в тому, що:
а) не відбулася хоча б одна із подій;
б) не відбулися обидві події;
г) відбулася хоча б одна із подій; д) інша відповідь.
10.2.5. Протилежною до добутку двох подій є подія, яка полягає в тому, що:
а) відбулася хоча б одна із подій;
в) одна подія відбулася, а інша ні;
г) не відбулася хоча б одна із подій; д) інша відповідь.
10.2.6. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) 1, 2, 3 і 5; б) 1, 2 і 5; в) 2, 3 і 4;
г) 1 і 5; д) інша відповідь.
10.2.7. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3) 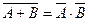 ;
;
4)  ; 5)
; 5)  .
.
а) 1, 2 і 5; б) 2 і 4; в) 2 і 3;
г) 2, 3, 4 і 5; д) інша відповідь.
10.2.8. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 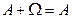 ; 5)
; 5)  .
.
а) 2, 3, 4 і 5; б) всі; в) 1, 3 і 5;
г) 2 і 3; д) інша відповідь.
10.2.9. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 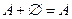 ; 5)
; 5)  .
.
а)1, 2, 3 і 4; б) 3, 4 і 5; в) 1 і 2;
г) 1 і 4; д) інша відповідь.
10.2.10. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 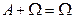 ; 5)
; 5)  .
.
а) 3, 4 і 5; б) 2, 3 і 4; в) 1, 2 , 3 і 4;
г) 3 і 5; д) інша відповідь.
10.2.11. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3) 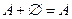 ;
;
4)  ; 5)
; 5)  .
.
а) 1, 3, 4 і 5; б) 2 і 3; в) 3 і 5;
г) 1 і 4; д) інша відповідь.
10.2.12. Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) 1, 2, 3 і 4; б) 1, 3 і 4; в) 2, 3 і 5;
г) 1, 2 і 5; д) інша відповідь.
10.2.13. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулися події
- довільні події. Вкажіть формулу, яка відповідає події: відбулися події  і
і 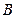 , але не відбулася подія
, але не відбулася подія  .
.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.14. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулася подія
- довільні події. Вкажіть формулу, яка відповідає події: відбулася подія  , а події
, а події 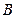 та
та  не відбулися.
не відбулися.
а)  ; б)
; б)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь. 
10.2.15. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулася тільки одна із цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулася тільки одна із цих подій.
а)  ; б)
; б) 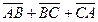 ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.16. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулися рівно дві з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулися рівно дві з цих подій.
а)  ; б)
; б)  ; в)
; в) 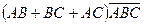 ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.17. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулися всі три з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулися всі три з цих подій.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.18. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: не відбулася жодна з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: не відбулася жодна з цих подій.
а)  ; б)
; б)  ; в)
; в) 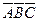 ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.19. Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулася принаймні одна з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулася принаймні одна з цих подій.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.20. Ймовірність суми двох подій  і
і 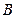 обчислюється за формулою:
обчислюється за формулою:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.21. Ймовірність добутку несумісних подій дорівнює:
а) добутку ймовірностей цих подій;
б) сумі ймовірностей цих подій;
в) нулю; г) одиниці; д) інша відповідь.
10.2.22. Ймовірність добутку незалежних подій дорівнює:
а) відношенню ймовірностей цих подій;
б) сумі ймовірностей цих подій;
в) нулю; г) одиниці; д) інша відповідь.
10.2.23. Протилежна подія має ймовірність, що в сумі з ймовірністю даної події дорівнює:
а) 2; б) 1.5; в) 1; г) 0.5; д) інша відповідь.
10.2.24. Ймовірність події  , що сприяє події
, що сприяє події 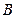 є:
є:
а) меншою за ймовірність 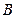 ;
;
б) не більшою за ймовірність 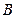 ;
;
в) більшою за ймовірність 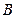 ;
;
г) не меншою за ймовірність 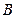 ; д) інша відповідь.
; д) інша відповідь.
10.2.25. Класичне означення ймовірності можна застосувати, коли:
а) простір елементарних подій скінченний; б) завжди;
в) простір елементарних подій складається з рівноможливих елементів;
г) простір елементарних подій містить скінченну кількість рівноможливих елементів;
д) інша відповідь.
10.2.26. Геометричне означення ймовірності можна застосовувати, коли:
а) простір елементарних подій задається множиною евклідового простору;
б) простір елементарних подій задається множиною евклідового простору із скінченною мірою;
в) простір елементарних подій задається множиною евклідового простору із скінченною мірою та всі елементарні події рівноможливі;
г) простір елементарних подій задається множиною евклідового простору та всі елементарні події рівно- можливі;
д) інша відповідь.
10.2.27. Згідно класичного означення ймовірності, ймовірність події дорівнює:
а) відношенню кількості елементарних подій, що сприяють події до кількості всіх рівноможливих елементарних подій;
б) відношенню кількості всіх рівноможливих елементарних подій до кількості елементарних подій, що сприяють події;
в) добутку кількості елементарних подій, що сприяють події та кількості всіх рівноможливих елементарних подій;
г) кількості елементарних подій, що сприяють події;
д) інша відповідь.
10.2.28. Згідно геометричного означення ймовірності, ймовірність події дорівнює:
а) геометричній мірі множини, що задає подію;
б) частці від ділення геометричної міри множини, що задає подію на геометричну міру множини, що задає весь простір елементарних подій;
в) відношенню міри простору елементарних подій до міри події;
г) процентному вмісту події в просторі елементарних подій;
д) інша відповідь.
10.2.29. Згідно теореми множення ймовірностей ймовірність добутку двох подій дорівнює:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
10.2.30. Ймовірність добутку трьох подій обчислюється за формулою:
а)  ;
;
б)  ;
;
в)  ;
;
г) 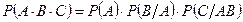 ; д) інша відповідь.
; д) інша відповідь.
10.2.31. Повною групою подій є:
а) набір незалежних рівноймовірних подій;
б) набір несумісних подій, сума яких є достовірною подією;
в) набір незалежних подій, сума яких є достовірною подією;
г) набір подій, сума яких є достовірною подією;
д) інша відповідь.
10.2.32. Група подій називається незалежною в сукупності, якщо:
а) кожні дві події з цієї групи незалежні;
б) ймовірність добутку будь-якого скінченого набору подій з групи дорівнює добутку їх ймовірностей ;
в) ймовірність добутку всіх подій групи дорівнює добутку їх ймовірностей ;
г) ймовірність добутку подій групи дорівнює нулю;
д) інша відповідь.
10.2.33. За формулою повної ймовірності ймовірність події  дорівнює (
дорівнює (  – повна група подій):
– повна група подій):
а)  ; б)
; б) 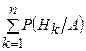 ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.34. Формула Байєса має вигляд (  –повна група подій):
–повна група подій):
а)  ; б)
; б)  ;
;
в) 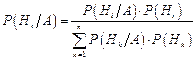 ; г)
; г)  ;
;
д) інша відповідь.
10.2.35. Апостеріорні ймовірності гіпотез можна обчислити за формулою:
а) Байєса; б) Бернуллі; в) Пуассона;
г) повної ймовірності; д) інша відповідь.
10.2.36. Схемою Бернуллі називається схема проведення експериментів:
а) з підкиданням монети; б) з підкиданням грального кубика;
в) незалежних один від одного;
г) однакових і незалежних скінчену кількість раз;
д) інша відповідь.
10.2.37. Ймовірність того, що деяка подія в схемі Бернуллі з  випробувань відбудеться
випробувань відбудеться  раз дорівнює (
раз дорівнює (  – ймовірність цієї події в кожному випробуванні):
– ймовірність цієї події в кожному випробуванні):
а)  ; б)
; б) 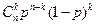 ; в)
; в)  ;
;
г) 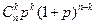 ; д) інша відповідь.
; д) інша відповідь.
10.2.38. Найбільш ймовірною кількістю успіхів в схемі Бернуллі з  випробувань та ймовірністю успіху в кожному з них
випробувань та ймовірністю успіху в кожному з них  є:
є:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 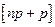 ; д) інша відповідь.
; д) інша відповідь.
10.2.39. При великій кількості випробувань за схемою Бернуллі та малоймовірному успіху в кожному випробуванні ймовірність того, що успіх наступить  раз, може бути наближено обчислена за формулою (
раз, може бути наближено обчислена за формулою (  – кількість випробувань,
– кількість випробувань,  – ймовірність успіху в кожному з них):
– ймовірність успіху в кожному з них):
а)  ; б)
; б)  ; в)
; в) 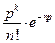 ;
;
г) 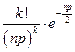 ; д) інша відповідь.
; д) інша відповідь.
10.2.40. Функцією розподілу випадкової величини  є функція:
є функція:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.41. Які з рівностей є правильними ( 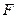 - функція розподілу випадкової величини
- функція розподілу випадкової величини  )?
)?
1)  ; 2)
; 2)  ;
;
3)  ;
;
4) 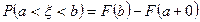 .
.
б) 2 і 4; в) 3 і 4;
г) 2 і 3; д) інша відповідь.
10.2.42. Функція розподілу випадкової величини є:
а) неперервною зростаючою функцією;
;
в) неспадною неперервною зліва функцією;
г) спадною неперервною функцією; д) інша відповідь.
10.2.43. Щільність розподілу випадкової величини - це функція  , для якої (
, для якої ( 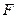 – функція розподілу):
– функція розподілу):
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.44. Основними властивостями щільності розподілу 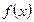 є:
є:
а)  ,
, 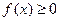 ; б)
; б)  ,
,  ;
;
в)  ,
,  ; г)
; г)  ,
,  ;
;
д) інша відповідь.
10.2.45. Математичним сподіванням дискретної випадкової величини з розподілом  є:
є:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) інша відповідь.
10.2.46. Які з рівностей для математичного сподівання є неправильними (  - випадкові величини,
- випадкові величини,  - постійна)?
- постійна)?
1)  ; 2)
; 2)  ;
;
3)  ;
;
4)  ; 5)
; 5)  .
.
а) тільки 5; б) 3 і 4; в) 3 і 5;
г) 1, 2 і 4; д) інша відповідь.
10.2.47. Чи правильна рівність  ?
?
а) правильна; б) неправильна;
в) правильна, якщо  і
і 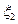 однаково розподілені.;
однаково розподілені.;
г) правильна, якщо  і
і 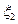 незалежні; д) інша відповідь.
незалежні; д) інша відповідь.
10.2.48. Математичне сподівання неперервної випадкової величини з щільністю розподілу  дорівнює:
дорівнює:
а)  ; б)
; б) 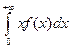 ; в)
; в)  ; г)
; г)  ;
;
д) інша відповідь.
10.2.49. Математичне сподівання випадкової величини задає:
а) її найбільш ймовірне значення; б) її середнє значення;
в) її найменш ймовірне значення;
г) значення, якого потрібно сподіватись;
д) інша відповідь.
10.2.50. Дисперсією випадкової величини  є:
є:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
10.2.51. Дисперсія випадкової величини характеризує:
а) її відхилення від початку координат;
б) її відхилення від середнього значення;
в) квадрат відхилення середнього значення випадкової величини від початку координат;
г) середнє значення різниці випадкової величини та її середнього значення;
д) інша відповідь.
10.2.52. Які з рівностей для дисперсії є неправильними (  - випадкові величини,
- випадкові величини,  - стала)?
- стала)?
1)  ; 2)
; 2) 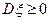 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) 1, 3 і 4; б) тільки 3; в) 3 і 4;
г) 2 і 5;
10.2.53. Середньоквадратичне відхилення випадкової величини є:
а) квадратним коренем з дисперсії цієї величини;
б) середнім значенням квадрата цієї величини;
в) відхиленням середнього значення квадрата випад- кової величини від її середнього значення;
г) квадратом середнього значення цієї величини;
д) інша відповідь.
10.2.54. Випадкова величини  має біноміальний розподіл з параметрами
має біноміальний розподіл з параметрами  і
і  . Які із рівностей є абсолютно правильними?
. Які із рівностей є абсолютно правильними?
1)  , при
, при  ;
;
2)  ; 3)
; 3)  .
.
а) тільки 1; б) тільки 2; в) тільки 3;
г) тільки 1 і 2; д) інша відповідь.
10.2.55. Випадкова величини  має розподіл Пуассона з параметром
має розподіл Пуассона з параметром 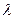 . Які із рівностей є абсолютно правильними?
. Які із рівностей є абсолютно правильними?
1)  , при
, при 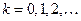 ;
;
2) 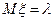 ; 3)
; 3)  .
.
а) тільки 1 і 2; б) тільки 1 і 3; в) тільки 2 і 3;
г) всі; д) інша відповідь.
10.2.56. Випадкова величини  має рівномірний розподіл на відрізку
має рівномірний розподіл на відрізку 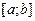 . Які із тверджень є абсолютно правильними?
. Які із тверджень є абсолютно правильними?
1) її щільність розподілу є кусково сталою;
2)  ; 3)
; 3)  .
.
а) всі; б) тільки 1 і 2; в) тільки 1 і 3;
г) тільки 3; д) інша відповідь.
10.2.57. Випадкова величини  має нормальний розподіл з параметрами
має нормальний розподіл з параметрами  і
і  . Які із тверджень є абсолютно правильним?
. Які із тверджень є абсолютно правильним?
1)  ,
,  ; 2)
; 2)  ; 3)
; 3)  .
.
а) тільки 1 і 2; б) тільки 1 і 3; в) тільки 2 і 3;
г) 1, 2 і 3; д) інша відповідь.
10.2.58. Випадкова величина  має нормальний розподіл з параметрами
має нормальний розподіл з параметрами  і
і  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1) щільність розподілу  має вигляд
має вигляд 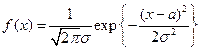 ;
;
2) щільність розподілу  має вигляд
має вигляд  ;
;
3)  ,
, 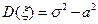 ; 4)
; 4)  ,
,  .
.
а) тільки 1; б) тільки 2 і 4; в) тільки 2 і 3;
г) тільки 1 і 4; д) інша відповідь.
10.2.59. Які із тверджень правильні для функції Лапласа  ?
?
1)  ; 2)
; 2)  ;
;
3) 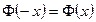 ; 4)
; 4)  ; 5)
; 5)  .
.
а) 3 і 4; б) 1 і 5; в) 2 і 5;
г) 1 і 4; д) інша відповідь.
10.2.60. Функція Лапласа має вид:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
10.2.61. Випадкова величина  має показниковий розподіл з параметром
має показниковий розподіл з параметром 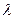 . Які із тверджень є правильними?
. Які із тверджень є правильними?
1) щільність розподілу  має вигляд
має вигляд 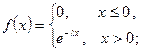
2) щільність розподілу  має вигляд
має вигляд 
3) 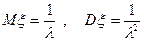 ; 4)
; 4)  .
.
а) 2 і 3; б) 1 і 3; в) 2 і 4;
г) 1 і 4; д) інша відповідь.
10.2.62. Встановити відповідність між щільностями і розподілами.
1)  1) нормальний;
1) нормальний;
2)  2) показниковий;
2) показниковий;
3)  ; 3) рівномірний.
; 3) рівномірний.
а) 1-3, 2-1, 3-2; б) 1-3, 2-2, 3-1; в) 1-1, 2-2, 3-3;
г) 1-2, 2-3, 3-1; д) інша відповідь.
10.2.63. Нехай  – коефіцієнт кореляції випадкових величин
– коефіцієнт кореляції випадкових величин  і
і  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1)  , якщо випадкові величини незалежні;
, якщо випадкові величини незалежні;
2) якщо  , то випадкові величини незалежні;
, то випадкові величини незалежні;
3)  тоді і тільки тоді, коли випадкові величини лінійно залежні.
тоді і тільки тоді, коли випадкові величини лінійно залежні.
а) тільки 3; б) тільки 1 і 3; в) тільки 2 і 3;
г) тільки 1 і 2; д) інша відповідь.
10.2.64. Коефіцієнтом кореляції двох випадкових величин  і
і  є число рівне:
є число рівне:
а)  ; б)
; б)  ;
;
в) 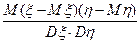 ; г)
; г) 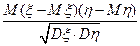 ;
;
д) інша відповідь.
10.2.65. Які із наведених значень є параметрами нормального розподілу на площині (двовимірного нормально розподіленого випадкового вектора)?
1) математичні сподівання кожного з елементів вектора;
2) медіани кожного з елементів вектора;
3) математичне сподівання добутку елементів вектора;
4) коефіцієнт кореляції елементів вектора;
5) коваріація елементів вектора;
6) дисперсії елементів вектора;
7) сума дисперсій елементів вектора.
а) тільки 1, 4 і 7; б) тільки 2, 5 і 4; в) тільки 1, 4 і 6;
г) тільки 2, 4 і 6; д) інша відповідь.
10.2.66. Згідно із законом великих чисел правильними є такі твердження:
1) малоймовірно, що середнє арифметичне відхилень випадкових величин від своїх математичних сподівань значно відрізняється від 0, при великій кількості незалежних випадкових величин.
2) Сума великої кількості випадкових величин має приблизно нульове математичне сподівання та одиничну дисперсію.
3) Відносна частота успіху в схемі Бернуллі мало відрізняється від ймовірності успіху в кожному з випробувань, при великій кількості випробувань.
а) тільки 1; б) тільки 2; в) тільки 3;
г) тільки 1 і 2; д) інша відповідь.
10.2.67. Нехай  – послідовність незалежних однаково розподілених випадкових величин з математичним сподіванням
– послідовність незалежних однаково розподілених випадкових величин з математичним сподіванням  і дисперсією
і дисперсією  . Які з тверджень є правильними?
. Які з тверджень є правильними?
1)  має стандартний нормальний розподіл;
має стандартний нормальний розподіл;
2)  ;
;
3)  при великих
при великих  має приблизно нормальний розподіл з середнім
має приблизно нормальний розподіл з середнім  і дисперсією
і дисперсією  .
.
4) 
а) тільки 1 і 2; б) тільки 2 і 3; в) тільки 3 і 4;
г) тільки 2, 3 і 4; д) інша відповідь.
10.2.68. Нехай 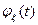 – характеристична функція випадкової величини
– характеристична функція випадкової величини  . В яких із тверджень допущені помилки?
. В яких із тверджень допущені помилки?
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  .
.
а) тільки в 1 і 2; б) тільки в 2 і 3; в) тільки в 3 і 4;
г) тільки в 1 і 4; д) інша відповідь.
10.2.69. Впорядкуйте шкали вимірювань від найпростішої до найбільш багатої.
1) шкала найменувань; 2) шкала порядку;
3) шкала відношень; 4) шкала інтервалів.
а) 1, 2, 3, 4; б) 2, 1, 4, 3; в) 2, 1, 3, 4;
г) 1, 2, 4, 3; д) інша відповідь.
10.2.70. Точкова оцінка  параметра
параметра  розподілу генеральної сукупності називається незміщеною, слушною (консистентною) та ефективною, якщо виконуються такі з наведених вимог:
розподілу генеральної сукупності називається незміщеною, слушною (консистентною) та ефективною, якщо виконуються такі з наведених вимог:
1) 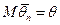 ; 2)
; 2)  , при
, при  ;
;
3)  , при
, при  для всіх
для всіх  ;
;
4)  ;
;
5)  є мінімальною серед дисперсій інших оцінок параметра
є мінімальною серед дисперсій інших оцінок параметра  ;
;
6)  є мінімальною серед дисперсій інших незміщених оцінок параметра
є мінімальною серед дисперсій інших незміщених оцінок параметра  .
.
а) 1, 2 і 3 відповідно; б) 1, 3 і 6 відповідно;
в) 2, 4 і 6 відповідно; г) 2, 4 і 5 відповідно;
д) інша відповідь.
10.2.71. Які з оцінок є оцінками математичного сподівання?
1)  ; 2) медіана; 3)
; 2) медіана; 3)  ; 4) мода.
; 4) мода.
а) тільки 1, 3 і 4; б) тільки 2, 3 і 4; в) тільки 1, 2 і 3;
г) тільки 1; д) інша відповідь.
10.2.72. Які з оцінок не є оцінками дисперсії генеральної сукупності?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
а) тільки 1 і 3; б) тільки 1 і 4; в) тільки 2;
г) тільки 4; д) інша відповідь.
10.2.73. Інтервальною оцінкою параметра  розподілу генеральної сукупності з надійністю
розподілу генеральної сукупності з надійністю  є інтервал:
є інтервал:
а)  , для якого
, для якого 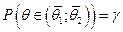 ;
;
б)  , для якого
, для якого  ;
;
в)  , для якого
, для якого  ;
;
г)  , для якого
, для якого  ; д) інша відповідь.
; д) інша відповідь.
10.2.74. Інтервальною оцінкою (надійним інтервалом) для математичного сподівання нормального розподілу з надійністю  є:
є:
а)  , якщо дисперсія
, якщо дисперсія  відома, де
відома, де 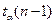 – квантиль порядку
– квантиль порядку  розподілу Стьюдента з
розподілу Стьюдента з  ступенем вільності (свободи);
ступенем вільності (свободи);
б)  , якщо дисперсія
, якщо дисперсія  невідома, де
невідома, де  – квантиль порядку
– квантиль порядку  стандартного нормального розподілу;
стандартного нормального розподілу;
в)  , якщо дисперсія
, якщо дисперсія  відома, де
відома, де  – квантиль порядку
– квантиль порядку  стандартного нормального розподілу;
стандартного нормального розподілу;
г)  , якщо дисперсія
, якщо дисперсія  невідома, де
невідома, де 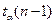 – квантиль порядку
– квантиль порядку  розподілу Стьюдента з
розподілу Стьюдента з  ступенем вільності (свободи);
ступенем вільності (свободи);
д) інша відповідь.
10.2.75. Інтервальною оцінкою (надійним інтервалом) з надійністю  для дисперсії нормального розподілу є (
для дисперсії нормального розподілу є ( 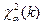 – квантиль порядку
– квантиль порядку  розподілу Пірсона (
розподілу Пірсона (  ) з
) з  ступенями вільності (свободи)):
ступенями вільності (свободи)):
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
10.2.76. Яке з тверджень щодо перевірки статистичних гіпотез є помилковим?
1) помилкою першого типу є відхилення правильної гіпотези;
2) помилкою другого типу є підтвердження неправильної гіпотези;
3) перевірка статистичної гіпотези є логічним доведенням її правильності чи хибності;
4) для кожної статистичної гіпотези існує альтернативна гіпотеза.
а) тільки 1; б) тільки 2; в) тільки 3;
г) тільки 4; д) інша відповідь.
10.2.77. Основна гіпотеза підтверджується, якщо вибіркове значення статистики критерію:
а) менше критичного значення;
б) більше критичного значення;
в) потрапляє в критичну область;
г) не потрапляє в критичну область;
д) інша відповідь.
10.2.78. Рівнем значущості критерію перевірки статистичної гіпотези є:
а) ймовірність того, що результат перевірки буде правильним;
б) ймовірність помилки першого роду;
в) ймовірність помилки другого роду;
г) максимальне відхилення вибіркового значення статистики критерію від критичного;
д) інша відповідь.
10.2.79. Критичним значенням критерію Пірсона перевірки гіпотези про розподіл генеральної сукупності при рівні значущості  є (
є (  – кількість інтервалів,
– кількість інтервалів,  – кількість параметрів розподілу оцінених за вибіркою):
– кількість параметрів розподілу оцінених за вибіркою):
а) квантиль порядку 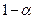 розподілу Пірсона (
розподілу Пірсона (  ) з
) з 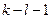 ступенем вільності (свободи);
ступенем вільності (свободи);
б) квантиль порядку  розподілу Пірсона (
розподілу Пірсона (  ) з
) з  ступенем вільності (свободи);
ступенем вільності (свободи);
в) квантиль порядку 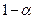 розподілу Пірсона (
розподілу Пірсона (  ) з
) з  ступенем вільності (свободи);
ступенем вільності (свободи);
г) квантиль порядку  розподілу Пірсона (
розподілу Пірсона (  ) з
) з 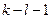 ступенем вільності (свободи);
ступенем вільності (свободи);
д) інша відповідь.
10.2.80. Які із тверджень правильні?
1) точковою оцінкою коефіцієнта кореляції випадкових величин  і
і  є
є  , де
, де  – вибіркове середнє значень величини
– вибіркове середнє значень величини  ,
,  – вибіркове середнє значень величини
– вибіркове середнє значень величини  ,
,  – вибіркове середнє значень величини
– вибіркове середнє значень величини  ,
,  та
та 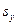 – вибіркові середньоквадратичні відхилення випадкових величин
– вибіркові середньоквадратичні відхилення випадкових величин  і
і  відповідно;
відповідно;
2) рівність нулю точкової оцінки коефіцієнта кореляції двох випадкових величин свідчить про їх некорельо-ваність;
3) відмінність від нуля точкової оцінки коефіцієнта кореляції двох випадкових величин свідчить про їх залежність;
4) вибірковий коефіцієнт кореляції лежить в межах від  до
до  .
.
а) тільки 2 і 3; б)тільки 3 і 4; в) тільки 1, 3 і 4;
г) тільки 1 і 4; д) інша відповідь.
10.2.81. Залежність випадкової величини  від значень невипадкової величини
від значень невипадкової величини  називається лінійною регресією
називається лінійною регресією  на
на  , якщо:
, якщо:
а)  ;
;
б) відхилення величини  від
від  є мінімальними;
є мінімальними;
в) середнє значення величини  при кожному значенні
при кожному значенні  дорівнює
дорівнює  ;
;
г) середнє значення величини  дорівнює
дорівнює 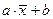 ;
;
д) інша відповідь.
10.2.82. Дисперсійний аналіз є методом перевірки гіпотези про:
а) рівність дисперсії генеральної сукупності даному числу;
б) рівність дисперсій кількох генеральних сукупностей;
в) рівність математичних сподівань кількох генеральних сукупностей;
г) задані значення математичних сподівань кількох генеральних сукупностей;
д) інша відповідь.
10.2.83. Нехай 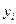 – результати спостережень за значеннями випадкової величини
– результати спостережень за значеннями випадкової величини  при значеннях
при значеннях  незалежної змінної
незалежної змінної  . Точкові оцінки параметрів лінійної регресії
. Точкові оцінки параметрів лінійної регресії  на
на  знаходимо із системи рівнянь:
знаходимо із системи рівнянь:
а) 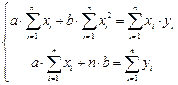 ; б)
; б)  ;
;
в)  ; г)
; г) 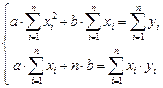 ;
;
д) інша відповідь.
10.2.84. Нехай  надійний інтервал з надійністю
надійний інтервал з надійністю  для параметра
для параметра  розподілу генеральної сукупності, причому
розподілу генеральної сукупності, причому  . Основна гіпотеза
. Основна гіпотеза 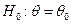 , альтернативна гіпотеза
, альтернативна гіпотеза  . В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості
. В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості  критерію?
критерію?
а)  ,
,  ; б)
; б)  ,
,  ;
;
в)  ,
,  ; г)
; г)  ,
,  ;
;
д) інша відповідь.
10.2.85. Нехай  надійний інтервал з надійністю
надійний інтервал з надійністю  для параметра
для параметра  розподілу генеральної сукупності, причому
розподілу генеральної сукупності, причому  . Основна гіпотеза
. Основна гіпотеза 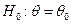 , альтернативна гіпотеза
, альтернативна гіпотеза  . В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості
. В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості  критерію?
критерію?
а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  ;
;
г)  ,
,  ; д) інша відповідь.
; д) інша відповідь.
Дата добавления: 2014-12-30; просмотров: 631; Мы поможем в написании вашей работы!; Нарушение авторских прав |