
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розділ 7 Тестові теоретичні завдання
1Які з наведених нижче тверджень є правильними?
2 Неперервність функції  в обмеженій замкненій
в обмеженій замкненій
області 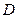 є достатньою умовою її інтегровності в цій області.
є достатньою умовою її інтегровності в цій області.
3 Обмеженість функції  в обмеженій замкненій області
в обмеженій замкненій області 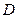 є необхідною умовою її інтегровності в цій області.
є необхідною умовою її інтегровності в цій області.
б) 2 і 3;
2 Які з наведених нижче тверджень є правильними?
2)Якщо функція  інтегровна в обмеженій замкненій області
інтегровна в обмеженій замкненій області 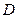 , то вона обмежена в цій області.
, то вона обмежена в цій області.
4)Якщо функція неперервна в обмеженій замкненій області 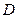 , то вона інтегровна в цій області.
, то вона інтегровна в цій області.
В) 2 і 4
3 Які з наведених нижче тверджень не є правильними ?
1) Для того, щоб функція  була інтегровною в області
була інтегровною в області 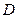 необхідно, щоб вона була неперервною в цій області.
необхідно, щоб вона була неперервною в цій області.
3) Для того, щоб функція  була інтегровною в області
була інтегровною в області 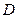 достатньо, щоб вона була обмеженою в цій області.
достатньо, щоб вона була обмеженою в цій області.
В) 1 і 3
4 Які з наведених нижче тверджень не є правильними ?
1)Для того, щоб функція  була інтегровною в обмеженій замкненій області
була інтегровною в обмеженій замкненій області 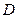 необхідно і достатньо, щоб функція була неперервною в цій області.
необхідно і достатньо, щоб функція була неперервною в цій області.
4)Для того, щоб функція  була інтегровною в обмеженій замкненій області
була інтегровною в обмеженій замкненій області 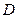 достатньо, щоб вона була обмеженою в цій області.
достатньо, щоб вона була обмеженою в цій області.
а) 1 і 4;
5 Які з наведених нижче рівностей справедливі для подвійного інтеграла ?
3)  ;
;
4)  (
( 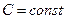 ).
).
Г) 3 і 4
6 Які з наведених нижче тверджень справедливі для подвійного інтеграла ?
1)Якщо в області 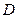 функція
функція  , то
, то  ;
;
2)Якщо область  , причому
, причому  і
і  не мають спільних внутрішніх точок, то
не мають спільних внутрішніх точок, то  ;
;
в) 1 і 2;
7 Якщо 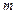 і
і  - відповідно найменше і найбільше значення функції
- відповідно найменше і найбільше значення функції  в області
в області 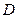 , а
, а  - площа цієї області, то має місце оцінка подвійного інтеграла:
- площа цієї області, то має місце оцінка подвійного інтеграла:
б)  ;
;
8 Середнім значенням функції  в області
в області 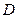 називається величина (
називається величина (  - площа області
- площа області 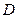 ):
):
б)  ;
;
Дата добавления: 2014-12-30; просмотров: 333; Мы поможем в написании вашей работы!; Нарушение авторских прав |