Изучение нового материала

В мире техники широкое применение находит алгебра логики. Рассмотрим, как применяется алгебра высказываний при конструировании устройств.

Задача. Пусть в некотором конкурсе решается вопрос о допуске того или иного участника к следующему туру тремя членами жюри: P, Q, R. Решение положительно тогда и только тогда, когда хотя бы двое членов жюри высказываются за допуск, причем среди них обязательно должен быть председатель жюри Q. Необходимо разработать устройство для голосования, в котором каждый член жюри нажимает на одну из двух кнопок – «За» или «Против», а результат голосования всех трех членов жюри определяется по тому, загорится(решение принято) или нет(решение не принято) сигнальная лампочка.

Формально это можно выразить так: требуется составить Функциональную схему устройства, которое на выходе выдавало бы 1, если участник допускается к следующему туру, и 0, если не допускается.

Решение:

Работу жюри можно легко представить в виде таблицы истинности:

Чтобы сконструировать устройство, мы должны знать:

· каким образом следует реализовать логические значения 0 и 1 в виде электрических сигналов на входе и выходе устройства;

· каким образом описать работу этого устройства: в виде формулы, схемы, таблицы истинности;

· существует ли алгоритм, позволяющий по известной таблице истинности построить схему устройства;

· из каких элементов должно состоять устройство.

Постановка подобных вопросов и поиск ответов на них привели к построению простейших преобразователей информации, составляющих основу любой вычислительной техники.

Использование алгебры логики высказываний в вычислительной технике

Средством обработки двоичных сигналов в ЭВМ являются логические элементы.

Логические элементы - это электронные схемы с одним или несколькими входами и одним выходом, через которые проходят электрические сигналы. Для реализации любых логических операций над двоичными сигналами достаточно элементов трех типов: НЕ, И, ИЛИ.

Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс - логическое значение сигнала 1, нет импульса— значение 0. На вход логических элементов поступают сигналы-аргументы, на выходе появляется сигнал-функция.

Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.

Логический элемент «НЕ»

Логический элемент «НЕ» (инвертор) выдает на выходе сигнал, противоположный сигналу на входе.

На вход Х логического элемента последовательно подаются два сигнала, на выходе получается последовательность из двух сигналов, значения которых определяются в соответствии с таблицей истинности логической инверсии.

Х

Физически это можно реализовать при помощи реле с нормально замкнутыми контактами.

Условное обозначение инвертора:

 

Логический элемент «И»

Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.

Х	Y	XÙY

 

Физически это можно реализовать последовательным соединением переключателей:

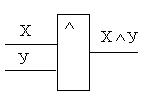Условное обозначение конъюнктора:

 

 

Логический элемент «ИЛИ»

Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов.

 

X	Y	XvY

 

 

Физически это можно реализовать параллельным соединением переключателей:

Условное обозначение дизъюнктора:

 

Наряду с инвертором, дизъюнктором и конъюнктором в логических схемах часто используются комбинированные логические элементы «И – НЕ» и «ИЛИ – НЕ», реализующие соответственно отрицание конъюнкции (элемент Шеффера) и отрицание дизъюнкции(элемент Вебба).

Условные обозначения:

«И – НЕ»	«ИЛИ – НЕ»