Тест: Логические высказывания. В-2

1. Признаками понятия обладает высказывание:

1) «Собеседник говорил громко»;

2) «Громко говорящий собеседник»;

3) «Говорите громко!»;

4) «Громкий голос раздражает».

2. «Если прошел снег, то на улице лето» - это суждение:

1) простое и истинное;

2) сложное и истинное;

3) простое и ложное;

4) сложное и ложное.

3. «Все ученики любят физику» - это суждение следующего типа:

1) простое и истинное;

2) сложное и истинное;

3) простое и ложное;

4) сложное и ложное.

4. Выбрать пример, не являющийся высказыванием:

1) «Никакая причина не извиняет невежливость»;

2) «Если совет разумен, то следует выполнить его»;

3) «Обязательно стань отличником»;

4) «Спортом заниматься полезно».

5. Из предложенных посылок:

«Все улетающие на юг птицы, называются перелетными»;

«Все грачи зимой улетают на юг» вытекает заключение:

1) «Все перелетные птицы - грачи»;

2) «Все птицы зимой живут на юге»;

3) «Грачи – перелетные птицы»;

4) «Некоторые грачи не живут зимой на юге».

6. Отрицанием высказывания

«Некоторые школьники предпочитают изучать китайский язык»

является высказывание:

1) «Некоторые школьники не предпочитают изучать китайский язык»;

2) «Некоторые школьники предпочитают изучать не китайский язык»;

3) «Неверно, что некоторые школьники предпочитают изучать китайский язык»;

4) «Неверно, что школьники предпочитают не изучать китайский язык».

7. Знаком 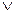в логике обозначается следующая операция:

1) инверсия; 3) дизъюнкция;

2) конъюнкция; 4) импликация.

8. Знаком в логике обозначается следующая операция:

1) конъюнкция; 3) импликация;

2) дизъюнкция; 4) эквиваленция.

9. Логическая операция с использованием ключевых слов «тогда и только тогда, когда . . .», называется:

1) конъюнкцией; 3) импликацией;

2) дизъюнкцией; 4) эквиваленцией.

10. Формулой логического высказывания

«Без Вас хочу сказать Вам много,

При Вас я слушать Вас хочу» является:

1) 3)

2) ; 4) .

Ответы: