
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тест: Логические высказывания. В-1
1. Признаками понятия обладает высказывание:
1) «Грачи прилетели»;
2) «Низко летающие птицы»;
3) «Птицы летают низко»;
4) «Грачи весну принесли».
2. «Наступил сентябрь, и начался учебный год» - это суждение:
1) простое и истинное;
2) сложное и истинное;
3) простое и ложное;
4) сложное и ложное.
3. «Все растенья съедобны» - это суждение следующего типа:
1) простое и истинное;
2) сложное и истинное;
3) простое и ложное;
4) сложное и ложное.
4. Выбрать пример, не являющийся высказыванием:
1) «Не можете ли вы передать соль?»;
2) «Гоголь писал «Мертвые души» в Риме»;
3) «Рукописи не говорят»;
4) «Некоторые лекарства опаснее самих болезней».
5. Из предложенных посылок:
«Память компьютера делится на внутреннюю и внешнюю»;
«Данная память не является внешней» вытекает заключение:
1) «Данная память не является внутренней»;
2) «Данная память является внутренней»;
3) «Данная память является внешней»;
4) «Данная память не делится».
6. Отрицанием высказывания
«Для каждого из нас учить второй иностранный язык легче, чем первый»
является высказывание:
1) «Не для каждого из нас учить второй иностранный язык легче, чем первый»;
2) «Для каждого из нас не учить второй иностранный язык легче, чем первый»;
3) «Неверно, что для каждого из нас учить второй иностранный язык легче, чем первый»;
4) «Неверно, что для каждого из нас учить второй иностранный язык не легче, чем первый».
7. Знаком ^ в логике обозначается следующая операция:
1) инверсия; 3) дизъюнкция;
2) конъюнкция; 4) импликация.
8. Знаком =>в логике обозначается следующая операция:
1) конъюнкция; 3) импликация;
2) дизъюнкция; 4) эквиваленция.
9. Логическая операция с использованием ключевых слов «Если . . . то . . .», называется:
1) конъюнкцией; 3) импликацией;
2) дизъюнкцией; 4) эквиваленцией.
10. Формулой логического высказывания
«Если у меня будет свободное время и не будет дождя, то я не буду писать сочинение, а пойду на дискотеку» является:
1)  3)
3) 
2) 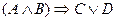 ; 4)
; 4)  .
.
Ответы:
Дата добавления: 2014-12-30; просмотров: 1071; Мы поможем в написании вашей работы!; Нарушение авторских прав |