Объяснение нового материала.

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1) подсчитать количество переменных n в логическом выражении;

2) определить число строк в таблице, которое равно m = 2ⁿ;

3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;

4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

5) заполнить столбцы входных переменных наборами значений;

6) провести заполнение таблицы истинности по столбцам.

Например: Для формулы A (B Ú 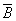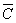) построить таблицу истинности.

1) Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³ = 8.

2) Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

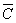
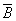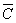
A	B	C				B Ú ( 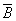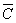)	A (B Ú )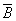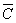

Если высказывание истинно при всех значениях входящих в него переменных, то такое высказывание называется тождественно истинным или тавтологией.

Если высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется тождественно ложным.

Если значения сложных высказываний совпадают на всех возможных наборах значений входящих в них переменных, то такие высказывания называются равносильными, тождественными, эквивалентными.