Декартова система координат

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.

Вектор назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.

Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат, называются осями координат.

1-я ось – ось абсцисс

2-я ось – ось ординат

3-я ось – ось апликат

Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А(x₁, y₁, z₁), B(x₂, y₂, z₂), то = (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Пример. Даны векторы (1; 2; 3), 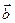(-1; 0; 3), 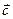(2; 1; -1) и 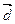(3; 2; 2) в некотором базисе. Показать, что векторы , 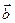и 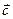образуют базис и найти координаты вектора 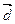в этом базисе.

Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

линейно независимы.

Тогда .

Это условие выполняется, если определитель матрицы системы отличен от нуля.

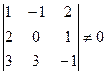
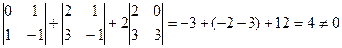
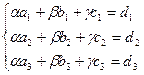
Для решения этой системы воспользуемся методом Крамера.

D₁=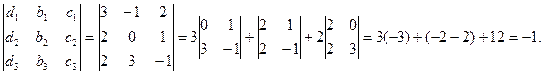

;

D₂ =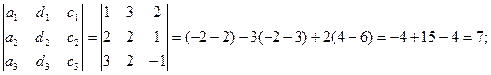

D₃ =

Итого, координаты вектора 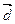в базисе , , 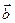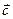: 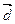{ -1/4, 7/4, 5/2}.

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то .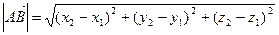

Если точка М(х, у, z) делит отрезок АВ в соотношении l/m, считая от А, то координаты этой точки определяются как:

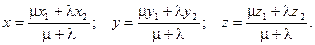
В частном случае координаты середины отрезка находятся как:

x = (x₁ + x₂)/2; y = (y₁ + y₂)/2; z = (z₁ + z₂)/2.