КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Энергия не исчезает и не возникает из ничего, а только превращается из одного вида в другой в строго эквивалентных соотношениях.
Впервые этот закон в 1842 г. сформулировал немецкий физик Ю. Мейер, врач по образованию.
В зависимости от вида системы I закон термодинамики имеет различные формулировки.
В изолированной системе внутренняя энергия постоянна (∆U = 0).
Для закрытой системы I закон термодинамики устанавливает связь между теплотой, полученной или выделенной системой в некотором процессе, изменением внутренней энергии системы и произведённой при этом работой.
Если к закрытой системе подвести теплоту Q, то эта энергия расходуется на увеличение внутренней энергии системы DU и на совершение системой работы против внешних сил окружающей среды:
Q = DU + А.
В изобарно-изотермических условиях, в которых функционируют живые организмы, совершаемая работа А = pDV, тогда:
Q = DU + pDV = (Uкон - Uнач) + (pVкон - pVнач) =
= (Uкон + pVкон) – (Uнач + pVнач)
Сумму внутренней энергии системы и произведения объёма на давление (U + pV) называют теплосодержанием или энтальпией*.
Энтальпия (Н)– термодинамическая функция, характеризующая энергетическое состояние системы при изобарно-изотермических условиях.
Раздел химии, занимающийся изучением тепловых эффектов химических реакций, называется термохимией.
Теплота, полученная системой при р, Т = const, равна приращению энтальпии системы DН:
Q = Hкон – Ннач = DН.
Абсолютное значение энтальпии, как и абсолютную величину внутренней энергии системы, определить невозможно, поэтому в термодинамических расчётах используют лишь изменение энтальпии, происходящее при переходе системы из одного состояния в другое. Величина DН не зависит от пути процесса, а определяется, как для любой другой функции состояния, разностью энтальпий, характеризующих конечное и начальное состояния системы:
DН = Hкон – Ннач.
Количество теплоты, которое выделяется или поглощается при прохождении химической реакции в изобарно-изотермических условиях, характеризуется изменением энтальпии системы и называется энтальпией реакции (DНр).
Химические реакции и физико-химические процессы подразделяются на экзотермические и эндотермические.
Экзотермические процессы сопровождаются выделением энергии из системы в окружающую среду.
В результате экзотермических процессов энтальпия системы уменьшается (Нкон < Hнач), следовательно:
DНэкзо = (Нкон - Hнач ) < 0.
Эндотермические процессы сопровождаются поглощением энергии системой из окружающей среды.
В результате эндотермических процессов энтальпия системы увеличивается (Hкон > Hнач), следовательно:
DНэндо = (Нкон - Hнач ) > 0.
Энтальпия системы является экстенсивным параметром и зависит от количества вещества, температуры и давления, поэтому изменение энтальпии в результате химической реакции или других процессов определяют при стандартных условиях.
Стандартные условия: количество вещества - 1 моль;
давление - 760 мм рт. ст. = 101 325 Па;
температура - 298 К ≈ 25 °С.
Термодинамические параметры и функции состояния системы или их изменения, измеренные при стандартных условиях, обозначаются соответствующим символом с верхним индексом "°". Стандартную энтальпию реакции обозначают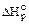 
, кДж/моль.
Стандартная энтальпия химической реакции представляет собой энергетическую характеристику реакции, проводимой при стандартных условиях. Химические уравнения, для которых указано значение энтальпии реакции, называются термохимическими уравнениями. Например, для реакции горения 1 моль ацетилена:
С2Н2(г) + 2,5О2(г) = 2СО2(г) + Н2О(г); 
= -1256 кДж/моль.
Кроме тепловых эффектов термохимические уравнения обязательно содержат индексы, обозначающие агрегатные состояния исходных веществ и продуктов реакции. Следует также иметь ввиду, что термохимические уравнения могут иметь дробные стехиометрические коэффициенты; это связано с тем, что тепловой эффект реакции рассчитывается только на 1 моль продукта реакции или на 1 моль одного из реагирующих веществ.
Для оценки энергетического состояния веществ в термодинамике используются значения стандартных энтальпий образования этих веществ, обозначаемые ∆Н°[вещество (агрегатное состояние)], кДж/моль.
Стандартная энтальпия образования простых веществ в их наиболее термодинамически устойчивом агрегатном и аллотропном состоянии при стандартных условиях принимается равной нулю.
Например, для кислорода DНо (О2) = 0, для графита 
(Сграфит) = 0. Однако стандартная энтальпия образования озона DHо (О3) = 142,2 кДж/моль, алмаза DНо (Салмаз) = 1,8 кДж/моль.
Стандартная энтальпия образования сложного вещества равна энтальпии реакции получения 1 моль этого вещества из простых веществ при стандартных условиях.
Например, стандартная энтальпия образования этанола равна стандартной энтальпии гипотетической реакции:
2Сграфит + 3Н2(г) + 0,5О2 (г) = С2Н5ОН(ж);
DНо (С2Н5ОН) = -277 кДж/моль.
Значение стандартной энтальпии образования сложного вещества зависит от природы вещества и его агрегатного состояния. Числовые значения стандартных энтальпий образования веществ приводятся в справочниках.
Энтальпию реакции можно определить как экспериментально, так и методом расчёта с использованием стандартных энтальпий образования веществ, участвующих в химической реакции, на основе закона, открытого российским учёным Г. И. Гессом (1840 г.).
Энтальпия реакции, то есть тепловой эффект реакции, зависит только от природы и состояния исходных веществ и конечных продуктов и не зависит от пути, по которому протекает реакция.
Закон Гесса является вполне строгим для процессов, происходящих при постоянном давлении или при постоянном объёме. Для этих процессов он может рассматриваться как частная форма выражения закона сохранения энергии применительно к химическим реакциям.
| Герман Иванович Гесс (7.VIII 1802—12.XII 1850). Русский химик, академик Петербургской АН (с 1830). Родился в Женеве 7 августа 1802 г. Окончил Дерлтский университет (доктор медицины, 1825). Совершенствовал образование в Стокгольмском университете (1825). С 1830 – профессор Петербургского технологического института, в 1832–1849 –Петербургского горного института. Один из основоположников термохимии. Значительно раньше J. П. Ю. Ю. Томсена и П. Э. М. Бертло выдвинул (1840) положение, согласно которому величины тепловых эффектов реакции могут служить мерой химического сродства. | 
|
Открыл (1840) основной закон термохимии – закон постоянства количества тепла, по которому тепловой эффект реакции зависит только от начального и конечного состояний реагирующих веществ, а не от количества стадий процесса (закон Гесса). Доказал (1842), что при смешении нейтральных солевых растворов тепловой эффект отсутствует (правило термонейтральности). Установил, что при нейтрализации грамм-эквивалента любой сильной кислоты сильным основанием всегда выделяется одинаковое количество тзп-ла (13,5 ккал). Открыл и определил (1830–1834) состав четырех новых минералов – вертита, уваровита, гидроборацита и фольбортита. Предложил (1833) способ получения теллура из теллурида серебра — минерала, который был им впервые изучен. Изучал (1832) окислы кобальта. Установил катализирующее и адсорбционное свойства мелкораздробленной платины. Одним из первых изучал состав кавказских нефтей. Открыл сахарную кислоту. Написал учебник «Основания чистой химии» (1831), выдержавший семь изданий.
В его честь теллурид серебра назван гесситом.
Закон Гесса можно проиллюстрировать следующей схемой:
Переход системы из начального состояния в конечное можно осуществить разными путями:
- непосредственно через реакцию, энтальпия которой равна DHр;
- в результате двухстадийного процесса через промежуточное состояние А, энтальпии отдельных стадий которого равны соответственно DH1 и DH2;
- через ряд реакций трёхстадийного процесса через промежуточные состояния В и С, для которых энтальпии отдельных стадий равны соответственно DH3, DH4 и DH5.
В соответствии с законом Гесса:
DHр = DH1 + DH2 = DH3 + DH4 + DH5.
В термохимических расчётах большое значение имеют следствия из закона Гесса.
Первое следствие. Энтальпия реакции равна разности алгебраической суммы энтальпий образования всех продуктов реакции и алгебраической суммы энтальпий образования всех исходных веществ:
DHр = ∑vкон DHкон (Yкон) - ∑vисх DHисх (Xисх),
где DH (Y), DH (X) - энтальпии образования продуктов реакции Y и исходных веществ X;
vкон. и vнач - соответствующие стехиометрические коэффициенты в уравнении химической реакции.
Например, для реакции образования хлороводорода
Н2 + Cl2 = НCl
энтальпия реакции по закону Гесса равна
DHр = 2DH (НCl) – [DH (Н2) + DH (Cl2)
Это следствие позволяет вычислять энтальпии различных реакций (в том числе и биохимических, осуществление которых in vitro* невозможно), используя табличные значения стандартных энтальпий образования продуктов реакции и исходных веществ.
Рассчитаем, например, энтальпию реакции получения мочевины в организме из аммиака и оксида углерода (IV):
2NH3(г) + СО2(г) = СО(NH2)2(т) + Н2О(г)
= [ 
(СО(NH2)2(т) + ( Н2О(г))] – [2 ( NH3(г) + ( СО2(г)) =
= (–333 – 242) – (–2 ∙ 46 – 394) = 89 кДж/моль.
Второе следствие Энтальпия прямой реакции численно равна энтальпии обратной реакции, но с противоположным знаком:
∆ 
= – ∆ 
.
Рассчитаем, например, стандартную энтальпию реакции фотосинтеза глюкозы, которая является обратной реакцией горения глюкозы:
6СО2(г) + 6Н2О(ж) 
С6Н12О6(т) + 6О2(г)
= – 
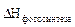(С6Н12О6(т)) = – 1273 кДж/моль.
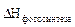(С6Н12О6(т)) = – (– 1273) = 1273 кДж/моль.
Основным источником энергии для живых организмов является химическая энергия, заключённая в продуктах питания. Для человека главными компонентами пищи являются жиры, углеводы и белки, окисление которых сопровождается выделением энергии. В медицине энергетическую характеристику продуктов питания принято выражать в калориях. Пища обычно представляет собой смесь питательных веществ сложного состава, поэтому калорийность пищи указывается в расчёте на 1 г, а не на 1 моль.
Калорийностью питательных веществ называется энергия, выделяемая при полном окислении (сгорании) 1 г питательных веществ.
Взаимосвязь между единицами энергии выражается соотношением: 1 калория = 4,18 Дж.
Согласно закону Гесса теплота, которая выделяется при окислении питательных веществ, не зависит от того, как или где они окисляются, конечно, при условии, что продукты реакции остаются неизменными. Жиры, углеводы и белки окисляются в организме до тех же продуктов, что и при сгорании в калориметре:
“С” 
СO2; “Н” Н2О; “N” N2*
Поэтому для энергетической оценки большинства продуктов питания может служить энтальпия реакции их сгорания. Наибольшую энергетическую ценность имеют жиры, при окислении которых выделяется 37,7–39,8 кДж/г (9,0–9,5 ккал/г). В процессе усвоения углеводов в организме человека выделяется 16,5–17,2 кДж/моль (4,0–4,1 ккал/г). На этом же уровне находится и калорийность белков: 16,5–17,2 кДж/г (4,0–4,1 ккал/г). Биоэнергетику организма можно регулировать не только при помощи выбора отдельных продуктов, но, главным образом, их сочетанием. Для взрослого человека суточная норма потребления составляет: жиров – 60–70 г, белков – 80–100 г (при тяжёлом физическом труде – 130–140 г), а потребляемая масса углеводов должна в 4–5 раз превышать массу белков, причём только небольшая часть от этого количества должна быть в виде сахарозы (около 8 г).
В основе научной диетологии лежит соответствие калорийности пищевого рациона энергозатратам человека. Суточная потребность человека в энергии составляет:
8 400–11 700 кДж (2 000-2 800 ккал) при лёгкой работе в сидячем положении (портные, канцелярские работники);
12 500–15 100 кДж (3 000–3 600 ккал) при умеренной и напряженной мышечной работе (учащиеся, студенты, врачи, рабочие-станочники);
16 700–20 900 кДж (4 000-5 000 ккал) при тяжёлом физическом труде (литейщики, кузнецы);
до 30 100 кДж (7 200 ккал) при особо тяжёлом труде (землекопы, косари, спортсмены).
Зная первый закон термодинамики, закон Гесса и его следствия, химический состав продуктов питания и энергетические характеристики питательных веществ, врач должен уметь с учётом профессии человека и на основе энергетического баланса его жизнедеятельности составить оптимальный рацион питания (энергоменю).
3. ПОНЯТИЕ О САМОПРОИЗВОЛЬНЫХ ПРОЦЕССАХ. ЭНТРОПИЯ
Одним из важнейших аспектов термодинамики является формулировка условий самопроизвольности протекания любых процессов.
Самопроизвольным (или спонтанным) является процесс, который совершается в системе без затраты работы извне и который уменьшает работоспособность системы после своего завершения.
Следовательно, самопроизвольно система может переходить только из менее устойчивого состояния в более устойчивое. На основе I закона термодинамики можно сформулировать один из важных принципов самопроизвольности протекания процессов в системе, заключающийся в стремлении системы к минимуму энергии за счёт выделения энергии в окружающую среду.
Этот энергетический принцип особенно важен для систем, которые можно рассматривать как единую частицу.
Например, капля дождя всегда самопроизвольно падает вниз, уменьшая при этом свою потенциальную энергию. Каплю воды необходимо рассматривать как совокупность очень большого числа молекул, когда происходит процесс её испарения, протекающий самопроизвольно, несмотря на то, что он эндотермический (требует поступления энергии из окружающей среды).
Следовательно, для описания условий протекания самопроизвольных процессов одного энергетического принципа недостаточно, особенно в системах, состоящих из большого числа частиц. Главное изменение, которое происходит при испарении капли, заключается в переходе системы из жидкого состояния (с частично упорядоченным состоянием частиц) в парообразное, в котором частицы не упорядочены. Таким образом, для описания движения в системах, содержащих большое число частиц, необходимо учитывать неупорядоченность расположения и движения этих частиц, то есть энтропию системы (разд. 1).
Значение энтропии как меры неупорядоченности системы зависит от агрегатного состояния и природы вещества, температуры, давления и сложности системы.
Энтропия вещества в газообразном состоянии больше, чем энтропия его в жидком состоянии, а последняя больше энтропии этого вещества в твёрдом состоянии:
S(г) > S(ж) > S(т).
Энтропия простых веществ зависит от их аллотропной формы:
S(Сграфит) > S(Салмаз); S(О2) < S(О3).
Энтропия системы при повышении температуры возрастает, так как увеличивается неупорядоченность движения частиц:
если Т2 > Т1, то S2 > S1.
Энтропия системы при повышении давления уменьшается, так как снижается неупорядоченность движения частиц:
если p2 > р1, то S2 < S1.
Энтропия системы с увеличением её сложности повышается, так как возрастает число видов частиц и вариантов их расположения.
Для энергетической характеристики вещества при стандартных условиях, наряду со стандартной энтальпией, используют стандартную энтропию вещества Sо. В отличие от стандартной энтальпии, стандартная энтропия простых веществ не равна нулю. Энтропия всех веществ всегда больше нуля.
В случае идеально упорядоченного кристалла при температуре 0 К его энтропия S = 0. Это даёт естественную нулевую точку отсчёта для значений энтропии (отсутствующую для ранее рассмотренных функций состояния U и Н) и позволяет измерить или теоретически рассчитать абсолютные значения энтропии. Поэтому перед символом энтропии вещества не ставят знак дельта (D). Значения энтропии для стандартных состояний веществ приведены в справочниках термодинамических величин.
Изменение стандартной энтропии в химической реакции ( 
) определяется разностью алгебраических сумм стандартных энтропии продуктов реакции Yкон. и исходных веществ Хисх. с учётом соответствующих стехиометрических коэффициентов:
DSр = ∑vкон DSкон (Yкон) - ∑vисх DSисх (Xисх),
где DS (Y), DS (X) - энтропии образования продуктов реакции Y и исходных веществ X;
vкон. и vнач.- соответствующие стехиометрические коэффициенты в уравнении химической реакции.
4. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ.
ЭНЕРГИЯ ГИББСА
Второй закон (второе начало) термодинамики определяет направленность и пределы протекания самопроизвольных процессов, в том числе и биохимических.
Рассмотрим изолированную систему, где исключён обмен энергией и веществом. Допустим, что в изолированной системе находятся два любых газа, например гелий Не и аргон Аr, которые не взаимодействуют между собой и не перемешаны. Естественно, эти газы будут самопроизвольно и необратимо смешиваться, а все свойства системы останутся без изменения, за исключением её энтропии. В исходном состоянии системы, когда газы ещё не смешались, её энтропия (Sнач) меньше, чем энтропия (Sкон)_ состояния после смешивания газов, характеризующегося неупорядоченностью расположения и движения молекул газов. Следовательно, в результате самопроизвольного необратимого процесса в изолированной системе её энтропия возросла: DS = Sкон - Sнач > 0. На основе этого сформулирован II закон термодинамики для изолированных систем.
Дата добавления: 2015-01-01; просмотров: 476; Мы поможем в написании вашей работы!; Нарушение авторских прав |