Оперативно-технічні характеристики системи

Найважливішою властивістю структури ТС є якість передачі інформації між елементами системи. Ця властивість характеризує здатність системи виконувати завдання зі своєчасного й достовірного доведення повідомлень. Цю властивість відображають наступні оперативно-технічні характеристики:

- якість передачі за критерієм імовірності втрати інформації ;

- надійність за критеріями ймовірності безвідмовної роботи та за ймовірністю доведення повідомлення ;

- своєчасність;

- достовірність передачі інформації за критеріями стійкості й живучості.

Окремим випадком якості передачі є якість обслуговування інформації, що надходить.

Кількісно цю характеристику можна виразити ймовірністю – ймовірністю втрати інформації під час її оброблення. Для знаходження цієї характеристики можна використати матричний метод Лазарєва, що дає можливість знайти найбільш надійний шлях – шлях з мінімальним значенням імовірності втрат повідомлень.

Припустимо, що найбільш надійний шлях – це шлях, у якому добуток ймовірностей 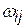справного стану окремих його ділянок має максимальну величину, тобто

, (1)

де k – довжина шляху (кількість транзитних ділянок n-го шляху ( ).

У прямій постановці така задача не має розв’язків. Однак, якщо зробити деякі нескладні перетворення вихідних даних, її можна звести до раніше розглядуваного матричного методу. Дійсно, замість виразу (1) можна записати:

,

де а – основа логарифмів (можна вибирати довільно).

Оскільки ймовірність і логарифм цієї величини – величина від’ємна, то можна скористатися іншою формою запису цільової функції:

, (2)

тому що величина .

Якщо тепер ребрам графа структури системи поставити у відповідність довжину , то завдання визначення найбільш надійного шляху зводиться до завдання пошуку шляху мінімальної довжини.

Це завдання легко розв’язується із застосуванням матричного способу визначення найкоротших шляхів, для чого спочатку складається матриця , а потім відповідно до матричного методу здійснюється її підняття до ступеню. Після цього отримані елементи дисперсійної матриці використовують для обчислення надійності окремих ребер структури системи:

, (3)

а надійність вибраного шляху визначають за формулою (1).

Ще одним параметром, який характеризує оперативно-технічні властивості ТС, є надійність. Надійність структури – це властивість, що відображає здатність системи виконувати поставлені завдання, зберігаючи в часі значення експлуатаційних показників у заданих межах. Ця характеристика визначається надійністю окремих елементів ТС, структурою і топологією, станом навколишнього середовища та ін. У зв'язку з цим кількісне оцінювання надійності вкрай ускладнене.

Щодо теорії надійності всі ТС системи мають такі особливості:

- показник надійності вкрай важко визначити для структури системи в цілому, тому що надійність функціонування різних її ребер і вершин неоднакова;

- показник надійності залежить від багатьох факторів, навіть від психофізичного стану оперативного персоналу, що обслуговує складні технічні системи;

- під час передачі по одних і тих самих ребрах різних повідомлень може змінюватися склад устаткування ребра відповідно до виду переданого повідомлення та ін.

Як відомо, надійність може характеризуватися ймовірністю безвідмовного функціонування . Увівши матрицю надійності , аналогічну матриці , можна одержати матричну форму запису величин надійності окремих ребер структури ТС.

Оцінку надійності структури системи можна отримати з матричної форми запису в такий спосіб. Параметри матриці суміжності поетапно перемножимо на величину , одержану з матриці надійності відповідних ребер. У цьому випадку добуток може набувати таких значень:

(4)

де – імовірність безвідмовної роботи ребра .

Тоді вираз для відносної зв’язності мережі перетвориться на вираз для оцінювання надійності:

. (5)

Аналіз структурної надійності дає можливість:

- виявити елементи, відмова яких може призвести до часткового або повного руйнування структури ТС;

- визначити елементи, резервування яких забезпечить досягнення заданої якості функціонування ТС.

Дослідження структурної надійності технічної системи дає можливість оцінити її ефективність за критерієм імовірності передачі повідомлення від вершини до вершини 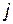при будь-яких алгоритмах її функціонування. Імовірність означає ймовірність наявності хоча б одного із заданої множини шляхів між елементами ТС (в цьому випадку між вершинами і 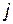). Найбільш широкого застосування набули елементні методи розрахунку ймовірності , що припускають самостійність елементів ТС та їхню функціональну незалежність.

На практиці фрагменти структури ТС можуть бути подані у вигляді послідовно-паралельних схем, розрахунок надійності яких досить простий. Так, якщо задано ймовірність доведення повідомлень елементарного (і-го) фрагмента шляху , то при послідовному з'єднанні елементів структури загальна ймовірність доведення інформації становить

, (6)

де n – кількість елементарних шляхів.

При паралельному з'єднанні n елементарних шляхів загальна ймовірність доведення повідомлень буде

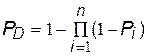. (7)

Розглянемо приклад, що демонструє можливість зведення елементарних структур ТС до послідовно-паралельних схем. На рис. 1 показано етапи перетворення графа вихідного фрагмента структури ТС для одержання кінцевого виразу оцінювання структурної надійності з використанням виразів (6) і (7). На графі 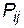– імовірність доведення повідомлень між вершинами i і j після відповідного етапу перетворення вихідного фрагмента структури системи.

На першому етапі перетворення оцінимо ймовірність доведення повідомлень між вершинами 1 і 3 через вершину 2, тобто визначимо . Скориставшись формулою (6), одержимо

.

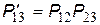Рис. 1. Етапи перетворення структури графа

На другому етапі отримуємо значення 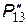з використанням виразу (7), тому що між вершинами 1 і 3 в еквівалентному графі є дві паралельні гілки, тобто

.

Аналогічно знаходимо . Остаточно маємо:

.

Після виконання всіх етапів перетворень вираз для оцінювання ймовірності доведення повідомлень між 1 і 4 вершинами ТС:

.

Часто ймовірності доведення повідомлень між елементами структури ТС приблизно однакові, тому для отримання наближених оцінок можна припустити, що 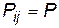. Тоді після проведення перетворень вираз для оцінювання ймовірності доведення повідомлень:

.

Інколи для спрощення розрахунків з метою одержання попередніх результатів, використовують замість точних методів нерівності, що дають можливість отримати верхню і нижню межі змінення показника надійності :

.

Для оцінювання структурної надійності розглянутий вище метод використовують із застосуванням дерева шляхів (для найбільш критичних шляхів структури).

Як уже зазначалося, якість передачі інформації між елементами ТС відображають такі оперативні характеристики, як своєчасність і достовірність.

Своєчасність – це оперативно-технічна характеристика, яка поряд з іншими показниками визначає швидкість доведення повідомлень від одного елемента ТС системи до іншого. Вона оцінюється за середньою величиною часу встановлення з'єднань через n транзитних вершин у структурі графа системи:

при . (8)

Якщо між вершинами є кілька можливих шляхів, то визначається той шлях, для якого ця величина – мінімальна.

Приклад. Для структури ТС, яку задано матрицею часу Т, оцінити швидкість доведення повідомлень від п’ятого елемента системи до третього:

.

Обчислимо довжину шляху між вершиною 5 та сусідніми з нею вершинами, скориставшись матрицею часу Т:

, ,

тобто шляхи мінімальної довжини проходить через вершини 1 і 4:

.

Обчислимо швидкість доведення повідомлень між вершиною 1 та сусідніми з нею вершинами:

, , , .

Мінімальний шлях становить

.

Обчислимо швидкість доведення повідомлень між вершиною 6 та сусідніми з нею вершинами:

, .

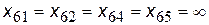Таким чином, швидкість доведення повідомлень між вершинами 5 і 3 буде

.

Із вершини 5 існує ще один шлях через вершину 4. Тому обчислимо швидкість доведення повідомлень між вершиною 4 та сусідніми з нею вершинами:

х₄₁=х₄₃=х₄₅=х₄₆=∞, .

Мінімальний шлях становить

.

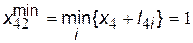Обчислимо швидкість доведення повідомлень між вершиною 2 та сусідніми з нею вершинами:

, .

Таким чином, згідно з виразом (3.35) мінімальна швидкість доведення повідомлень між вершинами 5 і 3 буде

.

Достовірність кількісно характеризується ступенем відповідності прийнятих даних переданим (іноді цю величину називають вірогідністю). Зниження достовірності передачі даних називають перекручуванням, що відбувається під впливом зовнішніх і внутрішніх (апаратурних) завад (перешкод). Здатність структури системи протистояти шкідливому впливу завад називають завадостійкістю. У зв'язку із цим важливими характеристиками є стійкість і живучість.

Стійкість передачі інформації в ТС характеризує здатність її структури зберігати свої властивості при впливі різних зовнішніх факторів.

Стійкість можна визначити кількісно за середнім часом відновлення нормального функціонування системи після різноманітних ушкоджень або змін її структури. У нормальних умовах функціонування ТС її стійкість – величина постійна, але якщо ж які-небудь фактори призводять до зміни структури ТС, а кількість цих змін в одиницю часу досягає деякої величини, значення починає різко зростати, що призведе до зниження стійкості. Ці процеси характеризує показник

. (9)

Характер залежності величини стійкості М від показано на рис. 2. Видно, що до певного значення =Ткр засоби ТС здатні успішно справитися з відновленням нормального функціонування. Коли ж кількість ушкоджень досягає критичної величини, роботи з відновлення затягуються, природно, зростає , а отже, зменшується стійкість структури ТС.

Значення так само заносять до матриці .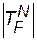

Під живучістю розуміється властивість структури ТС забезпечувати передачу інформації між абонентами (вершинами графа) під час впливу факторів, що заважають. В окремому випадку живучість характеризують показником структурної живучості або просто живучістю .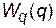

Показник живучості – це середня частка ребер графа, що зберігаються при одночасному ушкодженні q довільних областей графа структури .

У загальному випадку, якщо втрата окремих зв'язків рівно ймовірна, показник живучості структури системи можна виразити таким співвідношенням:

,

де A – кількість ребер вихідної структури ТС; q – кількість ребер, що вийшли із ладу; – частка втрачених зв'язків у структурі графа; – імовірність втрати цієї частки зв'язків, яка становить

,

де – кількість сполучень з А по q.

Тоді показник живучості матиме такий вигляд:

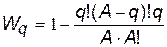, . (10)

Приклад.Оцінити живучість системи, структуру якої задано матрицею суміжності

,

за умови, що втрата окремих зв'язків у структурі системи рівноймовірна.

Структуру ТС у вигляді неорієнтованого графа зображено на рис. 3.

Визначимо всі значення коефіцієнта живучості для :

, ; , ;

, ; , ;

, ; , ;

, ; , .

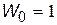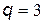Характеристику живучості структури для системи наведено на рис. 4.

Рис. 4. Залежність для системи

З точки зору оперативності виділяють ще дві характеристики: мобільність і пропускну здатність.

Мобільність – одна з найважливіших оперативних характеристик ТС типу мережі. Вона визначає здатність системи до своєчасного розгортання, нарощування й змінювання структури відповідно до обставин. Мобільність визначається за середнім часом розгортання .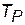

Пропускна здатність – це здатність ТС із заданою структурою забезпечити передачу заданого обсягуінформації з необхідною якістю за заданий час.