
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания. Тест 10.1. Интенсивность входящего потока заявок зависит от состояния системы для СМО
Тесты
Тест 10.1. Интенсивность входящего потока заявок зависит от состояния системы для СМО
1) с ожиданием
2) с отказами
3) с "нетерпеливыми" заявками
4) замкнутых
5) с ограниченным числом мест в очереди
Тест 10.1.Пассивное состояние источника заявок — это такое состояние, при котором поданная им последняя заявка
1) уже обслужена
2) стоит в очереди
3) находится под обслуживанием
Тест 10.1. Активное состояние источника заявок — это такое состояние, при котором поданная им последняя заявка
1) уже обслужена
2) стоит в очереди
3) находится под обслуживанием
Тест 10.1. В замкнутой одноканальной СМО, состояния системы нумеруют по числу источников, находящихся
1) в активном состоянии
2) в пассивном состоянии
3) в системе
Тест 10.1. В замкнутой СМО абсолютная пропускная способность равна произведению вероятности того, что
1) канал занят, на интенсивность потока обслуживании одним каналом
2) заявка будет обслужена, на интенсивность потока обслуживании одним каналом
3) заявка будет обслужена, на интенсивность входящего потока заявок
Тест 10.1. Для замкнутой СМО предельные вероятности состояний системы существуют при значениях трафика
1) любых
2) больших единицы
3) меньших единицы
Тест 10.1. Интенсивность входящего потока для замкнутой СМО с i источниками, каждый из которых с интенсивностью λ подает заявку на обслуживание в случае, когда k источников находятся в пассивном состоянии, равна
1) λ
2) iλ
3) kλ
4) (i – k)λ
11.Замкнутая многоканальная СМО
Рассмотрим теперь более общий, чем в предыдущем разделе, случай замкнутой СМО, состоящей из 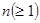 каналов обслуживания и
каналов обслуживания и  источников заявок. Как и в предыдущем разделе, каждый источник может находиться только в одном из двух состояний: активном или пассивном. Все время пребывания поданной источником последней заявки в системе (в очереди или под обслуживанием) источник находится в пассивном состоянии, в котором он не может послать следующей заявки. Как только поданная источником заявка будет обслужена, источник сразу же переходит в активное состояние, в котором он может послать следующую заявку. Каждый источник порождает простейший поток заявок с интенсивностью λ. Каждый канал порождает простейший поток обслуживании с интенсивностью μ. Нетрудно понять, что если бы число источников i не превышало числа каналов п, то это привело бы к существенному простаиванию каналов. Поэтому мы и полагаем i > п.
источников заявок. Как и в предыдущем разделе, каждый источник может находиться только в одном из двух состояний: активном или пассивном. Все время пребывания поданной источником последней заявки в системе (в очереди или под обслуживанием) источник находится в пассивном состоянии, в котором он не может послать следующей заявки. Как только поданная источником заявка будет обслужена, источник сразу же переходит в активное состояние, в котором он может послать следующую заявку. Каждый источник порождает простейший поток заявок с интенсивностью λ. Каждый канал порождает простейший поток обслуживании с интенсивностью μ. Нетрудно понять, что если бы число источников i не превышало числа каналов п, то это привело бы к существенному простаиванию каналов. Поэтому мы и полагаем i > п.
Пронумеруем состояния системы опять же по числу источников, пребывающих в пассивном состоянии, или что то же, — по числу заявок, находящихся в СМО (как в очереди, так и под обслуживанием):
s0 — все i источников находятся в активном состоянии, все п каналов свободны, очереди нет;
s1 — один источник находится в пассивном состоянии, один канал занят обслуживанием заявки, поданной этим источником, остальные i—1 источников находятся в активном состоянии, п – 1 каналов свободны, очереди нет;
s2 - два источника пребывают в пассивном состоянии, два канала заняты, i—2 источника в активном состоянии, п - 2 канала свободны, очереди нет;
sn — все п источников находятся в пассивном состоянии, все п каналов заняты, i— п источников в активном состоянии, очереди нет;
sn+i — п+1источников в пассивном состоянии, п каналов -заняты, одна заявка в очереди, i – (n+1) источников в активном состоянии;
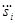 — все i источников в пассивном состоянии, п каналов заняты, i—n заявок в очереди.
— все i источников в пассивном состоянии, п каналов заняты, i—n заявок в очереди.
Граф состояний рассматриваемой СМО показан на рис. 11.1.
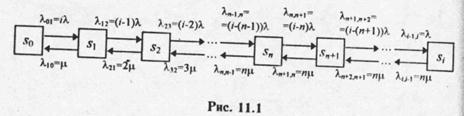 |
Из состояния Sk -i в состояние sk (k=1, …, i) систему переводит суммарный поток заявок, слагающийся из потоков заявок всех i — (k-1) источников, находящихся в активном состоянии; поэтому
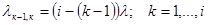 (11.1)
(11.1)
Из состояния sk в состояние sk-1, k = n+1, ..., i, СМО переходит под воздействием суммарного потока обслуживании, слагающегося из п потоков обслуживании на каждом из n занятых каналов (в состоянии sk, k=n+1, ..., i) с интенсивностью μ; следовательно,
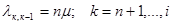 (11.2)
(11.2)
Из состояния sк в состояние sк-1, k = 1, ..., п, систему переводит суммарный поток обслуживании, слагающийся из k потоков обслуживании на каждом из k занятых каналов в состоянии sк с интенсивностью μ; стало быть
 (11.3)
(11.3)
В системе, как видно из графа состояний на рис. 11.1, протекает процесс гибели и размножения.
Для нахождения предельных вероятностей состояний найдем сначала по формуле (3.21) коэффициенты αk, k = 1, ..., i, для чего в (3.21) подставим выражения плотностей вероятностей переходов λk-1, k и λk, k-1, k =1, ..., i, по формулам (11.1) -(11.3):
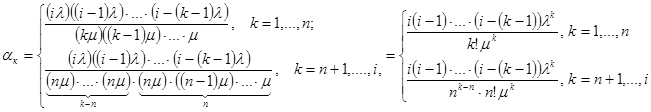
Используя обозначение р = λ/μ, получим:
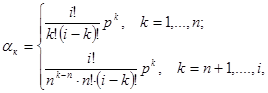
Найденные значения αk, k = 1, ..., i, подставим в формулы (3.19) и (3.20), заменив в последних п на i; в результате получим выражения для вероятностей состояний:
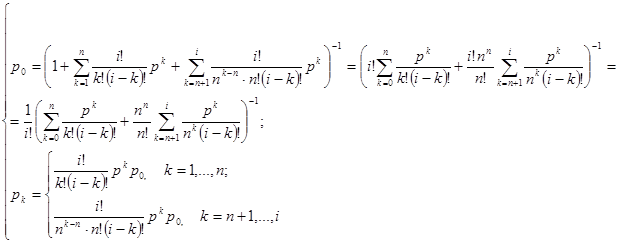 (11.4)
(11.4)
Легко убедиться в том, что формулы (11.4) при п = 1 превращаются в формулы для вероятностей состояний одноканальной замкнутой СМО, выведенные в разделе 10 (см. строки 3 и 4 табл. 10.2).
Пусть Nоб — дискретная случайная величина, представляющая собой число заявок, находящихся под обслуживанием, или что то же, число К занятых каналов. Очевидно, что закон распределения этой случайной величины имеет вид:
| Nоб = К | … | n - 1 | n | ||
| P | P0 | P1 | … | Pn-1 | Pn+Pn+1+…+Pi |
Поэтому, определяя среднее число 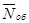 заявок, находящихся под обслуживанием, как математическое ожидание M[Nоб] случайной величины
заявок, находящихся под обслуживанием, как математическое ожидание M[Nоб] случайной величины 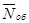 , и используя нормировочное условие и формулы (11.4), получим:
, и используя нормировочное условие и формулы (11.4), получим:
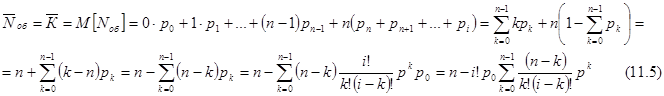
Так как 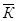 — среднее число занятых каналов, а μ- интенсивность потока обслуживании каждым каналом (среднее число обслуженных каждым каналом заявок за единицу времени), то абсолютная пропускная способность СМО (среднее число заявок, обслуживаемых всеми занятыми каналами за единицу времени), выражается следующей формулой
— среднее число занятых каналов, а μ- интенсивность потока обслуживании каждым каналом (среднее число обслуженных каждым каналом заявок за единицу времени), то абсолютная пропускная способность СМО (среднее число заявок, обслуживаемых всеми занятыми каналами за единицу времени), выражается следующей формулой
А = 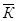 μ (11.6)
μ (11.6)
Интенсивность выходящего потока v = А = 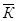 μ.
μ.
Поскольку каждая заявка, поступившая в СМО, будет обслужена, то относительная пропускная способность СМО Q = 1.
Рассуждая так же, как и в предыдущем разделе, мы найдем, что
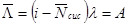 (11.7)
(11.7)
где 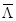 — средняя интенсивность среднего суммарного входящего потока, порождаемого средним числом i —
— средняя интенсивность среднего суммарного входящего потока, порождаемого средним числом i — 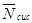 активных источников,
активных источников, 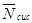 - среднее число заявок, находящихся в системе, т.е. в очереди и под обслуживанием, или, другими словами, среднее число
- среднее число заявок, находящихся в системе, т.е. в очереди и под обслуживанием, или, другими словами, среднее число  источников, находящихся в пассивном состоянии.
источников, находящихся в пассивном состоянии.
Так же, как и в разделе 10, можно показать, что средняя интенсивность 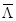 входящего потока есть математическое ожидание М[Λ] дискретной случайной величины Λ, принимающей значения Λ(k) = (i—k)λ, k = 0, 1, ..., i, представляющие собой интенсивности входящего потока, когда СМО находится в состоянии sk:
входящего потока есть математическое ожидание М[Λ] дискретной случайной величины Λ, принимающей значения Λ(k) = (i—k)λ, k = 0, 1, ..., i, представляющие собой интенсивности входящего потока, когда СМО находится в состоянии sk:
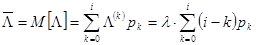
Подставляя формулу (11.6) в формулу (11.7), получаем
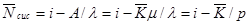 (11.8)
(11.8)
С другой стороны, среднее число  =
= 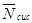 , источников в пассивном состоянии представляет собой математическое ожидание М[Nпас] случайной величины Nnac - числа источников в пассивном состоянии:
, источников в пассивном состоянии представляет собой математическое ожидание М[Nпас] случайной величины Nnac - числа источников в пассивном состоянии:
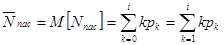 (11.9)
(11.9)
Вычитая из среднего числа 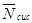 (см. равенство (11.8)) заявок, находящихся в СМО, среднее число
(см. равенство (11.8)) заявок, находящихся в СМО, среднее число 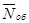 заявок под обслуживанием, найдем среднее число заявок в очереди:
заявок под обслуживанием, найдем среднее число заявок в очереди:
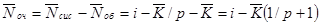
Среднее число заявок в очереди 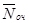 можно подсчитать и как математическое ожидание M[Nоч] дискретной случайной величины Nоч, представляющей собой число заявок в очереди.
можно подсчитать и как математическое ожидание M[Nоч] дискретной случайной величины Nоч, представляющей собой число заявок в очереди.
Если СМО находится в состоянии sk, k = 0, 1, ..., n, то в очереди нет заявок и, следовательно, NоЧ = 0 с соответствующей вероятностью pk, k = 0, 1, ..., n.
Если СМО находится в состоянии sk, k =n+1, ..., i, то в очереди Nоч = k—n заявок с вероятностью рк (k = n+1, ..., i).
Таким образом, закон распределения случайной величины Nоч имеет вид:
| Nоч | … | … | i - n | |||||
| P | P0 | P1 | … | pn | Pn+1 | Pn+2 | … | pi |
и потому
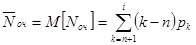
Нетрудно показать, что правая часть этого равенства совпадает с разностью 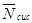 -
- 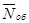 .В самом деле, по формуле (11.9) и определению
.В самом деле, по формуле (11.9) и определению 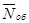 имеем:
имеем:
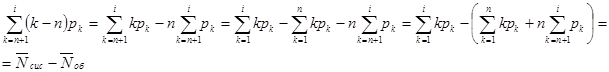
Таким же образом, как и в разделе 10, можно показать, что коэффициент готовности

откуда, применяя нормировочное условие и формулы (11.9), (11.8), (11.6) и (11.7), получаем
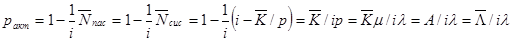
Формулы, полученные для 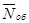 ,
, 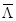 ,
, 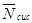 ,
, 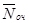 и pакт, превращаются при n = 1 в соответствующие формулы для одноканальной замкнутой СМО, выведенные в разделе 10.
и pакт, превращаются при n = 1 в соответствующие формулы для одноканальной замкнутой СМО, выведенные в разделе 10.
Можно найти вероятность робтого, что поступившая заявка немедленно будет принята к обслуживанию. Рассуждая таким же образом, как и в предыдущем разделе, мы найдем вероятность 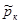 (k = 0, 1, ..., i—1) того, что в момент поступления заявки система находилась в состоянии sk:
(k = 0, 1, ..., i—1) того, что в момент поступления заявки система находилась в состоянии sk:
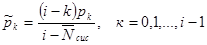 (11.10)
(11.10)
где рк (k = 0, 1, ..., i—1) определяются формулами (11.4), а 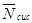 - формулой (11.8) или (11.9). Поступившая заявка тут же будет принята к обслуживанию, если в момент ее поступления СМО находилась в одном из состояний s0, s1, ..., sn-1, поскольку в каждом из них не все п каналов заняты. Поэтому, используя формулы (11.10) и (11.4), получаем:
- формулой (11.8) или (11.9). Поступившая заявка тут же будет принята к обслуживанию, если в момент ее поступления СМО находилась в одном из состояний s0, s1, ..., sn-1, поскольку в каждом из них не все п каналов заняты. Поэтому, используя формулы (11.10) и (11.4), получаем:
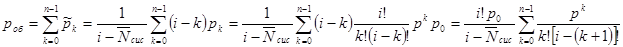
Событие, состоящее в том, что пришедшая заявка встанет в очередь, является противоположным событию, состоящему в том, что пришедшая заявка тут же будет принята к обслуживанию. Следовательно, вероятность того, что поступившая заявка встанет в очередь, роч можно вычислить по формуле:
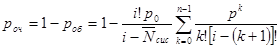
С другой стороны, пришедшей заявке придется встать в очередь и ожидать начала обслуживания только в том случае, если она пришла в момент, когда СМО находилась в одном из состояний sn, sn+1, ..., si-1 и потому, используя формулы (11.10) и (11.4), получаем другую формулу для вычисления роч:
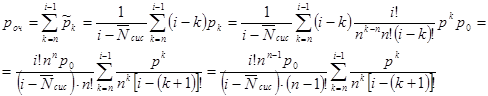
Выведем формулу для среднего времени 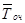 ожидания заявки в очереди.
ожидания заявки в очереди.
Для этого рассмотрим случайную величину 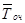 — время ожидания заявки в очереди и i несовместных гипотез Hk, k = 0, 1, ..., i—1, состоящих (как и в разделе 10) в том, что i момент поступления заявки СМО находилась в состоянии sk. При условии появления одной из этих гипотез может произойти событие Е, заключающееся в том, что на элементарном участке времени (t, t+dt) появилась заявка. Условные вероятности р(Hk|Е) гипотез Hk, k = 0, 1, ..., i—1, при условии, что событие Е уже наступило, равны
— время ожидания заявки в очереди и i несовместных гипотез Hk, k = 0, 1, ..., i—1, состоящих (как и в разделе 10) в том, что i момент поступления заявки СМО находилась в состоянии sk. При условии появления одной из этих гипотез может произойти событие Е, заключающееся в том, что на элементарном участке времени (t, t+dt) появилась заявка. Условные вероятности р(Hk|Е) гипотез Hk, k = 0, 1, ..., i—1, при условии, что событие Е уже наступило, равны 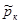 .
.
Заявка, поступившая в СМО при одной из гипотез Hk, k = 0, 1, ..., п—i, т.е. когда система находилась в одном из состояний Sо, S1, ..., Sn-1, в каждом из которых не все каналы заняты, сразу попадает под обслуживание и в очереди не стоит. Поэтому условное математическое ожидание M[Точ|Hk], k = 0, 1, ..., n—1, случайной величины Точ при гипотезе Hk равно нулю: M[Tоч|Hk] = 0, k = 0, 1, ..., n—1.
Если заявка приходит в систему при гипотезе Hn, т.е. когда СМО находится в состоянии Sn, в котором все п каналов заняты, то она становится в очередь и ждет освобождения одного из п каналов. Поскольку интенсивность обслуживании каждым каналом равна μ, то суммарный поток обслуживании всех n каналов будет иметь интенсивность пμ. Следовательно, заявке в очереди придется ждать среднее время обслуживания заявки всеми п каналами, равное 1/nμ. Поэтому M[Tоч|Hn+1] = 1/nμ.
Заявка, поступившая в систему, при гипотезе Hn+1, т.е. когда СМО находится в состоянии sn+1, в котором все я каналов заняты и одна заявка уже в очереди, становится в очередь и ожидает среднее время, равное 2/nμ, складывающееся из среднего времени 1/nμ обслуживания заявки, находящейся под обслуживанием, и среднего времени 1/nμ обслуживания заявки из очереди. Значит, М[ТОЧ1 Нn+1]=2/nμ .
И так далее.
Наконец, для заявки, поступившей в систему при гипотезе Hi-1, будем иметь:
M[Tоч|Hi-1] = (i-n)/nμ.
Следовательно, среднее время 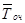 заявки в очереди
заявки в очереди

Подставив сюда выражения вероятностей 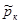 по формулам ,(11.10), найдем
по формулам ,(11.10), найдем
 (11.11)
(11.11)
При п = 1 из формулы (11.11) получаем формулу (10.10).
Для многоканальных замкнутых систем также имеет место формула (10.11). Действительно, в силу формул (11.4) и (11.7) из формул (11.11) получим:
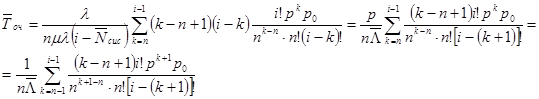
В сумме в правой части этого равенства сделаем замену индекса суммирования k + 1 = j, а затем индекс j заменим на k:
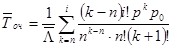
откуда, используя (11.4), получим:
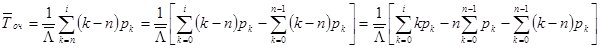
Отсюда, в силу равенства (11.9) и нормировочного условия,

Наконец, по определению среднего числа 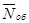 заявок, находящихся под обслуживанием (см. промежуточные выкладки формулы (11.5)), и среднего числа
заявок, находящихся под обслуживанием (см. промежуточные выкладки формулы (11.5)), и среднего числа 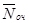 заявок в очереди, получим требуемое соотношение:
заявок в очереди, получим требуемое соотношение:
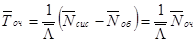 (11.12)
(11.12)
Используя формулы (11.6) и (11.7), получаем аналогичную формулу для среднего времени обслуживания заявки:
 (11.13)
(11.13)
Среднее время 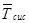 пребывания заявки в системе складывается из среднего времени ожидания заявки в очереди
пребывания заявки в системе складывается из среднего времени ожидания заявки в очереди 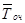 и среднего времени обслуживания заявки
и среднего времени обслуживания заявки 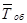 , поэтому из формул (11.12) и (11.13):
, поэтому из формул (11.12) и (11.13):

Так же, как и в предыдущем разделе, считаем, что источник в активном состоянии совершает некоторую полезную работу с производительностью l, а в пассивном состоянии он "не работает". Тогда используя формулу (11.8), можем найти среднюю производительность среднего числа источников в активном состоянии  . Она равна
. Она равна
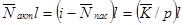
А средняя потеря производительности за счет источников, находящихся в пассивном состоянии, составит
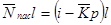
Выпишем параметры и характеристики СМО в табл. 11.1 и 11.2.
Таблица 11.1
Дата добавления: 2015-01-01; просмотров: 518; Мы поможем в написании вашей работы!; Нарушение авторских прав |