
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Агрегат-оператор
Агрегати-оператори – це агрегати, що виконують функції встановлення відношень між елементами, що агрегуються. До них належать: класифікатори, оператори-функції та статистики.
В умовах розвитку інформаційних і телекомунікаційних технологій, а також постійно зростаючих обсягів інформації, що циркулює в різних ТС, особливо в автоматизованих системах керування, під час синтезу слід враховувати такі особливості: великі обсяги інформації, які зазвичай надходять у систему паралельно, дублювання інформації, що надходить від різних систем і датчиків, формуючих інформацію щодо стану об’єкту керування, надмірність даних та ін. Все це ускладнюється тім, що сукупність даних, з якими доводиться мати справу, занадто численна і погано доступна для огляду, а для людини характерним є прагнення систематизувати великий обсяг даних, щоб “навести порядок” у своєму сприйнятті цієї різноманітності.
Для систематизації такого обсягу даних найчастіше використовується класифікація.
Класифікація – система супідрядних понять (класів, явищ, об'єктів) у деякій галузі знання, складена з урахуванням загальних ознак об'єктів і закономірностей зв'язків між ними.
Алгоритм одержання класифікацій під час агрегування даних для автоматизованих систем керування передбачає таку послідовність дій.
Крок 1. Формування єдиного масиву даних щодо об'єкта керування  із даних, що надходять від різних систем і датчиків, і формування інформації про стан цього об'єкта, тобто
із даних, що надходять від різних систем і датчиків, і формування інформації про стан цього об'єкта, тобто
 ,
,
де  – єдиний масив даних про об'єкт керування;
– єдиний масив даних про об'єкт керування;  ,
,  ,
,  – масиви даних, що формують інформацію про стан об'єкта. При цьому залежно від типу системи керування, кількість систем і датчиків, що формують цю інформацію, може бути різна.
– масиви даних, що формують інформацію про стан об'єкта. При цьому залежно від типу системи керування, кількість систем і датчиків, що формують цю інформацію, може бути різна.
Крок. 2. Виключення із масиву  інформації, що дублюється. Формування множини даних
інформації, що дублюється. Формування множини даних  , що не дублюються, тобто
, що не дублюються, тобто
 .
.
Крок 3. Групування об'єктів, характеристики яких збігаються за певними параметрами, формування множини одиночних і групових параметрів  .
.
Крок 4. Агрегування даних про об'єкт керування за певними параметрами, відповідно до запитів особи, що приймає рішення, з урахуванням поставлених завдань керування.
Найпростіший спосіб агрегування полягає у встановленні відношень еквівалентності між елементами, тобто в утворенні класів – розподілі досліджуваних об'єктів залежно від їхніх загальних ознак.
Підходи до виділення класів моделей можуть бути різними, в загальному випадку якщо подати клас як результат дії агрегату-оператора, то він матиме такий вигляд [1]:
ЯКЩО (умови на ознаки, що агрегуються), ТО (ім'я класу).
Класифікація є важливим багатофункціональним і багатобічним явищем у системному аналізі. Однак агрегування у класи – це ефективна, але зовсім не тривіальна процедура. Це зумовлено такими причинами:
1. Складність класифікації різко зростає, якщо ознака класифікації не спостерігається безпосередньо, а є агрегатом непрямих ознак.
| Приклад | Типове завдання діагностики захворювань за результатами обстеження – діагноз хвороби (її назвою є ім'я класу), який являє собою сукупність її симптомів і характеристик станів організму. |
2. За наявності ознаки належності до класу на практиці частіше виникає питання надійності й правильності класифікації.
| Приклад | Розкласти кольорові шматки картону за кольорами може бути складним завданням. Наприклад, до якого класу віднести помаранчевий шматок – до класу “червоні” чи “жовті”, якщо між ними немає інших класів. Якщо безпосередньо спостережувана ознака належить до класу, що формулюється природною мовою, то деяка невизначеність стає неминучою, наприклад у випадку, коли треба вирішити, кого віднести до класу “високі люди”. |
Інший тип агрегату-оператора виникає, якщо ознаки, що агрегуються, фіксуються на числових шкалах. Існують такі шкали:
1. Абсолютна шкала, результатом вимірювання за якою є число, що виражає кількість елементів у множині. У цій шкалі початок відліку й одиниці виміру – незмінні. Із числами, отриманими за такою шкалою, можна здійснювати будь-які арифметичні операції – всі ці дії будуть осмисленими.
2. Шкала відношень, у якій початок відліку – незмінний, а одиниці виміру можна масштабувати (наприклад, шкали для виміру маси, довжини і т.д.).
3. Шкала інтервалів, за якою можна змінювати початок відліку і одиниці виміру, наприклад, шкали для вимірювання температури (Цельсій, Кельвін, Фаренгейт), тиску, інтервалів часу й т.д.
| Приклад | Шкали відношень та інтервалів набули поширення у кваліметрії (від лат. qualismetro) – науці, що вивчає й реалізує методи кількісного оцінювання якості. Вони використовуються під час порівняльного оцінювання показників якості зразків нових виробів з базовими (еталонами). Урахування динаміки якості здійснюється таким чином: - якщо використовується шкала інтервалів, то при порівнянні різниця між базовим значенням і значенням, що порівнюється з ним, береться зі знаком “-“ при такому значенні показника, що приводить до підвищення якості, зі знаком “+” – у протилежному випадку; - якщо використовується шкала відношень, то відношення числових значень показників якості складається так, щоб при підвищенні їхньої якості порівняно з показником базового зразка воно було більшим від одиниці, при зниженні їхньої якості – меншим від одиниці. |
4. Шкала порядку, за допомогою якої одержують інформацію про те, у якому порядку об'єкти йдуть один за одним відповідно до деякої властивості. Прикладом можуть бути шкали, за якими виміряються твердість матеріалів, “подібність” об'єктів. До цієї групи шкал належить більшість шкал, які використовуються під час соціологічних і психологічних досліджень. Окремим випадком шкал порядку є бальні шкали, що використовуються під час зарахування абітурієнтів до вишів.
5. Шкала найменувань (номінальна), у якій числа використовуються виключно з метою позначення об'єктів. Крім порівняння на збіг, будь-які арифметичні дії над числами, що позначають імена об'єктів, є безглуздими. За допомогою шкал найменувань часто зазначають, чи є якась ознака в об'єкті.
Серед перелічених шкал абсолютна шкала є найбільш “сильною”, а шкала найменувань – найбільш “слабкою”.
Однак використовувати тільки абсолютні шкали не завжди доцільно. Для одержання інформації про властивості, що вимірюються “сильними” шкалами, потрібні більш досконалі вимірювальні прилади й процедури. У деяких випадках таких приладів і процедур може просто не бути.
| Приклад | Можна з'ясувати, чого певній людині хочеться більше – чаю чи кави, але визначити, наскільки більше і у скільки разів, важко. |
Отже, якщо агрегат-оператор дає можливість задати відношення на множині ознак у вигляді числової функції багатьох змінних, виражених у деякій шкалі, то його називають агрегатом-функцією. Окремим випадком агрегату-функції є випадок переходу від багатокритеріальної задачі до однокритеріальної за допомогою агрегування декількох критеріїв в один суперкритерій.
Багатокритеріальність характеризується наявністю багатьох кількісних показників  одні з яких бажано перетворити на максимум, інші – на мінімум. Однак розв’язок, що перетворює на максимум деякий показник зазвичай інші не перетворює ні на максимум, ні на мінімум. Тому найчастіше багатокритеріальну задачу зводять до однокритеріальної таким чином: “узагальнений” суперкритерій (функцію від всіх показників) подають у вигляді дробу, у чисельнику якого знаходяться величини, збільшення яких бажане, а в знаменнику – величини, збільшення яких небажане
одні з яких бажано перетворити на максимум, інші – на мінімум. Однак розв’язок, що перетворює на максимум деякий показник зазвичай інші не перетворює ні на максимум, ні на мінімум. Тому найчастіше багатокритеріальну задачу зводять до однокритеріальної таким чином: “узагальнений” суперкритерій (функцію від всіх показників) подають у вигляді дробу, у чисельнику якого знаходяться величини, збільшення яких бажане, а в знаменнику – величини, збільшення яких небажане
Різновидом такого суперкрітерію в задачах з різною розмірністю є вираз вигляду
 (
(  ), (1)
), (1)
де  ,
,  – мінімальне і максимальне значення
– мінімальне і максимальне значення 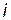 -ї характеристики системи;
-ї характеристики системи;  – кількість характеристик системи, необхідних для її дослідження.
– кількість характеристик системи, необхідних для її дослідження.
Такий підхід має один суттєвий недолік: перехід від багатокритеріальної задачі до однокритеріальної базується на неявному допущенні, що недолік в одному показнику може бути скомпенсований за рахунок іншого, що зазвичай не має місце.
| Приклад | Л. Толстой запропонував критерій оцінювання людини. Цей критерій мав вигляд дробу, у чисельнику якого знаходяться дійсні позитивні якості людини, а в знаменнику – його думка щодо себе. З першого погляду такий підхід є логічним. Однак уявимо собі людину, що майже зовсім не має позитивних якостей і зовсім без марнославства. За критерієм Л. Толстого, така людина повинна мати нескінченно більшу цінність, із чим ніяк не можна погодитися. |
Часто застосовують інший спосіб складання узагальненого критерію – подають його у вигляді “зваженої суми” частинних критеріїв, до якої кожний  входить з деякою “вагою”
входить з деякою “вагою”  (
(  ), що відбиває його важливість:
), що відбиває його важливість:
 , (2)
, (2)
де  – додатні коефіцієнти для тих критеріїв, значення яких треба збільшити, від’ємні – для критеріїв, які треба зменшити.
– додатні коефіцієнти для тих критеріїв, значення яких треба збільшити, від’ємні – для критеріїв, які треба зменшити.
Цей підхід набув широкого застосування під час оцінювання рівня якості виготовлення продукції – характеристики якості, що встановлює ступінь відповідності фактичних значень показників якості виготовленої продукції вимогам нормативно-технічних документів.
Приклад 1. Оцінити технічний рівень якості часів. Відомо, що технічний рівень часів характеризує “оцінне число”, що включає такі характеристики: відносний показник ізохромної похибки  (визначення точності ходу при різній величині заведення часів); відносний показник позиційної похибки
(визначення точності ходу при різній величині заведення часів); відносний показник позиційної похибки 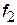 (визначення точності ходу при різному просторовому положенні часів); відносний показник температурної похибки
(визначення точності ходу при різному просторовому положенні часів); відносний показник температурної похибки 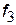 . Значення цих показників якості наведено в табл.1.
. Значення цих показників якості наведено в табл.1.
Знайдемо значення показників якості часів при порівнянні їх з показниками якості базового зразка за шкалою відношень. Відносний показник якості визначимо за формулою (відповідно до правила формування відносних показників, наведеним вище)
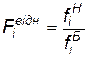 ,
,
де  ,
,  – числові значення показника якості нових часів і показника якості базового зразка відповідно.
– числові значення показника якості нових часів і показника якості базового зразка відповідно.
Результати порівняння показників якості зазначено у відповідному стовпці таблиці, причому частина значень відносних показників якості більша від одиниці, а решта – менша від одиниці, тобто однозначного висновку щодо якості нових часів зробити не можна.
Таблиця 1
Вихідні дані
| Відносний показник якості | Числове значення показника 
| Коефіцієнти 
| Значення відносного показника якості | |
| Годинник | Базовий зразок | |||
| Показник ізохромної похибки, с | 0,12 | 0,18 | 0,12 | 1,5 |
| Показник позиційної похибки, с | 0,15 | 0,17 | 0,08 | 1,13 |
| Показник температурної похибки, с | 0,3 | 0,28 | 0,8 | 0,93 |
Для оцінювання технічного рівня часів скористаємося формулою (2):
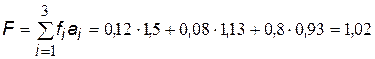 .
.
Отже, відповідно до правила формування відносних критеріїв якості технічний рівень оцінюваних часів вищий, ніж технічний рівень базового зразка.
У випадку, коли вагу  ,
,  беруть довільно, цей спосіб є кращим, ніж перший, тільки тому, що суперкритерій не перетворюється на нескінченність. Прихильники цього способу посилаються на те, що людина, приймаючи компромісне рішення, подумки зважує всі “за” і “проти”, приписуючи більшу вагу найважливішим для неї факторам. Однак треба мати на увазі, що вагові коефіцієнти не є сталими й можуть змінюватися залежно від ситуації.
беруть довільно, цей спосіб є кращим, ніж перший, тільки тому, що суперкритерій не перетворюється на нескінченність. Прихильники цього способу посилаються на те, що людина, приймаючи компромісне рішення, подумки зважує всі “за” і “проти”, приписуючи більшу вагу найважливішим для неї факторам. Однак треба мати на увазі, що вагові коефіцієнти не є сталими й можуть змінюватися залежно від ситуації.
Приклад 2. Нехай деяка людина виходить із будинку, щоб їхати на роботу. Вона боїться спізнитися і вирішує, яким транспортом скористатися. Трамвай ходить часто, але рухається повільно, автобус – рідше, але –швидше. Можна взяти таксі, але це дорого. Є ще одне рішення – частину шляху проїхати на метро, а потім узяти таксі. Але таксі може не бути, а, добираючись до роботи зі станції метро пішки, вона ризикує спізнитися більше, ніж якби їхала автобусом. Що робити?
Подамо цю задачу як задачу прийняття рішень з двома критеріями: Т (середній очікуваний час запізнення) і S (очікувана вартість проїзду), причому
 .
.
Ці дві вимоги несумісні, тому людина повинна прийняти компромісне, прийнятне за двома критеріями рішення, тобто, підсвідомо зважуючи всі “за” і “проти”, скористатися суперкритерієм вигляду:
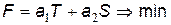 .
.
Аналізуючи цю ситуацію, важливо зрозуміти, що коефіцієнти а1 і а2 –несталі. Вони залежать не тільки від величин Т і S, але й від деяких обставин. Так, якщо людина недавно дістала догану за запізнення, то коефіцієнт при Т, імовірно, збільшиться, а на другий день після зарплати, імовірно, зменшиться коефіцієнт при S. Якщо взяти значення ваги а1 і а2 довільно, то довільним буде “оптимальний” розв’язок.
Із аналізу таких ситуацій видно, що важливим моментом використання будь-якого агрегату є можливість його застосування, не використовуючи інших систем цінностей. Якщо це неможливо, то слід повернутися до конфігуратора, додати до нього моральні, екологічні й інші критерії, а не тільки фінансові.
Одним з найважливіших прикладів агрегування є статистичний аналіз. Статистики – функції вибіркових значень, що вилучають всю корисну інформацію про необхідний параметр із сукупності спостережень.
Статистики використовують таку важливу властивість: за певних умов випадкові величини починають поводитися майже як невипадкові, що дає можливість впевнено оперувати ними і пророкувати результати масових випадкових явищ майже з повною визначеністю.
Це правило має місце за умови, що вплив на суму окремих доданків має бути рівномірно малим, тобто щоб до складу суми не входили члени, які явно переважають за своїм впливом на розсіювання над сукупністю інших.
Мають місце також такі правила.
Правило 1. При досить великій кількості незалежних дослідів середнє арифметичне спостережених значень випадкової величини збігається за ймовірністю з її математичним сподіванням.
Правило 2. Якщо досліджувану випадкову величину можна подати у вигляді суми досить великої кількості незалежних (або слабо залежних) елементарних доданків, кожний з яких окремо порівняно мало впливає на суму, то закон розподілу суми стає приблизно нормальним. Це правило називають центральною граничною теоремою.
| Приклад | Зазначимо, що нормальний закон розподілу відіграє важливу роль у теорії стрільби, є домінуючим (донедавна вважався єдиним і універсальним) у теорії помилок вимірів, залишається найпоширенішим і найважливішим для практики законом помилок і т.д. |
На практиці здійснюється наближена заміна одних законів розподілу іншими: при порівняно малій точності розрахунків така заміна є допустимою. Коли кількість доданків дорівнює десяти (а часто й менше), закон розподілу суми зазвичай замінюється на нормальний.
Висновок із правила 2. Нехай  – незалежні випадкові величини з математичними очікуваннями
– незалежні випадкові величини з математичними очікуваннями  і дисперсіями
і дисперсіями  . Припустимо, що умови центральної граничної теореми виконуються, кількість доданків
. Припустимо, що умови центральної граничної теореми виконуються, кількість доданків  є достатньою для того, щоб закон розподілу величини
є достатньою для того, щоб закон розподілу величини

можна було вважати приблизно нормальним.
Тоді ймовірність того, що випадкова величина  знаходиться у межах ділянки
знаходиться у межах ділянки  , виражається формулою
, виражається формулою
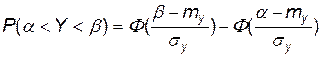 , (3)
, (3)
де  ,
, 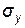 – математичне сподівання й середньоквадратичне відхилення величини
– математичне сподівання й середньоквадратичне відхилення величини  ;
;  – нормальна функція розподілу (таблична функція).
– нормальна функція розподілу (таблична функція).
Зазначимо, що створення агрегату-оператора пов'язано з такими ризиками:
- втрата корисної інформації, тому що агрегування є неминучим перетворенням (наприклад, за сумою не можна відновити доданки), що в загальному випадку призводить до втрат;
- агрегування являє собою вибір певної моделі системи, з яким пов'язані непрості проблеми адекватності;
- деяким агрегатам-операторам властива внутрішня суперечливість, пов’язана з негативними (стосовно цілей агрегування) наслідками.
Дата добавления: 2015-01-01; просмотров: 337; Мы поможем в написании вашей работы!; Нарушение авторских прав |