Агрегат-структура

Важливою, а на етапі синтезу – найважливішою формою агрегування є утворення структур. Під час синтезу структуру майбутньої системи визначають за допомогою агрегату-структури – моделі системи, обумовленої потрійною сукупністю: об'єкта, мети й засобів (у тому числі середовища) моделювання. Найповнішою моделлю є структурна схема, для побудови якої слід пройти етапи моделювання за допомогою “чорного ящика”, моделі складу та моделі структури. Саме об’єднання цих моделей дає можливість синтезувати структурну схему.

Тут важливо пам’ятати, що структуру системи слід задавати у всіх її істотних відношеннях, тому що в інших відношеннях структури утворяться стихійно. Істотні відношення визначаються конфігуратором системи, тому проект будь-якої системи повинен містити розробку стількох структур, скільки мов включено в її конфігуратор. Підкреслимо, що, хоча структури можуть відрізнятися топологічно, вони з різних боків описують ту саму систему, а отже, зв'язані між собою.

Пояснимо випадок агрегування (створення структурної схеми системи) за допомогою агрегату-структури на прикладі побудови структури логічних пристроїв.

Теоретичною основою побудови найпростіших логічних пристроїв є булева алгебра. Відповідно до стандарту ISO 2382/2-76 кожна залежність, що реалізує мету (алгоритм) роботи логічного пристрою, має вигляд

, , (4)

де – і-й вхід; – кількість входів у пристрої; – j-й вихід; – кількість виходів у пристрої.

Залежність (4) – модель “чорнго ящика” – є булевою функцією, у якій кількість можливих станів кожної її незалежної змінної дорівнює двом, а її аргументи визначено на множині . Отже, кількість можливих функцій Y від x аргументів виражається залежністю

.

В алгебрі логіки використовуються логічні операції І, АБО, НЕ – елементи моделі складу, які відбивають алгоритми перетворення інформації, поданої у двійковій системі числення (табл.2). Поняття двійкової змінної та логічної операцій утворюють систему аксіом алгебри логіки .

Коли елементи системи підібрано, модель “чорного ящика” зручно подавати у вигляді таблиці істинності, що визначає значення вихідної функції залежно від комбінації вхідних сигналів (див. табл.2) – зв’язки елементів.

Таблиця .2

Елементи моделі складу та зв’язки у моделі структури

Модель складу	Залежність входу й виходу у моделі структури
Інверсія – логічне заперечення (сполучник НЕ)	Таблиця істинності для логічного елемента НЕ
Диз'юнкція – логічне додавання (сполучник АБО)	Таблиця істинності для логічного елемента АБО
Кон'юнкція – логічне множення (сполучник І)	Таблиця істинності для логічного елемента І

Отже, такий підхід установлює основні закони формування й перетворення логічних функцій і дає можливість подати будь-яку складну функцію у вигляді композиції найпростіших функцій (рис.1), що найчастіше застосовується на практиці, тому що рідко використовуються логічні елементи, які реалізують тільки одну логічну операцію.

а	б
Рис. 1. Композиція складних логічних функцій: а – І-НІ (операція Пірса); б – АБО-НІ (операція Шеффера)

Під час побудови моделі структурної схеми дотримуються такої послідовності дій:

1. Словесно описують роботу схеми – формують конфігуратор системи.

2. Словесний опис формалізують (визначають модель структури) і записують залежно від моделі складу в диз'юнктивній або кон’юнктивній формі за таблицями істинності.

3. Будують структурну схему пристрою.

4. Перевіряють працездатність отриманої моделі (схеми).

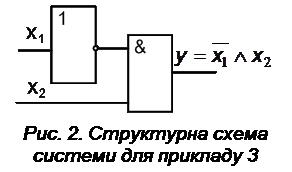
Приклад 3.Робота системи відповідає моделі . Синтезувати структурну схему системи. Якщо на входи цієї системи подано логічні нулі, визначити значення логічної функції на виході.

Аналізуючи модель системи, як її найпростіші елементи виберемо логічні елементи І та НЕ. Структурну схему пристрою наведено на рис.2.

Якщо на вхід цієї системи подано логічний нуль, то відповідно до таблиці істинності логічного елемента НЕ на виході буде логічна одиниця. Якщо на вході елемента сигнали відповідають логічним величинам 1 та 0, то згідно з таблицею істинності логічного елемента І на виході цієї системи буде логічний нуль.

Приклад 4. За допомогою агрегату-структури синтезувати структурну схему логічного пристрою – шифратора.

Відповідно до конфігуратора шифратор – це логічній пристрій, який перетворює позиційний код на двійковий.

Згідно із (6) логічні залежності шифратора запишемо як

;

; (7)

.

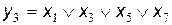Аналізуючи вирази (7), як простіший елемент виберемо логічний елемент АБО, а таблицю істинності, що однозначно описує зв'язки між входами й виходами шифратора, наведено в табл. 3.

Таблиця 3

Таблиця істинності шифратора

Входи	Виходи

Отже, об’єднуючи всі наведені вище моделі, агрегуємо структурну схему шифратора (рис.3).

Рис.3. Структурна схема шифратора

Зазначимо, що існують реальні системи, структуру яких сучасна теорія охопити не в змозі. Під час дослідження цих систем виявляють існування маловивчених способів агрегування, зокрема самоорганізації.

Таким чином, сформулюємо фундаментальні положення та евристичні принципи агрегування систем:

- несуперечність: неможлива одночасна істинність висловлення (А) і суперечного йому висловлення (не А);

- закон достатньої підстави: “... жодне явище не може виявитися істинним або дійсним, жодне твердження – справедливим без достатнього обґрунтування, чому справа стоїть саме так, а не інакше...” (Г.В. Лейбніц);

- закон збереження речовини: речовина нікуди не зникає і нівідкіля не виникає, вона тільки переходить з одного стану в інший;

- властивість симетрії: якщо деякий стан (процес) є у природі, то для нього існує зворотний в часі стан (процес), що також може реалізовуватися в природі;

- принцип простоти: “не слід створювати суті понад необхідності” (У. Оккам);

- принцип “ліні”: кожна людина, що розмовляє, прагне повідомити якнайменше інформації, кожна людина, що слухає, – одержати її якнайбільше, щоб самому менше вдумуватися в зміст висловлення;

- принцип естетики: “фізичний закон має бути математично витонченим” (П. Дірак);

- принцип відповідності: якщо коректно уточнити адекватну модель або область дії адекватної моделі, то можна отримати адекватну модель.