
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показатели безотказности невосстанавливаемых систем
PRINT y$ Результат: “еинаминВ“
Здесь в переменной y$ формируется нужный результат.
Задача 7.1. Напечатать число X (в диапазоне 0-99) прописью. Такая потребность возникает при печати в финансовых документах “суммы прописью”. Результат поместить в переменную P$.
Нам понадобятся три текстовых массива. s1$(0 to 9) для числительных в диапазоне "ноль" – "девять", s2$(10 to 19) для "десять" – "девятнадцать", s3$(2 to 9) для "двадцать" – "девяносто". Начальный и конечный индексы массивов лучше выбирать в соответствии со значениями числительных. Наполнение массивов проще произвести операторами Data и Read.
CLS 'Программа к задаче 7.1
DIM s1$(0 TO 9), s2$(10 TO 19), s3$(2 TO 9)
DATA "ноль","один","два", "три","четыре","пять","шесть","семь","восемь","девять"
READ s1$(0), s1$(1), s1$(2), s1$(3), s1$(4), s1$(5), s1$(6), s1$(7), s1$(8), s1$(9)
DATA "десять","одиннадцать","двенадцать","тринадцать","четырнадцать","пятнадцать",
"шестнадцать","семнадцать","восемнадцать","девятнадцать"
READ s2$(10),s2$(11),s2$(12), s2$(13), s2$(14), s2$(15), s2$(16), s2$(17), s2$(18), s2$(19)
DATA "двадцать","тридцать","сорок","пятдесят","шестьдесят","семдесят","восемдесят","девяносто"
READ s3$(2), s3$(3), s3$(4), s3$(5), s3$(6), s3$(7), s3$(8), s3$(9)
INPUT "введите число X"; x
IF x > 99 THEN PRINT "если число X слишком велико – выход": END
x$ = LTRIM$(STR$(x)) 'число X превращается в сроку X$ с удалением пробелов
IF x < 10 THEN P$= s1$(x): PRINT P$: END 'формирование строки если X < 9
IF x < 20 THEN P$= s2$(x): PRINT P$: END 'формирование строки если X от 10 до 19
'если число от 20
n1 = VAL(MID$(x$, 1, 1)) 'формируются десятки X
n2 = VAL(MID$(x$, 2, 1)) 'формируются единицы X
P$= s3$(n1) + " " + s1$(n2) 'формируется итоговая строка
PRINT P$
@ Задачи для самостоятельного решения.
1). В символьной строке X (придумайте ее сами) удалить лишние (начальные, конечные и сдвоенные) пробелы.
2). В X подсчитать число вхождений слова ‘его’.
3). В X поменять порядок символов внутри каждого слова на обратный.
4). В X напечатать самое длинное слово.
5). В X подсчитать число вхождений произвольного символа.
6). В X подсчитать число вхождений всех встречающихся знаков.
7). В X в каждом слове поменять порядок символов на обратный.
8). В X расположить слова в порядке увеличения их длины.
9). Имеется строка X длиной ≤N, предназначенная для вывода. Выровнять при печати X к правой границе так, чтобы строка занимала все N позиций. Выравнивание производить за счет равномерного увеличения числа пробелов между словами.
10). Зашифровать строку X, заменив каждый символ, на символ, следующий за данным по алфавиту (буква А заменяется на Б и т.д., буква Я заменяется на А). Расшифровать полученный текст.
11). В строке X имеются открывающиеся и закрывающиеся скобки (включая вложенные). Выяснить, правильно ли они расставлены. Если есть ошибки – сообщить об этом конкретно, включая номер позиции, где она обнаружена.
12). Строка X содержит любые русские и латинские символы (как заглавные, так и строчные), цифры и знаки препинания. Преобразовать все символы X в строчные. Результат занести в Y.
13). Пусть имеется таблица работников бригады со столбцами: Имя, Отработано дней, Зарплата. Отсортировать любым методом таблицу по алфавиту. Для упрощения будем считать, что имена не превышают 8-ми символов, содержат только заглавные буквы и не имеют буквы Ё (эта буква в кодовой таблице русских символов находится не на месте).
14). Отсортировать таблицу по алфавиту, где для имен допускаются любые буквы русского алфавита, включая Ё и ё. Сложность здесь заключается как раз в этих буквах. Их коды 240 и 241, т.е. самые большие среди русских букв, в виду чего сравнивать слова придется не целиком, а побуквенно. В случае, если встретилась буква Ё и ё, в программе они должны считаться большими букв Е/е и меньшими Ж/ж.
15). Написать программу, которая из заданной даты (в диапазоне 1900..2100) формирует следующую. Исходная дата задается в форме текстовой строки вида ‘дд.мм.гггг’, например ’06.04.2002’. Подсказка: признаком високосного года является кратность года числу 4. Исключением являются года с двумя нулями на конце, число сотен в которых не кратно 4 (например, 1800, 1900, 2100).
16). Написать программу, которая от заданной даты (диапазон 1900¸2100) находит новую, отстоящую от данной на М месяцев. Если в новом месяце такой даты нет, берется последний день нового месяца. Так, если вследствие вычислений получилась, например, дата 31 сентября, в качестве результата нужно взять 30 сентября.
17). Написать программу, которая от заданной даты (1900¸2100), находит новую, отстоящую от данной на X дней.
18). Преобразовать число X, отображенное цифрами, в число “прописью”, что необходимо для финансовых документов:
а). X имеет три разряда в диапазоне 0¸999.
б). X имеет шесть разрядов в диапазоне 0¸999 999.
в). X имеет девять разрядов в диапазоне 0¸999 999 999.
Результатом преобразования, например числа 23 245 012, должно быть выражение “двадцать три млн. двести сорок пять тыс. двенадцать руб.” Основой для решения этих задач является задача 7.1, разобранная выше. Понадобится еще массив для сотен числительных “сто” ¸ “девятьсот”, и массив для разряда единиц тысяч, поскольку “одна” тысяча, но “один” рубль. При формировании строки следует разбить исходное число на триады (т.е. по три разряда), для которых техника преобразования практически аналогична.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Составить блок-схемы и программы решения пяти задач контрольной работы. Всего вариантов 25 (от 0 до 24). Вариант определяются числом, образованным из двух последних цифр шифра студента, следующим образом. Если число находится в диапазоне 0¸24, – это и будет нужный вариант. Если оно больше, то из него нужно отнимать число 25 до тех пор, пока не будет получено число менее 25. Так, для шифра 0469, необходимо выполнить 19-ый вариант (69-25-25=19).
ЗАДАЧА 1.Имеется четыре A,B,C,D произвольных числа. ЭВМ должна ответить на вопрос: Правда ли что ...? (вопрос найдете в таблице вариантов). Ответ ЭВМ должна вывести в виде текста – слов ”Правда” или ”Неправда”.
| все числа отрицательны? | все числа положительны? | ||
| среди чисел есть четные? | точно два из чисел равны? | ||
| не все числа отрицательны? | не все числа положительны? | ||
| среди чисел есть нечетные? | числа расположены в порядке убывания? | ||
| хотя бы два из чисел равны? | все числа равны между собой? | ||
| среди этих чисел нет равных? | среди этих чисел есть равные? | ||
| все числа больше 0 и меньше 7? | первое число меньше остальных? | ||
| среди чисел есть кратные трем? | среди чисел нет отрицательных? | ||
| первое число не самое маленькое? | среди чисел точно одно больше 6? | ||
| среди чисел есть кратные трем? | ни одно число не превышает 9? | ||
| последнее число не самое маленькое? | среди чисел точно одно <0? | ||
| точно два из чисел не равны между собой? | имеется хотя бы одно число, кратное пяти? | ||
| каждое из первых двух чисел больше каждого из последних двух? |
ЗАДАЧА 2.Составить программу вычисления и выдачи на печать суммы (или произведения) N элементов бесконечного числового ряда. Здесь и далее следует пользоваться операторами цикла FOR или WHILE.
| y=1-6+11-16+21-... | y=256(-64)16(-4)1... | y=32(-16)8(-4)2… | y=4(-6)8(-10)12… | y=85-80+75-70+... | |||||
| y=-2+5-8+11-14+... | y=50-40+30-20+10-... | y=(-1)4(-16)64... | y=(-512)256(-128)... | y=-243+81-27+9-... | |||||
| y=-4+8-16+32-64+... | y=3-9+27-81+243... | y=1(-3)9(-27)81... | y=(-64)32(-16)8(-4)… | y=-20+18-16+14-... | |||||
| y=2-6+18-54+162-... | y=70-65+60-55+50-... | y=16(-8)4(-2)1… | y=1000(-100)10(-1)... | y=42-40+38-36+... | |||||
| y=60-57+54-51+48-... | y=125(-25)5(-1)0,2... | y=60-55+50-45+... | y=48(-24)12(-6)3... | y=3-5+7-9+11-... |
ЗАДАЧА 3.Имеется массив A из N произвольных чисел A(N), среди которых есть положительные, отрицательные и равные нулю. Составить программу, выполняющую задачу в соответствии с вариантом.
| Вычислить сумму всех четных положительных чисел. Например, если A={2,4,–3,0,5,1,6}, результат: 2+4+6=12. | |
| Вычислить количество чисел, квадрат которых меньше 10. Так, при A={2,4,–3,3,5,2,1}, результат: 5 (числа 2,-3,3, 2,1). | |
| Вычислить количество положительных и нулевых чисел и сумму отрицательных. Например, если A={2,4,–3,3,5,–2,1}, результат: положительных чисел 5 (2,4,3,5,1), нулевых – 0 (нет), сумма отрицательных –5 (–3+–2=–5). | |
| Ответить на вопрос: правда ли что среди чисел имеются отрицательные (ответ должен быть в виде слов “ДА” или “НЕТ”). Например, если A={2,4,–3,3,5,–2,1}, результат: ДА (–3, –2). | |
| Напечатать все числа из очереди, квадрат которых превышает 7, но меньше 50. Например, если A={2,4,–3,3,5,–2,8}, результат: числа 4, –3, 3, 5. | |
| Вычислить произведение всех положительных чисел меньших 20. Так, если A={2,24,-3,6,5,-2,33}, результат: 2×6×5=60. | |
| Суммировать числа до тех пор, пока не встретится число 2. Напечатать получившуюся сумму. Если двойка не встретилась, напечатать текст “Двойки нет”. Например, если A={7,4,–3,2,5,–2,1}, результат: 7+4–3=8. | |
| Выяснить, каким по счету в очереди стоит число 3. Если троек несколько, нас интересует только первая из них. Если троек нет совсем, напечатать сообщение “Троек нет”. Например, если A={2,4,–3,3,5,–2,1}, результат: 4. | |
| Подсчитать количество положительных и отрицательных чисел и количество нулей. Например, если A={2,4,–3,0,5,–2,5}, результат: 4; 2; 1. | |
| Напечатать те числа из массива, которые образуют убывающие последовательности. Например, если A={2,4,3,0,2,5,–2,5}, результат: 4, 3, 0 и 5, –2. | |
| Найти сумму и количество всех нечетных положительных чисел. Так, если A={9,4,–3,0,5,1,–7}, результат: сумма =9+5+1=15, количество =3. | |
| Найти максимальное и минимальное числа. Напечатать те элементы массива, которые в массиве находятся между ними. Так, если A={2,4,–3,0,2,5,–2}, результат: –3,0,2,5 (max=5, min=–3). | |
| Найти номер последнего положительного элемента в массиве. Например, если A={2,4,–3,0,2,5,–2}, результат: 6 (последнее число 5). | |
| Найти номера первых двух рядом стоящих одинаковых элементов в массиве. Так, если A={2,6,4,4,2,5,5,4}, результат: 3 и 4 (равные значения 4 и 4). | |
| Выяснить, есть ли одинаковые элементы в массиве. Ответ ДА/НЕТ. Так, если A={2,4,3,0,2,5,4}, результат: ДА (одинаковые значения 2 и 2). | |
| Найти максимальный четный элемент в массиве из всех положительных элементов. Так, для A={2,4,–3,6,2,9,–2}, результат: 6. | |
| Найти произведение четных элементов, находящихся в диапазоне от 3 до 13. Например, если A={2,4,5,2,6,–2,20,8}, результат: 4×6×8. | |
| Найти максимальное и минимальное нечетные числа и их среднее арифметическое. Так, если A={8,4,–2,6,2, 7, –5}, результат: 7 и –5 и (7–5)/2=1. | |
| Найти сумму элементов кратных трем. Например, если A={2,4,9,2,6,–12,0}, результат: 9+6–12=3. | |
| Найти номер максимального четного элемента в массиве. Например, если A={2,4,–3,6,2,9,–2}, результат: 4. | |
| Напечатать номера элементов кратных одновременно двум и трем. Так, если A={3,6,9,2,12, 2,24}, результат: 6,12,24. | |
| Напечатать произведение элементов следующих за минимальным числом. Так, при A={3,4,9,2,–5,2,3}, результат: 2×3. | |
| Найти произведение элементов кратных трем. Например, если A={2,4,9,2,6,–3,0}, результат: 9×6× (–3)=–162. | |
| Напечатать в обратном порядке все положительные элементы. Так, если A={2,4,–9,5,6,–3,2}, результат: 2,6,5,4,2. | |
| Напечатать сумму элементов предшествующих минимальному числу. Так, если A={3,4,9,2,–5, 2,3}, результат: 3+4+9+2=18. |
ЗАДАЧА 4.Составить программу вычисления числового ряда для известного числа членов ряда N. Перед программированием следует выявить и написать аналитические соотношения, описывающие все имеющиеся зависимости.
| Y=(7+35/1)(8-3-4/2)(9+33/3)(10+3-2/3)... | Y=(2+1/81)-(4-2/27)+(8+4/9)-(16-8/3)+ | ||
| Y=(1+2-1/2)(-2+22/3)(3+2-3/4)(-3+24/4)... | Y=(8+35)-(4+3-4)+(2+33)-(1+3-2)+... | ||
| Y=(1/24+1)(2/23-2)(3/22+4)(3/21-8)... | Y=(7+35/1)(8-3-4/2)(9+33/3)(10+3-2/4)... | ||
| Y=(33-1)(3-2+2)(31-4)(3-0+8)... | Y=(2-1/2)(22/-5)(2-4/8)(28/-11)... | ||
| Y=-8/(25-2)Ÿ4/(24+4)Ÿ-2/(23-5)Ÿ1/(21+6)... | Y=(3-1/2)(42/-5)(5-3/8)(64/-11)... | ||
| Y=(2/16+8)(2/8-10)(2/4+12)(2/2-14)... | Y=(1+24-8)(2-2-3-4)(4+22-2)(8+2-1-1)... | ||
| Y=(1+2-1/2)(3+22/3)(5+2-3/4)(7+24/5)... | Y=(7+2/2)-(6-3/4)+(5+4/8)-(4-5/16)+... | ||
| Y=(2-4-8+1)(23-4+3)(2-2-2+5)(21+1+7)... | Y=(1-2/5)+(2+4/10)+(3-8/15)+(4+16/20)... | ||
| Y=-(3/16+1)+(3/8-2)-(3/4+3)+(3/2-4)... | Y=(2-1/27+4)(22/9-8)(2-3/3+16)(24/1-32)... | ||
| Y=(3+1-1/81)(5-2+1/27)(7+3-1/9)(9-4+1/3)... | Y=(1+25/1)(10+2-4/2)(100+23/3)... | ||
| Y=(2-1/81)(4+1/27)(8-1/9)(16+1/3)... | Y= -1/(18+2)Ÿ2/(2-4+4)Ÿ-3/(32+6)... | ||
| Y=28/(3-16)Ÿ2-4/(4+8)Ÿ22/(5-4)... | Y=(0-2/5)+(2+3/10)+(4-4/15)+(6+5/20)... | ||
| Y=(4/2+8)(5/6-9)(6/18+10)(7/54-11)... |
Указания к решению задачи.Пусть: Y= 2-1Ÿ22Ÿ 2-3Ÿ 24
-5+16 5-8 -5+4 5-2
 Сначала необходимо выписать все, наблюдаемые в ряду, соотношения. Для этого введем переменные. Степень двойки обозначим буквой A, знак при ней и знак при числе 5 буквой Z (так как они совпадают), второе слагаемое в знаменателе 16 – буквой В, а знак при нем -Z (этот знак противоположен остальным). Формула справа.
Сначала необходимо выписать все, наблюдаемые в ряду, соотношения. Для этого введем переменные. Степень двойки обозначим буквой A, знак при ней и знак при числе 5 буквой Z (так как они совпадают), второе слагаемое в знаменателе 16 – буквой В, а знак при нем -Z (этот знак противоположен остальным). Формула справа.
Алгоритм решения (для заданного числа членов N):
1. Ввести значение N.
2. Задать исходные значения переменных (Y=1, Z=–1, A=1, B=16)
3. Вычислить очередное значение Y.
4. Вычислить новые значения A, В, Z.
5. Вернуться к пункту 3, если число выполненных циклов £N, иначе, завершение цикла и печать Y.
 Y =Y(2ZA/(ZŸ5–ZŸB)) Y = 1
Y =Y(2ZA/(ZŸ5–ZŸB)) Y = 1
Z = –Z Z = –1
A = A+1 A = 1
B = –B/2 B = 16
ЗАДАЧА 5.Выполнить действия над массивами. В таблице при формулировании задания для разъяснения его сути справа отображены примеры исходных X и результирующих Y массивов с конкретными числами. Программа, естественно, должна обрабатывать любые числа для массивов произвольной размерности N. Программа должна предъявлять исходные и новые (если требуется) массивы.
| Заполнить Y таким образом, чтобы в его начале оказался первый элемент X, затем в его конце – второй, затем в начале – третий, в конце – четвертый и т.д. | X | |||||||
| Y | ||||||||
| Переписать все элементы X для 3<X(i)<10 в начало Y, подсчитать их количество и среднее арифметическое. В примере таких чисел 3. Среднее 18/3=6. | X | |||||||
| Y | ||||||||
| Найти максимальный и минимальный элементы X и поменять их местами в массиве Y. В примере Xmax=8, Xmin=1. | X | |||||||
| Y | ||||||||
| Взять из X и расположить в массиве Y сначала все положительные, а затем отрицательные элементы. | -3 | -4 | -1 | X | ||||
| -3 | -4 | -1 | Y | |||||
| Изменить порядок элементов массива X на обратный и заполнить ими массив Y. | X | |||||||
| Y | ||||||||
| Занести из X в Y сначала элементы, находившиеся на четных местах в X, а затем – на нечетных. | X | |||||||
| Y | ||||||||
| Заполнить Y нарастающими суммами элементов X. | -2 | X | ||||||
| Y | ||||||||
| Найти максимальный элемент X и заполнить им Y. | X | |||||||
| Y | ||||||||
| Заполнить массив Y четными элементами массива X. | X | |||||||
| Y | ||||||||
| Заполнить массив Y нарастающими произведениями элементов массива X. | X | |||||||
| Y | ||||||||
| Заполнить Y нечетными элементами массива X. | X | |||||||
| Y | ||||||||
| Сдвинуть вправо на две позиции содержимое X и заполнить им массив Y. | X | |||||||
| Y | ||||||||
| Сдвинуть влево на две позиции содержимое X и заполнить им массив Y. | X | |||||||
| Y | ||||||||
| Взять из X и расположить в массиве Y сначала все, отрицательные, а затем положительные элементы. | -3 | -4 | -1 | X | ||||
| -3 | -4 | -1 | Y | |||||
| Напечатать все элементы, которые встречаются более одного раза. В примере это 5 и 3. | X | |||||||
| Напечатать все элементы, которые не повторяются. Здесь это 2 и 4. | X | |||||||
| Скопировать в Y те элементы массива X, которые делятся на 3 без остатка. | -8 | -3 | X | |||||
| -3 | Y | |||||||
| Заполнить массив Y произведениями соседних двух элементов X. | -2 | X | ||||||
| -8 | Y | |||||||
| Заполнить массив Y произведениями соседних трех элементов X. | X | |||||||
| Y | ||||||||
| Заполнить Y элементами X, находящимися между его максимальным и минимальным значениями. | X | |||||||
| Y | ||||||||
| Заполнить массив Y номерами всех четных элементов массива X. | X | |||||||
| Y | ||||||||
| Заполнить массив Y элементами массива X, находящимися прежде его максимального значения в X. | X | |||||||
| Y | ||||||||
| Заполнить массив Y элементами массива X, находящимися после его максимального значения в X. | X | |||||||
| Y | ||||||||
| Поменять местами соседние элементы массива X и заполнить ими массив Y. | X | |||||||
| Y | ||||||||
| Изменить порядок элементов левой и правой половин массива X на обратный и заполнить ими массив Y. | X | |||||||
| Y |
Глава 1. Основные понятия и показатели надежности экономических информационных систем
Основные понятия и определения
В настоящее время в теории надежности существует единая установившаяся терминология, которая охватывает важнейшие понятия и определения. Основные понятия теории надежности изложены в ряде стандартов [23 - 28]. Надежность системы является одной из основных составляющих его качества. Дадим определения понятиям согласно ГОСТа по надежности. Качество - совокупность свойств продукции, которая позволяет оценить пригодность продукции удовлетворять определенным потребностям в соответствии с её назначением (рис 1.1).

Рис. 1.1. Структура свойств качества и надежности
Одним из качеств изделия является надежность - особое свойство, которое позволяет определить стабильность всех других свойств качества изделия во времени.
Свойство - объективная особенность изделия, которое проявляется при его создании, эксплуатации и потреблении. Надежность системы (согласно ГОСТа 27.002-89) - свойство системы выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки. Исправное состояние - состояние, при котором система обладает полным набором свойств и выполняет все заданные функции с параметрами, установленными в технической документации.
Работоспособность - состояние, при котором система выполняет все заданные функции с параметрами, установленными требованиями технической документации, но с отсутствием некоторых несущественных для нормального функционирования свойств. Отказ - событие, которое заключается в нарушении работоспособности. Следует отметить, что под отказом надо понимать не только полное нарушение работоспособности, но и выход параметров изделия за границы, установленные требованиями технической документации. Значит, после отказа система либо полностью прекращает свою работу, либо продолжает функционировать с пониженным качеством. Во многих случаях понятие отказа удобно подразделять на его виды в соответствии с классификационными признаками:
1. По характеру возникновения:
- Внезапные (катастрофические). Возникают в результате резкого (скачкообразного) изменения выходных показателей системы;
- Постепенные (параметрические). Образуются при постепенном снижении выходных параметров системы во времени и когда эти параметры пересекают критическое значение, считается, что отказ произошел.
2. По степени очевидности:
- Явные (очевидные). Явные отказы системы обнаруживаются при внешнем осмотре или включении системы;
- Скрытые (неочевидные). Выявляются инструментальными средствами.
3. По связи с отказами других элементов:
- Зависимые (вторичные отказы). Возникают под влиянием отказов других элементов;
- Независимые (первичные отказы).
4. По времени существования:
- Устойчивые (окончательные). Устраняются только в результате ремонта;
- Перемежающие отказы (самопроизвольно возникают и устраняются). Исчезают без вмешательства обслуживающего персонала (например, сбои ЭВМ).
5. По влиянию на ремонтопригодность:
- Неисправности. Устраняются путем мелкого ремонта;
- Аварии. Требуют длительного восстановления и больших ремонтных работ.
6. По природе возникновения:
- Физические. Проявляются в физическом нарушении работоспособности;
- Функциональные. Теряют способность системы выполнять некоторые или все функции (например, при отсутствии физического отказа ЭВМ может неправильно выполнять логические операции).
Надежность является комплексным свойством системы и включает в себя еще четыре других свойства (рис 1.2):
1. Безотказность.
2. Долговечность.
3. Ремонтопригодность.
4. Сохраняемость.
1. Безотказность - свойство системы не утрачивать работоспособность в течение заданной наработки без перерывов.
2. Долговечность - свойство системы сохранять работоспособность до предельного состояния (до списания) с перерывами на техническое обслуживание и ремонт.
3. Ремонтопригодность - свойство системы обнаруживать, устранять и предупреждать неисправность и отказы путем проведения технического обслуживания и ремонта.
4. Сохраняемость - свойство системы сберегать свои эксплуатационные показатели в течение и после срока транспортирования или хранения на складе.

Рис. 1.2. Понятийная схема свойств надежности
Все системы подразделяются на восстанавливаемые и невосстанавливаемые. Невосстанавливаемые системы эксплуатируются до первого отказа. У восстанавливаемых систем может быть поток отказов. Кроме того, системы делятся на ремонтируемые и неремонтируемые. Это технические термины, говорящие о возможности ремонта системы. Так как ремонт может быть дорогой или в условиях эксплуатации не возможным, то система может быть ремонтируемой, но относится к классу невосстанавливаемых.
Понятия восстанавливаемых и невосстанавливаемых систем применяются для расчетов их надежности.
В связи с различными этапами жизненного цикла возникают специфические задачи обеспечения надежности ИС и используются соответствующие методы оценки надежности:
1. Этап проектирования. Схемно-конструктивные методы повышения надежности:
- Выбор и обоснование показателя эффективности ИС и определение его взаимосвязи с показателем надежности;
- Нормирование надежности. Определение оптимального уровня показателя надежности системы, которой она должна обладать во время эксплуатации системы;
- Расчет показателя надежности всей системы, если известны показатели надежности всех элементов;
- Решение задачи оптимального резервирования (дублирования отдельных элементов).
2. Этап изготовления. Производственные методы повышения надежности:
- Автоматизация технологических процессов;
- Методы статистического регулирования надежности;
- Тренировка элементов и систем (испытание сложной системы в течение небольшого промежутка времени с тем, чтобы выявить производственные дефекты).
3. Этап эксплуатации. Эксплуатационные методы повышения надежности:
o Использование диагностических систем, которые выявляют скрытые дефекты;
o Прогнозирование отказов системы.
Применение гибкой системы технического обслуживания и ремонта (ремонт производится в зависимости от состояния системы).
1.2. Система показателей надежности
показатели безотказности, сохраняемости,
ремонтопригодности, долговечности
Рассмотрим количественные показатели случайных величин, которые могут характеризовать свойства безотказности, ремонтопригодности, сохраняемости и долговечности. В качестве единиц измерения применяются:
- для безотказности - непрерывное время безотказной работы системы (наработка на отказ T’);
- для долговечности - время от момента изготовления системы до предельного состояния или списания. (срок службы T’’);
- для ремонтнопригодности - время восстановления работоспособности T’’’;
- для сохраняемости - случайное время сохранения работоспособности в состоянии хранения “T”.
Случайные величины, позволяют количественно оценить путем применения математического аппарата теории вероятностей и математической статистики. Полной характеристикой любой случайной величины является закон ее распределения, используемый в двух видах: как функция распределения (интегральный закон) и как плотность распределения (дифференциальный закон).
Функцией распределения называется функция F(t), определяющая вероятность того, что случайная величина Т примет значение, меньшее заданной величины t, т.е.:
 .
.
Плотностью распределения вероятностей непрерывной случайной величины Т в диапазоне от 0 до бесконечности называют функцию f ( t ) - первую производную от функции распределения F ( t ):
 .
.
В теории надежности широко используются еще две функции:
обратная функция распределения:

интенсивность:

Рассмотрим графики этих функций.(рис. 1.3-1.6).

| 
|
Рис.1.3. График функции  Рис.1.4. График функции
Рис.1.4. График функции 

| 
|
Рис. 1.4. График функции  Рис.1.5. График функции
Рис.1.5. График функции 
Зависимость между функциями b(t) и  можно определить из соотношений:
можно определить из соотношений:
 , (1.2.5)
, (1.2.5)
 . (1.2.6)
. (1.2.6)
Подставим выражение (1.2.6) в (1.2.5):
 .
.
Проинтегрируем обе части выражения:

Таким образом, получаем зависимость  от b(t):
от b(t):
 .
.
Показатели безотказности невосстанавливаемых систем
В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t) , которая в данном случае будет называться функцией вероятности отказа Q ( t ), т.е.:
 .
.
Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t:
 .
.
Графики, дающие представление о характерах изменения функций P(t) и Q(t), представлены на рисунке:

Рис.1.6. График изменения функций P(t) и Q(t)
Плотность распределения вероятностей как показатель безотказности невосстанавливаемых систем принимает смысл плотности распределения наработки на отказ fH(t), а интенсивность b(t) принимает смысл функции интенсивности отказов l(t):
 .
.
 .
.
Между функциями P(t) и l(t) существует взаимосвязь:
 .
.
Взаимосвязь между функциями fH(t) и l(t) можно определить из соотношения:
 .
.
Если одна из четырех функций известна, то остальные три можно вычислить по формулам, приведенным в таблице.
Удобный и наглядный физический смысл имеет показатель "средняя наработка на отказ", который равен математическому ожиданию времени исправной работы до первого отказа:
 .
.
Свойства функции безотказной работы P(t):
1.При t=0, P(t)=1 , т.е. в нулевой момент времени система будет работоспособна.
2. P(t) — монотонно убывающая функция во времени.
3.При t→∞, P(t) → 0.
Таблица 1.1. Взаимосвязь показателей безотказности невосстанавливаемых систем
| Определяемый показатель | Заданный показатель | |||
| Q(t) | P(t) | fn(t) | λ  (t) (t)
| |
| Вероятность отказа Q(t) | — | 1 – P(t) | 
| 
|
| Вероятность безотказной работы P(t) | 1 – Q(t) | — |  
|  
|
| Плотность распределения наработки на отказ fn(t) | 
| 
| — | 
|
| Интенсивность отказов l (t) | 
| 
| 
| — |
На практике часто требуется определить показатели безотказности при том условии, что элемент, проработавший время t1, будет безотказно работать в течение промежутка времени от t1 до t2 (t2>t1). В этом случае основные показатели находятся как условные вероятности. Условная вероятность безотказной работы в течение наработки t = t2 - t1 (рис. 1.7) при условии, что система безотказно проработала от 0 до t1, равна:
 .
.

Рис.1.7. График условной вероятности работы системы
Условная вероятность отказа равна:
 .
.
Условная интенсивность отказа равна:
 .
.
Условная наработка на отказ равна:
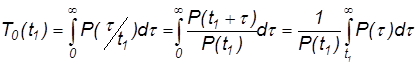 .
.
Теперь перейдем к рассмотрению статистических оценок показателей безотказности, которые в литературе обозначаются либо символом ^ либо *. Пусть на испытания было поставлено No систем, которые с течением времени отказывали, что модно представить временной диаграммой (No - количество изделий, n(t) - количество отказавших изделий за время t):

Рис.1.9. Результаты испытания No систем
Показатели безотказности можно оценивать приближенно по статистическим данным. Рассмотрим формулы для определения статистических значений показателей безотказности. Статистическая оценка вероятности отказа:
 .
.
Статистическая оценка вероятности безотказной работы:
 .
.
Статистическая оценка плотности распределения наработки на отказ:
 .
.
Статистическая оценка интенсивности отказов:

 ,
,
где  .
.
Статистическая оценка средней наработки на отказ находится по формуле:
 ,
,
где ti — наработка на отказ i-й системы.
Дата добавления: 2015-01-01; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |