
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания расчетно-графической работы
Задание 1.
Найти: а) обратную матрицу  . Проверить равенство
. Проверить равенство  ;
;
б) матрицу  , где
, где  получается из
получается из  ее транспонированием
ее транспонированием
| Вариант | Матрица 
| Вариант | Матрица 
|
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 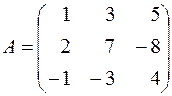
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
Задание 2.Решить системы уравнений по правилу Крамера.
| № варианта | Исходные данные |
 
| |

| |

| |

| |

| |

| |

| |

| |

| |

|
Задание 3.
Решить системы методом Гаусса. Записать общее решение системы и два частных решения.
| Вариант | Система | Вариант | Система |
| 1. | 
| 2. | 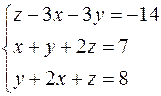
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 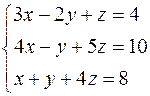
| 8. | 
|
| 9. | 
| 10. | 
|
Задание 4.
Даны координаты вершин треугольника ABC. Найти: длины сторон треугольника ABC; 2) внутренние углы данного треугольника; 3) длину медианы AE; 4) уравнения сторон AB, BC, CA (общее, каноническое, проходящей через две точки, параметрическое, с угловым коэффициентом). Сделать чертеж.
| № варианта | Исходные данные |
| A( 4 ; 0 ), B( 7 ; 4 ), C( 8 ; 2 ) | |
| A( 2 ; 2 ), B( 5 ; 6 ), C( 6 ; 4 ) | |
| A( 0 ; 2 ), B( 3 ; 6 ), C( 4 ; 4 ) | |
| A( 4 ; 1 ), B( 7 ; 5 ), C( 8 ; 3 ) | |
| A( 3 ; 2 ), B( 6 ; 6 ), C( 7 ; 4 ) | |
| A(-2 ; 1 ), B( 1 ; 5 ), C( 2 ; 3 ) | |
| A( 4 ; -3), B( 7 ; 1 ), C( 8 ;-1 ) | |
| A(-2 ; 2 ), B( 1 ; 6 ), C( 2 ; 4 ) | |
| A( 5 ; 0 ), B( 8 ; 4 ), C( 9 ; 2 ) | |
| A( 2 ; 3 ), B( 5 ; 7 ), C( 6 ; 5 ) |
Задание 5.
Найти пределы данных функций:
| вариант | |
| 1. | а)  . б) . б) 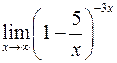
|
| 2. | а)  б) б) 
|
| 3. | а)  б) б) 
|
| 4. | а) 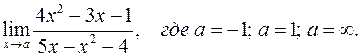 б) б) 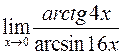
|
| 5. | а) 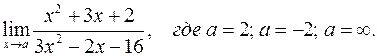 б) б) 
|
| 6. | а)  б) б) 
|
| 7. | а)  б) б) 
|
| 8. | а)  б) б) 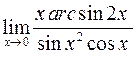
|
| 9. | а)  б) б) 
|
| 10. | а)  б) б) 
|
Задание 6.
Найти производные заданных функций:
| Вариант | Функция 
| |
| 1. | а) 
| б) 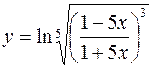
|
в) 
| г) 
| |
| 2. | а) 
| б) 
|
в) 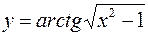
| г) 
| |
| 3. | а) 
| б) 
|
в) 
| г) 
| |
| 4. | а) 
| б) 
|
в) 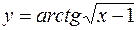
| г) 
| |
| 5. | а) 
| б) 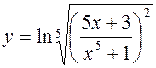
|
в) 
| г) 
| |
| 6. | а) 
| б) 
|
в) 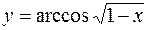
| г) 
| |
| 7. | а) 
| б) 
|
в) 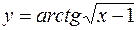
| г) 
| |
| 8. | а) 
| б) 
|
в) 
| г) 
| |
| 9. | а) 
| б) 
|
в) 
| г) 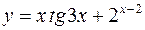
| |
| 10. | а) 
| б) 
|
в) 
| г) 
|
Задание 7.
Исследовать методами дифференциального исчисления функции  и, используя результаты исследования, построить графики данных функций по следующей схеме:
и, используя результаты исследования, построить графики данных функций по следующей схеме:
Ø найти область определения функции;
Ø исследовать на четность, нечетность, периодичность;
Ø найти точки пересечения графика функции с осями координат;
Ø исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в точках разрыва;
Ø найти точки экстремума и интервалы ее монотонности;
Ø найти точки перегиба, интервалы выпуклости и вогнутости графика функции;
Ø найти асимптоты графика, используя результаты предыдущих исследований.
1. а) 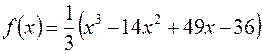 ; б)
; б)  .
.
2. а)  ; б)
; б)  .
.
3. а) 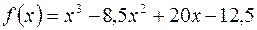 ; б)
; б)  .
.
4. а)  ; б)
; б)  .
.
5. а)  ; б)
; б)  .
.
6. а)  ; б)
; б)  .
.
7. а)  ; б)
; б) 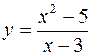 .
.
8. а)  ; б)
; б)  .
.
9. а)  ; б)
; б)  .
.
10. а)  ; б)
; б) 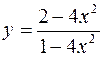
Задание 8.
Вычислить частные производные и полные дифференциалы от заданных функций:
| вариант | |
| 1. | а)  б) б) 
|
| 2. | а)  б) б) 
|
| 3. | а)  б) б) 
|
| 4. | а) 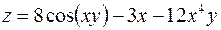 б) б) 
|
| 5. | а) 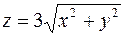  б) б) 
|
| 6. | а)  б) б) 
|
| 7. | а)  б) б) 
|
| 8. | а)   б) б) 
|
| 9. | а)  б) б) 
|
| 10. | а)  б) б) 
|
Задание 9.
Найти экстремумы функций двух переменных:
| вариант | |
| 1. | 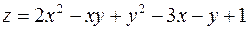
|
| 2. | 
|
| 3. | 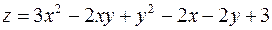
|
| 4. | 
|
| 5. | 
|
| 6. | 
|
| 7. | 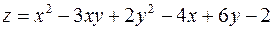
|
| 8. | 
|
| 9. | 
|
| 10. | 
|
Задание 10. Вычислить неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
| вариант | |||
| 1. | а) 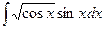 г)
г) 
| б)  д)
д) 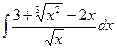
| в)  е)
е) 
|
| 2. | а) 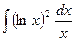 г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 3. | а) 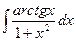 г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 4. | а)  г)
г) 
| б) 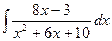 д)
д) 
| в)  е)
е) 
|
| 5. | а) 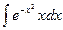 г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 6. | а) 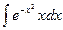 г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 7. | а) 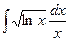 г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 8. | а) 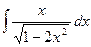 г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 9. | а)  г)
г) 
| б)  д)
д) 
| в)  е)
е) 
|
| 10. | а)  г)
г) 
| б)  д)
д) 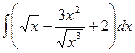
| в)  е)
е) 
|
Задание 11. Вычислить определенные интегралы.
| вариант | ||
| 1. | a) 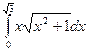
| б) 
|
| 2. | a) 
| б) 
|
| 3. | a) 
| б) 
|
| 4. | a) 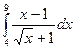
| б) 
|
| 5. | a) 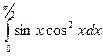
| б) 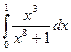
|
| 6. | a) 
| б) 
|
| 7. | a) 
| б) 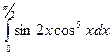
|
| 8. | a) 
| б) 
|
| 9. | a) 
| б) 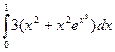
|
| 10. | a) 
| б) 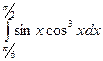
|
Задание 12. Вычислить площадь фигуры, ограниченной заданными кривыми.
| вариант | |||
| 1. | a) 
| б) 
| в) 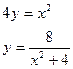
|
| 2. | a) 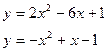
| б) 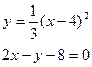
| в) 
|
| 3. | a) 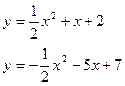
| б) 
| в) 
|
| 4. | a) 
| б) 
| в) 
|
| 5. | a) 
| б) 
| в) 
|
| 6. | a) 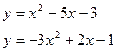
| б) 
| в) 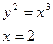
|
| 7. | a) 
| б) 
| в) 
|
| 8. | a) 
| б) 
| в) 
|
| 9. | a) 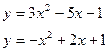
| б) 
| в) 
|
| 10. | a) 
| б) 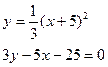
| в) 
|
Задание 13.
Найти общее решение дифференциального уравнения:
| вариант | |
| 1. | 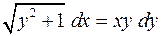
|
| 2. | 
|
| 3. | 
|
| 4. | 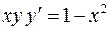
|
| 5. | 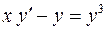
|
| 6. | 
|
| 7. | 
|
| 8. | 
|
| 9. | 
|
| 10. | 
|
Задание 14.
Найти общее решение и частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям:
| вариант | |
| 1. | а)  б)
б) 
|
| 2. | а)  б)
б) 
|
| 3. | а)  б)
б) 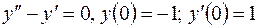
|
| 4. | а)  б)
б) 
|
| 5. | а) 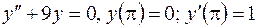 б)
б) 
|
| 6. | а) 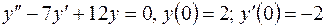 б)
б) 
|
| 7. | а)  б)
б) 
|
| 8. | а) 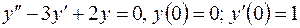 б)
б) 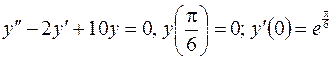
|
| 9. | а)  б)
б) 
|
| 10. | а) 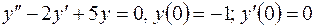 б)
б) 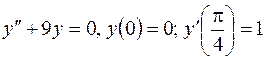
|
Задание 15.Исследовать сходимость числового ряда:
| вариант | |||
| 1. | a) 
| б) 
| в) 
|
| 2. | a) 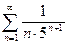
| б) 
| в) 
|
| 3. | a) 
| б) 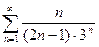
| в) 
|
| 4. | a) 
| б) 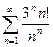
| в) 
|
| 5. | a) 
| б) 
| в) 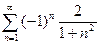
|
| 6. | a) 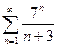
| б) 
| в) 
|
| 7. | a) 
| б) 
| в) 
|
| 8. | a) 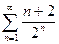
| б) 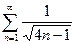
| в) 
|
| 9. | a) 
| б) 
| в) 
|
| 10. | a) 
| б) 
| в) 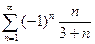
|
Задание 16. Найти радиус, интервал сходимости степенного ряда и провести исследование на концах интервала:
| вариант | ||
| 1. | a) 
| б) 
|
| 2. | a) 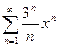
| б) 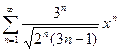
|
| 3. | a) 
| б) 
|
| 4. | a) 
| б) 
|
| 5. | a) 
| б) 
|
| 6. | a) 
| б) 
|
| 7. | a) 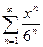
| б) 
|
| 8. | a) 
| б) 
|
| 9. | a) 
| б) 
|
| 10. | a) 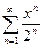
| б) 
|
Дата добавления: 2015-01-01; просмотров: 245; Мы поможем в написании вашей работы!; Нарушение авторских прав |