
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для расчета средней квадратичной скорости выражение (1) удобно преобразовать, умножив числитель и знаменатель на NA.
<uкв>=  ;
;
<uкв>=13,7×102 м/с – для гелия;
<uкв>=5,17×102 м/с – для азота.
Средняя полная энергия молекулы зависит от числа степеней свободы молекулы:
<E0>=  .
.
Полная кинетическая энергия всех молекул, равная для идеального газа его внутренней энергии, может быть найдена как произведение Е0 на число всех молекул:
Е=U=Е0×N; N=  .
.
Гелий – одноатомный газ Þ i=3, тогда <E0>=6,2×10-21 Дж.
Азот – двухатомный газ Þ i=5, тогда <E0>=10,4×10-21 Дж.
Полная энергия всех молекул
Е=  .
.
Для гелия W=93,5×103 Дж; для азота W=22,3×103 Дж.
Ответ: для гелия W=93,5×103 Дж; для азота W=22,3×103 Дж
Задача 3 Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении р=105 Па и температуре17 0С. Как изменятся найденные величины в результате двукратного увеличения объема газа: 1) при постоянном давлении; 2) при постоянной температуре? Эффективный диаметр молекул азота d=3,7×10-8см.
| p = 10-3Па T = 300К V2 = 2V1 1) p – const 2) T – const d = 3,7×10-10 м | Решение
Средняя длина свободного пробега и коэффициенты переноса могут быть рассчитаны по следующим формулам:
 ; (1) ; (1)
 ; (2) ; (2)
 , (3)
где n – концентрация молекул газа;
<u> - средняя скорость молекулы;
m0 – масса одной молекулы; , (3)
где n – концентрация молекул газа;
<u> - средняя скорость молекулы;
m0 – масса одной молекулы;
|
| l - ? D - ? h - ? |
Концентрацию молекул можно определить из уравнения p=nkT:
n=p/kT подставим в уравнение (1):
 6,5×10-8 м.
6,5×10-8 м.
Средняя скорость <u>=  =470 м/с;
=470 м/с;
Тогда D=1×10-5 м2/с.
Для расчета h подставим (1) в (3):
 1,2×10-5
1,2×10-5  .
.
Как видно из выражения (1), длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объема концентрация уменьшится вдвое. Следовательно, при любом процессе l2/l1=2.
В выражение для коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Тогда:

При р=const объем прямо пропорционален температуре: Т2/Т1=V2/V1=2, тогда D2/D1=  .
.
При Т=const D2/D1=l2/l1=2.
Вязкость зависит от скорости молекул, следовательно, и от температуры, т.е.
 ,
,
при р=const 
 ;
;
при Т=const  .
.
Ответ: l=6,5×10-8 м; D=1×10-5 м2/с; h=1,2×10-5  .
.
Задача 4 Пылинки массой 10-18 г. взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура воздуха во всем объеме одинакова: Т=300 К.
m1 = 10-21 кг
T = 300 К

| Решение При равновесном распределении пылинок их концентрация зависит только от координаты z по оси, направленной вертикально. По распределению Больцмана: n=n0×e-u/kT=n0×e-mgz/kT. (1) |
| DZ - ? |
Дифференцируя выражение (1) по z, получим
dn=-n0×  ×e-mgz/kT×dz.
×e-mgz/kT×dz.
Так как n0×e-mgz/kT=n, то dn=-  ×n×dz. Отсюда dz=
×n×dz. Отсюда dz=  .
.
Знак «-» показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0). Знак «-» опускаем и заменяем dz и dn конечными приращениями Dz и Dn:
 .
.
Dn/n=0,01 по условию задачи. Подставляя значения, получим Dz=4,23 мм.
Ответ: Dz=4,23 мм
Задача 5 Вычислить удельные теплоемкости сv и сp смеси неона и водорода. Массовые доли газов w1=0,8 и w2=0,2. Значения удельных теплоемкостей газов – неон: сv=6,24  ; cp=1,04
; cp=1,04  ; водород: сv=10,4
; водород: сv=10,4  ; сp=14,6
; сp=14,6  .
.
| w1 = 0,8 w2 = 0,2 cV1 = 6,24 кДж/кг × К cp1 = 1,04 кДж/кг × К cV2 = 10,4 кДж/кг × К cp2 = 14,6 кДж/кг × К | Решение
Теплоту, необходимую для нагревания смеси на DТ, выразим двумя соотношениями:
 , (1)
где сv – удельная теплоемкость смеси,
m1 – масса неона,
m2 – масса водорода,
и , (1)
где сv – удельная теплоемкость смеси,
m1 – масса неона,
m2 – масса водорода,
и  , (2)
где cv1 и сv2 – удельные теплоемкости неона и водорода соответственно. , (2)
где cv1 и сv2 – удельные теплоемкости неона и водорода соответственно.
|
| cp - ? cv - ? | Приравняв правые части выражений (1) и (2) и разделив обе части полученного равенства на DТ, найдем: |
 ,
,
откуда  .
.
Отношения  и
и  выражают массовые доли неона и водорода соответственно. С учетом этих обозначений последняя формула примет вид:
выражают массовые доли неона и водорода соответственно. С учетом этих обозначений последняя формула примет вид:
 ,
,
Подставляя значения, получим сv=2,58×103 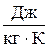 .
.
Таким же образом получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

Подставляя значения, получим ср=3,73103 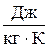 .
.
Ответ: сv=2,58×103 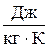 ; ср=3,73103
; ср=3,73103 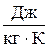 .
.
Дата добавления: 2015-01-01; просмотров: 238; Мы поможем в написании вашей работы!; Нарушение авторских прав |