V 1: Суждение как форма мышления

I:

S: Суждение можно охарактеризовать как

- : мысль о предмете со стороны его существенных признаков,

- : языковое выражение мысли, которое может ассоциироваться с различным содержанием

- : это обобщение и выделение, описание какой-либо мысли

+ : единица мышления, содержащая некоторое утверждение или отрицание и обладающее вследствие этого определенным значением истинности

I:

S: Атрибутивное суждение выражается схемой

- : А В

+ : S – Р

- : А = В

- : S = P

I:

S: Схема частноотрицательного суждения

- : Все S есть P

- : Ни одно S не есть P

+ : Некоторые S не есть P

- : Некоторые S есть Р

I:

S: Коньюнктивные суждения символически выражаются

+ : p Λ q

- : p V q

- : p→q

- : p 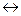q

I:

S: Виды сложных суждений

+ : соединительные (конъюнктивные)

- : отрицательные

- : положительные

+ : разделительные (дизъюнктивные)

+ : условные (импликативные)

+ : эквивалентные

I:

S: Схема общеотрицательного суждения

- : Все S есть P

+: Ни одно S не есть P

- : Некоторые S не есть P

- : Некоторые S есть Р

I:

S: Отношения контрарности в логическом квадрате выражаются

+ : А¾Е A E

- : I¾O

- : A¾I, E¾O

- : A¾O, E¾I

I O

I:

S: Импликативные суждения символически выражаются

- : p Λ q

- : p V q

+: p→q

- : p 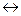q

I:

S: Отношения подчинения в логическом квадрате выражаются

- : А¾Е A E

- : I¾O

+: A¾I, E¾O

- : A¾O, E¾I

I O

I:

S: В категорическом силлогизме средний термин используется

+: большей и меньшей посылках

- : в заключении

- : в заключении и меньшей посылке

- : только в заключении

I:

S: Схема частноутвердительного суждения

- : Все S есть P

- : Ни одно S не есть P

- : Некоторые S не есть P

+: Некоторые S есть Р

I:

S: Дизъюнктивные суждения символически выражаются

- : p Λ q

+: p V q

- : p→q

- : p 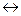q

I:

S: Отношения контрадикторности в логическом квадрате выражаются

- : А¾Е A E

- : I¾O

- : A¾I, E¾O

+: A¾O, E¾I

I O

I:

S: Соединительное суждение «Преступление – это общественно опасное и противоправное деяние» выражается как

- : два субъекта и один предикат

+: один субъект и два предиката

- : два субъекта и два предиката

- : один субъект и один предикат

I:

S: Простые суждения бывают

+ : атрибутивными

- : определенными

- : неопределенными

+ : суждения об отношениях (реляционные)

I:

S: Схема общеотрицательного суждения

- : Все S есть P

+: Ни одно S не есть P

- : Некоторые S не есть P

- : Некоторые S есть Р

I:

S: Эквивалентные суждения символически выражаются:

- : p Λ q

- : p V q

- : p→q

+: p 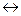q

I:

S: Отношения субконтрарности в логическом квадрате выражаются:

- : А¾Е A E

+: I¾O

- : A¾I, E¾O

- : A¾O, E¾I

I O

I:

S: По качеству атрибутивные суждения бывают

+: утвердительные

- : генетические

- : регистрирующие

+ : отрицательные

I:

S: По количеству атрибутивные суждения бывают

+ : единичные

+ : частные

- : множественные

+ : общие

I:

S: Суждение «Часть преступлений относится к экономическим» является

+ : атрибутивным

+ : частным

- : общим

- : реляционным

- : единичным

I:

S: Модальность суждений

+ : эпистемическая

- : эквивалентная

+ : деонтическая

+ : алетическая

I:

S: Схема частноотрицательного суждения:

- : Все S есть P

- : Ни одно S не есть P

+: Некоторые S не есть P

- : Некоторые S есть Р

I:

S: Отношения эквивалентности в логическом квадрате

- : А¾Е A E

- : I¾O

+: не выражаются

- : A¾I, E¾O

- : A¾O, E¾I

I O

I:

S: Атрибутивные суждения делятся на четыре группы

+ : общеутвердительные

+ : общеотрицательные

- : неопределенные

+ : частноутвердительные

+ : частноотрицательные

- : конкретные

I:

S: Правильная последовательность символических обозначений суждений и их формул

А : Все S суть P

Е : Ни одно S не есть P

I : Некоторые S есть P

О : Некоторые S не есть P

I:

S: Суждение, которое раскрывает признаки предмета называется ###

+ : атрибутивным

+ : ат*иб*ти*ным

+ : ат*иб*ти#$#

I:

S: Соответствие между видами сложных суждений и их символическим обозначением

1: конъюнкция

2: дизъюнкция

3: импликация

4: эквиваленция

1: p Λ q

2: p V q

3: p→q

4: p 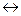q