
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частина третя
3.1.  ; 0< х2 + 4х ≥ (0,2)-1; 0<х2 + 4х ≥ 5. Маємо систему рівнянь
; 0< х2 + 4х ≥ (0,2)-1; 0<х2 + 4х ≥ 5. Маємо систему рівнянь 

ВАРІАНТ 12
Частина прерша 
| А | Б | В | Г | |
| 1.5 | Х | |||
| 1.6 | Х | |||
| 1.7 | Х | |||
| 1.8 | Х |
| А | Б | В | Г | |
| 1.9 | Х | |||
| 1.10 | Х | |||
| 1.11 | Х | |||
| 1.12 | Х |
| А | Б | В | Г | |
| 1.1 | Х | |||
| 1.2 | Х | |||
| 1.3 | Х | |||
| 1.4 | Х |
1.1.  Відповідь А.
Відповідь А.
1.4.  Максимальна кількість костюмів — 5 Відповідь В.
Максимальна кількість костюмів — 5 Відповідь В.
1.6.  Відповідь Б.
Відповідь Б.
1.7.  Відповідь Г.
Відповідь Г.
1.8.  Відповідь В.
Відповідь В.
1.9.  Відповідь В.
Відповідь В.
1.10. 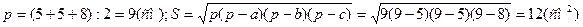
Відповідь Б.
1.11.  Відповідь Б.
Відповідь Б.
1.12. Нехай  тоді оскільки трикутники рівні, то
тоді оскільки трикутники рівні, то 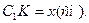
З  Відповідь А.
Відповідь А.
Частина друга

|
|



 2.1.
2.1.  Як бачимо, при
Як бачимо, при  функція набуває мінімального значення
функція набуває мінімального значення  а при
а при  функція набуває максимального значення
функція набуває максимального значення 
 Відповідь -1;7.
Відповідь -1;7.
2.2. ОДЗ:  —
—
Не входить в ОДЗ,  Відповідь 6.
Відповідь 6.
2.3. Первісна для даної функції має вигляд: 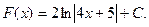
Знайдемо  Остаточно маємо:
Остаточно маємо:
 Відповідь
Відповідь 
2.4. У  Нехай
Нехай 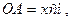 тоді
тоді  За теоремою Піфагора, маємо:
За теоремою Піфагора, маємо: 
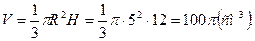 .
.
Відповідь 
Частина третя
3.1. 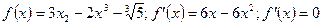 , коли
, коли  Зміну знаків похідної дано на рисунку.
Зміну знаків похідної дано на рисунку.
Отже, 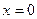 — точка мінімуму,
— точка мінімуму,  — точка максимуму.
— точка максимуму.
Відповідь. 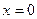 — точка мінімуму,
— точка мінімуму,  — точка максимуму.
— точка максимуму.
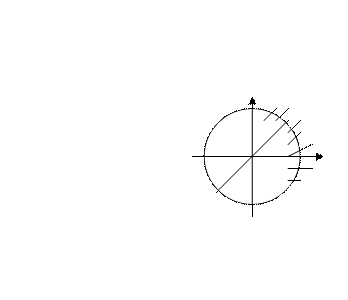 3.2.
3.2. 
 , тоді
, тоді  y
y
Маємо 


Враховуючи, що 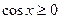 , маємо
, маємо 
 , тоді
, тоді 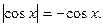
Маємо 
 Це рівняння не має розв’язків, що задоволняють умову
Це рівняння не має розв’язків, що задоволняють умову 
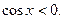

Враховуючи, що  , маємо
, маємо 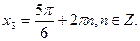
Відповідь. 
3.3. Нехай піраміда QABCD така, що ABCD — квадрат і QDC  ABC та QDA
ABC та QDA  ABC. Звідси отримуємо, що QD
ABC. Звідси отримуємо, що QD  ABC, а томубічне ребро QD є також висотою піраміди, а точка D — основої цієї висоти.
ABC, а томубічне ребро QD є також висотою піраміди, а точка D — основої цієї висоти.
З бічних ребер піраміди найбільшими є те, яке має найбільшу проекцію, тобто ребро QB. За умовою.  .
.
Нехай DK — відстан0ь від точки D до середини ребра QB. За умовою, DK=d. Оскільки DK — мередіана прямокутного трикутника, що проведена до гіпотенузи, то QВ = 2d.
У 
АBCD — квадрат, нехай DC = BC = x, тоді 
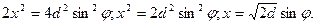
Відповідь. 

ВАРІАНТ 13
Частина перша
| А | Б | В | Г | |
| 1.5 | Х | |||
| 1.6 | Х | |||
| 1.7 | Х | |||
| 1.8 | Х |
| А | Б | В | Г | |
| 1.9 | Х | |||
| 1.10 | Х | |||
| 1.11 | Х | |||
| 1.12 | Х |
| А | Б | В | Г | |
| 1.1 | Х | |||
| 1.2 | Х | |||
| 1.3 | Х | |||
| 1.4 | Х |
1.4 х+3>2x-7; х<10 Відповідь Г.
1.7 F´(x) = (3-cosx)´= sinx Відповідь A.
1.8 f (x) = 3x2-12. 3x-12 = 0; х2 = 4; х = 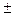 2
2
Отже, функція спадає на проміжку х  [-2;2] Відповідь Г.
[-2;2] Відповідь Г.
1.9  Відповідь Г.
Відповідь Г.
1.10 ВС = АВ 
 = 9 (см) Відповідь Б.
= 9 (см) Відповідь Б.
1.11 S =  (cм2) Відповідь А.
(cм2) Відповідь А.
1.12  . Тому
. Тому  . Відповідь В.
. Відповідь В.
Частина друга
2.1 Нехай шукані числа х і у. Тобто х < log 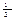 11 < у. Перетворимо дану нерівність, врахувавши що
11 < у. Перетворимо дану нерівність, врахувавши що  < 1.
< 1. 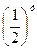 <
< 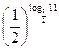 <
<  . Або 2-у < 11<2-х . Дану нерівність задовольняють числа х = -4, у = -3. Відповідь. -4; -3.
. Або 2-у < 11<2-х . Дану нерівність задовольняють числа х = -4, у = -3. Відповідь. -4; -3.
2.2 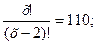 х>0 : х(х-1) = 110; х2 – х – 110 = 0; х
х>0 : х(х-1) = 110; х2 – х – 110 = 0; х  = 11, х
= 11, х 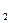 = 10 – не є корнем.
= 10 – не є корнем.
Відповідь. 11.
2.3 
 S =
S = 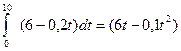



 = 6
= 6 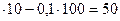 (м).
(м).
Відповідь 50 м
2.4 SABC – правильна трикутна піраміда, SO - висота, апофема бічної грані SAB; Н – середина SO; L – середина SM; HL = 2 см.  У
У  : HL – середня лінія, OM = 2 HL = 4 cм.
: HL – середня лінія, OM = 2 HL = 4 cм.  . Тому SO = OM= 4 см. OM – радіус кола, вписаного у правильний
. Тому SO = OM= 4 см. OM – радіус кола, вписаного у правильний 
 (см).
(см).
S  =
= 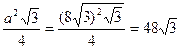 (cм2). V =
(cм2). V = 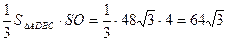 (cм2) .
(cм2) .
Відповідь  (cм2)
(cм2)
Частина третя
3.1 2log  (-х)> log
(-х)> log  (10-9 х).
(10-9 х).
ОДЗ нерівності визначимо із системи: 
 , тобто х<0.
, тобто х<0.


Далі маємо log 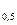 (-x)2 >log
(-x)2 >log 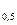 (10-9); х2 <10-9х; х2 +9х-10<0.
(10-9); х2 <10-9х; х2 +9х-10<0.
Дана нерівність виконується при -10 <х<1 (див.рисунок). Враховуючи ОДЗ, остаточно отримаємо (-10;0).
Відповідь (-10;0)
3.2 cos2х+  .
.
1) cosх 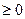 , тоді
, тоді 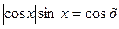 ; cosх
; cosх  .
.
а) cosх = 0; х  =
= 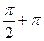 k,
k,  ;
;
б) cosх + 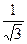 sinх =
sinх = 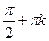 , tgх =
, tgх = 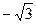 ; х = -
; х = -  , l
, l  Z. Враховуючи, що cosх
Z. Враховуючи, що cosх 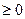 , маємо
, маємо
х2 =  , m
, m  Z.
Z.
2) cosх < 0, тоді 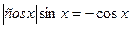 ; cosх
; cosх  .
.
а) cosх = 0. Це рівняння не має розв’язків, що задовольняють умову cosх < 0.
б) cosх  ; tgх =
; tgх =  ; х =
; х =  , l
, l  Z. Враховуючи, що cosх < 0, маємо х3 =
Z. Враховуючи, що cosх < 0, маємо х3 =  , n
, n  Z.
Z.
Відповідь: 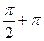 k, k
k, k  Z.
Z.
3.3 Нехай ABCDA1B1C1D1 – призма, що задана в умові; ABCD – ромб; AC > BD. У призмі проведено переріз AB1C; S 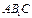 = 36 см2,
= 36 см2, 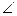 AB1C = 60
AB1C = 60  Оскільки
Оскільки  є ортогональною проекцією
є ортогональною проекцією  на площину основи, то S
на площину основи, то S 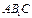 = S
= S 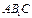
 , де
, де  - кут між площинами перерізу та основи. Отже, S
- кут між площинами перерізу та основи. Отже, S 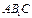 =
= 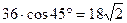 (см2).
(см2).
Тоді S 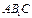
 (см2). BO
(см2). BO  AC, тоді, за теоремою про три перпендикуляри, B1O
AC, тоді, за теоремою про три перпендикуляри, B1O  AC, тому BOB1
AC, тому BOB1  AC і
AC і 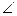 BOB1 – кут між площинами перерізу і нижньої основи.
BOB1 – кут між площинами перерізу і нижньої основи.
За умовою 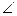 BOB1 =
BOB1 =  .
.  (за двома катетами), тому АВ = В1С і
(за двома катетами), тому АВ = В1С і  - рівнобедрений.
- рівнобедрений.
Оскільки 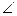 AB1C =
AB1C =  , то
, то 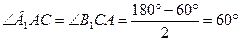 ,
,  - рівносторонній. Позначимо
- рівносторонній. Позначимо  , тоді
, тоді  ;
;  ;
; 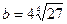 . У
. У  :
:  . У
. У  :
:  (см). Тоді об’єм призми
(см). Тоді об’єм призми 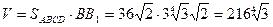 .
.
Відповідь: 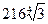 см3.
см3.
Варіант 14
Частина перша
| а | б | в | г | а | б | в | г | а | б | в | г | |||||
| 1,1 | X | 1,5 | 1,9 | |||||||||||||
| 1,2 | 1,6 | 1,10 | ||||||||||||||
| 1,3 | 1,7 | 1,11 | ||||||||||||||
| 1,4 | 1,8 | 1,12 |
Дата добавления: 2015-01-05; просмотров: 327; Мы поможем в написании вашей работы!; Нарушение авторских прав |