Задача №8

Рассматривается рынок одного товара; время считается непрерывным.

Пусть d(t), s(t), p(t), - соответственно спрос, предложение и цена этого товара в момент t.И спрос и предложение считаются линейными функциями цены: 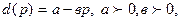т.е. спрос с ростом цены падает,

s(р)=α+βρ, α<0, β>0, т.е. предложение с ростом цены растёт.

Естественно считать, что а >0, т.е. при нулевой цене спрос имеется (иначе говоря, товар желателен).

Основное предположение состоит в том, что цена изменяется в зависимости от соотношений между спросом и предложением:

Δp-γ(d­s)Δt, где γ>0, т.е. увеличение цены прямо пропорционально превышению спроса над предложением и длительности этого превышения. Итак, получаем дифференциальное уравнение: .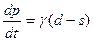

Подставляя в это уравнение линейные зависимости спроса и предложения от цены, получаем линейное неоднородное дифференциальное уравнение с начальным условием.

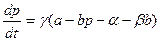; , p(0)=p₀ (1)

Уравнение (1) имеет стационарную точку 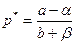, p^*>0.

Видно, что 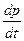>0 при p^*> p и 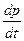<0 при p^*< p .

Отсюда следует, что lim p(t)=p^*.

t→∞

В этом случае при p^*< p цена стремится к p^* возрастая, а

при p^*> p цена стремится к p^* убывая.

Сама цена p^* есть равновесная цена (спрос равен предложению):

d(p)=s(p) => a-bp=α+βρ => .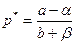

Обычный метод решения уравнения (1) - метод вариации постоянной.

Согласно этому методу общее решение есть сумма общего решения соответствующего однородного уравнения и какого - нибудь частного решения неоднородного уравнения (1).

Решение дифференциального уравнения (1) с начальным условием имеет вид:

p(t)= p₀ e^{-γ(b+β) t} + ( 1-e^{-γ(b+β) t} ) или p(t)= p₀ e^{-γ(b+β) t} + p^* ( 1-e^{-γ(b+β) t} ).

Вариант 1.q ₀=8, q ₁=2, s ₀=-6, s ₁=2, p(0)=p₀ =1,5, k=0,5

Вариант 2.q ₀=10, q ₁=3, s ₀=-4, s ₁=3, p(0)=p₀ =2,5, k=0,5

Вариант 3.q ₀=12, q ₁=6, s ₀=-2, s ₁=4, p(0)=p₀ =2, k=0,5

Вариант 4.q ₀=9, q ₁=4, s ₀=-5, s ₁=3, p(0)=p₀ =1,5, k=0,5

Вариант 5.q ₀=8, q ₁=2, s ₀=-1, s ₁=1, p(0)=p₀ =2,5, k=0,5

Вариант 6.q ₀=9, q ₁=3, s ₀=-1, s ₁=2, p(0)=p₀ =1,5, k=0,5

Вариант 7.q ₀=7, q ₁=2, s ₀=-5, s ₁=1, p(0)=p₀ =3,5, k=0,5

Вариант 8.q ₀=5, q ₁=1, s ₀=-1, s ₁=2, p(0)=p₀ =1,5, k=0,5

Вариант 9.q ₀=9, q ₁=2, s ₀=-2, s ₁=3, p(0)=p₀ =2, k=0,5

Вариант 10.q ₀=11, q ₁=3, s ₀=-1, s ₁=3, p(0)=p₀ =1,5, k=0,5

Вариант 11.q ₀=6, q ₁=1, s ₀=-2, s ₁=3, p(0)=p₀ =1,5, k=0,5

Вариант 12.q ₀=9, q ₁=3, s ₀=-2, s ₁=2, p(0)=p₀ =2, k=0,5

Вариант 13.q ₀=15, q ₁=2, s ₀=-3, s ₁=4, p(0)=p₀ =2,5, k=0,5

Вариант 14.q ₀=13, q ₁=5, s ₀=-1, s ₁=2, p(0)=p₀ =1,5, k=0,5

Вариант 15.q ₀=8, q ₁=1, s ₀=-1, s ₁=2, p(0)=p₀ =2,5, k=0,5

Вариант 16.q ₀=14, q ₁=3, s ₀=-2, s ₁=5, p(0)=p₀ =1,5, k=0,5

Вариант 17.q ₀=10, q ₁=2, s ₀=-2, s ₁=2, p(0)=p₀ =2,5, k=0,5

Вариант 18.q ₀=15, q ₁=3, s ₀=-1, s ₁=5, p(0)=p₀ =1,5, k=0,5

Вариант 19.q ₀=16, q ₁=5, s ₀=-2, s ₁=4, p(0)=p₀ =1,5, k=0,5

Вариант 20.q ₀=13, q ₁=2, s ₀=-2, s ₁=3, p(0)=p₀ =2,5, k=0,5