
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. 1) Вычисляем коэффициенты прямых затрат aij, показывающие, какой объем продукции i-ой отрасли идет на производство одной единицы продукции j-ой отрасли:
1) Вычисляем коэффициенты прямых затрат aij, показывающие, какой объем продукции i-ой отрасли идет на производство одной единицы продукции j-ой отрасли:

2) Выписываем столбец валового выпуска X, столбец нового конечного выпуска Y, а также матрицу прямых затрат А.
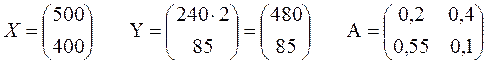
3) Вычисляем матрицу E-A

4) Вычисляем матрицу полных затрат S=(E-A)-1. Каждый элемент sij этой матрицы показывает величину валового выпуска i-ой отрасли, необходимого для обеспечения выпуска одной единицы конечного продукта j-ой отрасли.
4.1. Вычисляем определитель 
4.2. Находим транспонированную матрицу 
4.3. Строим присоединенную матрицу:


4.4. Находим обратную матрицу: 
5) Вычисляем новый вектор валового выпуска:

6) Строим новую балансовую таблицу, предварительно вычисляя недостающие величины:

| № | Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
| 5. | Энергетическая | 186,4 | 265,6 | |||
| 6. | Машиностроение | 512,6 | 66,4 |
Проверка: 
Задача № 4
В результате маркетингового исследования установлено, что функции спроса и предложения имеют вид:
1.  - спроса, - спроса,
|  - предложения, - предложения,
|
где p – цена товара.
Найти:
1) Равновесную цену p0.
2) Эластичность спроса и предложения для этой цены.
3) Изменение дохода при увеличении цены на 5% от равновесной.
Решение
1) Определяем равновесную цену p0, при которой спрос равен предложению.

Отсюда p0=2. (Отрицательный корень отбрасываем, как не имеющий экономического смысла).
График зависимостей спроса и предложения от цены представлен на рис. 1.
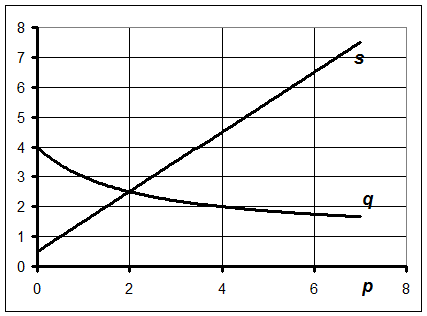
Рис.1. Зависимости спроса и предложения от цены.
2) Находим эластичности спроса и предложения для равновесной цены.
2.1. Находим производные q’(p) и s’(p).


2.2. Получаем общие выражения для эластичностей спроса и предложения.


2.3. Вычисляем эластичности спроса и предложения при равновесной цене.
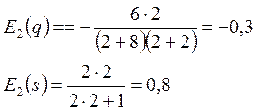
Таким образом, при увеличении цены на 1% от равновесного значения спрос уменьшается (т.к. «-») на 0, 3%, а предложение возрастает (т.к. «+») на 0,8%.
3) Выведем общее выражение для эластичности дохода R=pq по цене, пользуясь свойствами эластичности и подставим в него численные значения p0 и E2(q):
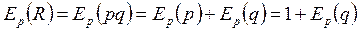

Это означает, что при увеличении цены на 1% от равновесного значения доход увеличивается на 0,7%. Следовательно, при увеличении цены на 5% от ее равновесного значения доход увеличится на 5×0,7%=3,5%.
Ответ:1) равновесная цена товара равна 2; 2) при увеличении цены на 1% от равновесного значения спрос уменьшается на 0, 3%, а предложение возрастает на 0,8%; 3) при увеличении цены на 5% от ее равновесного значения доход увеличится на 3,5%.
Дата добавления: 2015-01-05; просмотров: 319; Мы поможем в написании вашей работы!; Нарушение авторских прав |