Задача №8. Нахождение общего решения дифференциального уравнения, раскрывающего зависимость спроса и предложения товара от цены.

Нахождение общего решения дифференциального уравнения, раскрывающего зависимость спроса и предложения товара от цены.

1. Q(p)= q₀ – q₁p(t) - зависимость спроса от цены

S(p)= s₀ – s₁ p(t) - зависимость предложения от цены

q₀ =10, q₁ =2, Q(p)= 10-2p(t)

s₀ = -4, s₁=4, S(p)=-4+4p(t)

Начальная цена: p(0)= p₀=2

Дифференциальное уравнение зависимости цены от времени:

2. к(Q(p(t))- S(p(t)) ) (1), к=0,5

Подставляя численные данные, получаем:

(10-2р+4-4р),

(14-6р),

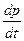=7-3р; 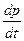-7+3р=0. (2).

Начальные условия p(0)=2 (3).

Имеем задачу линейного неоднородного дифференциального уравнения Коши для первого порядка.

3. Найдём решение (2) в виде:

р=uv; р´=u´v+ u v´, т.е. ; (4)

Подставляем (4) в (2)

+3 uv-7=0;

-7=0

4. Полагаем , тогда

5. Решаем (5) =-3и; ; ;

, ln│u│=-3t+ln C.

Полагаем, что С=1, тогда ln 1=0 и ln│u│=-3t, и=е^{- 3 t} (7)

6. Подставляя (7) в (6) получим е^{- 3 t} -7=0; => е^{- 3 t} =7;

=7 е ^{3 t} ; => , проинтегрируем обе части уравнения,

, получим v=7* e^3t+C или v= e^3t+C (8)

7. Подставляя (7) и (8) в р=uv, получаем:

р= е^{- 3 t} ( e^3t+C), р= е^{- 3 t} e^{3 t} + С е^{- 3 t},

р= е⁰ + С е^{- 3 t}, р= + С е^{- 3 t}

Найдём С, используя начальное условие p(0)=2 .

2 = + С е⁰, 2- =С; - =С.

p(t)= - е^{- 3 t}_.

8. Найдём равновесную цену р^*:

Q(p^*) = S(p^*); 10-2р^*=-4+4 р^*; 14=6р^*, р^*=2 .

Решение можно записать в виде

p(t)= р^* - е^{- 3 t} (*)

Примечание р₀ - р^*=2- = - ,

Следовательно (*) имеет вид:

p(t)= р^*+ (р₀ - р^*) е^{- 3 t}_.