
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Учитывая, что прибыль представляет собой разность между доходом и издержками, и подставляя численные данные
Учитывая, что прибыль представляет собой разность между доходом и издержками, и подставляя численные данные, получаем явный вид зависимости прибыли от объема производства:
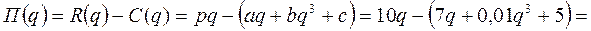

1) Выполняем полное исследование функции П(q)
1.1. Область определения D(П)=[0;+∞].
1.2. Находим первую и вторую производную П’(q) и П’’(q)


1.3. Находим критические точки, решая уравнение П’(q)=0
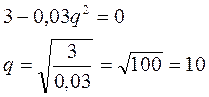
1.4. Наносим критическую точку на числовую ось, и находим знак первой производной на каждом из получившихся интервалов:

Из рисунка делаем выводы о том, что функция возрастает при 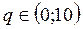 , а убывает при
, а убывает при  ; в точке q=10 функция имеет максимум.
; в точке q=10 функция имеет максимум.
Вычислим значение функции в этой точке:

1.5. Найдем точку перегиба графика функции, решая уравнение П’’(q)=0

Так как случай q=0 не представляет практического интереса, будем считать, что график функции точек перегиба не имеет.
1.6. Найдем, на каких интервалах график функции выпуклый, а на каких—вогнутый.
Так как  на всей области определения, делаем вывод о том, что график функции выпуклый на всей области определения.
на всей области определения, делаем вывод о том, что график функции выпуклый на всей области определения.
1.7. Сводим все полученные результаты в итоговую таблицу:
Таблица 1.
| q | П’(q) | П’’(q) | П(q) | Примечания |
| 0 | + | — | -5 | график выпуклый |
| (0;10) | + | — | ↑ | график выпуклый |
| 10 | 0 | — | 15 | максимум |
| (10;+∞) | — | — | ↓ | график выпуклый |
1.8. Строим схематический график функции
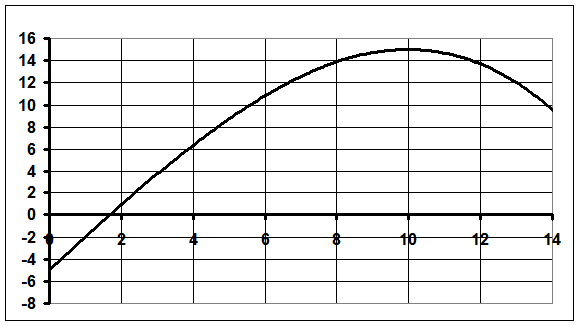
Рис.2. График зависимости прибыли от объема выпуска продукции.
2) Очевидно, что оптимальным для фирмы является объем выпуска, равный 10, при этом прибыль будет максимальна и составит 15.
Ответ в данной задаче нет необходимости выписывать отдельно, так как он фактически содержится в таблице 1.
Дата добавления: 2015-01-05; просмотров: 253; Мы поможем в написании вашей работы!; Нарушение авторских прав |