Решение. Прежде всего установим экономический смысл параметров α и β

Прежде всего установим экономический смысл параметров α и β. Для этого найдем частные эластичности выпуска по основным фондам и трудовым ресурсам.

Находим и :

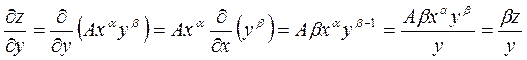
Находим частные эластичности выпуска продукции по основным фондам и трудовым ресурсам:

Таким образом, параметр α показывает, на сколько процентов изменяется выпуск продукции при увеличении объема основных фондов на 1%. Аналогично, параметр β показывает, на сколько процентов изменяется выпуск продукции при увеличении объема трудовых ресурсов предприятия на 1%.

После этих вводных замечаний приступаем к решению задачи.

1) Определим явный вид производственной функции.

1.1. Учитывая экономический смысл параметров α и β, получаем:

,

Производственная функция принимает вид: (1)

1.2. Определяем параметр A.

Для этого подставляем в выражение (1) известные величины M=10⁴, L=10³, K=10⁸ и учитывая, что в настоящее время выпуск продукции равен , получаем следующее уравнение для определения A:

, откуда A=100.

Таким образом, производственная функция данной фирмы имеет вид:

(2)

2) Определим оптимальный размер фирмы.

В качестве критерия оптимизации выбираем прибыль, т.е. оптимальным будем считать такой размер фирмы, при котором ее прибыль максимальна.

Выражение для прибыли (разность между доходами и издержками) имеет вид:

, (3)

где:

p₁-себестоимость одной единицы основных фондов,

p₂-себестоимость одной единицы трудовых ресурсов.

По условию задачи

Таким образом, задача свелась к нахождению максимума функции двух переменных:

, (4)

который находится по общим правилам дифференциального исчисления.

2.1. Находим все частные производные функции (4) первого и второго порядка:

2.2. Находим критические точки функции, приравнивая первые частные производные к нулю и решая получившуюся систему уравнений:

Выражаем из первого уравнения и подставляем во второе. Получаем:

Отсюда

Поставляя найденное значение y в первое уравнение, находим x:

Итак, точка 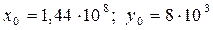является критической точкой функции прибыли данной задачи.

Однако равенство нулю частных производных первого порядка является необходимым, но совсем не достаточным условием экстремума функции двух переменных. Для ответа на этот вопрос следует воспользоваться достаточным признаком экстремума, что и будет сделано в следующем пункте.

2.3. Вычисляем значения вторых производных в критической точке:

Вычисляем определитель:

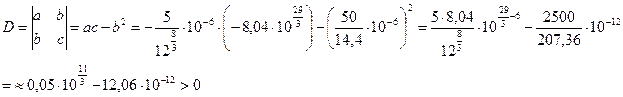Поскольку a<0, D>0, то на основании достаточного признака экстремума функции двух переменных делаем вывод о том, что точка является точкой максимума функции прибыли. Следовательно, это и есть оптимальный размер фирмы.

2.4. Вычислим оптимальный объем выпуска продукции z₀ и оптимальную прибыль

Ответ:оптимальными для данной фирмы являются: объем основных фондов 1,44×10⁸ руб, численность работников 8×10³ чел. При этом прибыль будет максимальна и составит 4×10⁶ руб при объеме выпуска продукции, равном 2,4×10⁷ руб