IV. Решение примеров и задач действием деления.

Пропедевтика темы «Деление с остатком».

1. Практическая работа.

Учитель предлагает учащимся с помощью фигурок наборного полотна выполнить деление, записать и решить выражения.

Н а п р и м е р: учитель выставляет на наборное полотно 12 яблок.

– Как можно 12 яблок разделить между 3 детьми поровну? (Один из учащихся выполняет работу у доски.)

– Как записать то, что вы сейчас выполнили?

– Запись с комментированием:

12: 3 = 4

– Как можно 12 яблок разделить между 4 детьми поровну?

– Запишите то, что выполняли.

Запись с комментированием.

12 : 4 = 3

– Как можно 12 яблок разделить между 2 (6) детьми поровну?

– Запишите это.

Запись с комментированием:

12 : 2 = 6

12 : 6 = 2

Аналогичная работа проводится по рисункам с. 51 учебника (часть 2, задание 1).

2. Работа с учебником.

К задаче 2 (с. 51 учебника, часть 2) учащиеся выполняют рисунок и записывают решение задачи действием деления. (Один учащийся выполняет работу на доске с использованием фигурок наборного полотна.)

Работа над задачей 3 (с. 51 учебника, часть 2) является пропедевтической работой к изучению темы «Деление с остатком».

Работу можно построить следующим образом: после того как учащиеся прочитали задачу, учитель беседует с ними.

– Сколько дощечек идет на один скворечник? (Семь.)

– Сколько дощечек имеется? (Пятнадцать.)

– Можно из пятнадцати дощечек сделать один скворечник?

– Докажите это. (Если из пятнадцати дощечек взять семь на изготовление скворечника, то восемь дощечек останется.)

– Можно ли из пятнадцати дощечек сделать два скворечника?

– Как это узнать? (На один скворечник идёт 7 дощечек. Чтобы узнать, сколько дощечек идёт на 2 скворечника, надо 7 умножить на 2 или к 7 прибавить 7, получится 14. Из 15 дощечек возьмём 14 на изготовление скворечника, и 1 дощечка останется.)

– Можно ли из пятнадцати дощечек сделать три скворечника?

– Как это узнать? (На один скворечник идет 7 дощечек, а на 2 – 14. Чтобы узнать, сколько дощечек идет на 3 скворечника, надо к 14 прибавить ещё 7, получится 21. 21 больше 15, значит, 3 скворечника сделать нельзя.)

– Сколько же можно сделать скворечников из 15 дощечек? (Один, два.)

При работе над задачей 4 (с. 51 учебника, часть 2) учитель показывает учащимся краткую запись задачи, которая решается умножением.

– Прочитайте задачу.

– Выделите условие (вопрос).

– Какие слова используем в краткой записи?

– Что известно про Ваню?

– Что известно про Нину?

З а п и с ь:

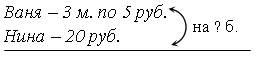
Решение задачи выполняется по действиям с объяснением.

– Можем сразу ответить на вопрос задачи?

– Почему?

– Как узнать: сколько денег у Вани?

– Запишите. (3 · 5 = 15 (руб.) у Вани.)

– Можем теперь ответить на вопрос задачи?

– Какое действие следует для этого выполнить?

– Запишите. (20 – 15 = 5 (руб.).)

– Сформулируйте ответ и запишите его.