
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двойной интеграл
Наделайте побольше таких упаковок и разложите в разные места: по карманам одежды, в сумки-чемоданы-рюкзаки, в аптечку, в ремонтный набор.
Источник: И. Николаева
http://vk.com/vnimanie_vsem
Двойной интеграл
Пусть  – замкнутая ограниченная область, а
– замкнутая ограниченная область, а 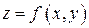 – функция, определенная и ограниченная в области
– функция, определенная и ограниченная в области  , причем граница области
, причем граница области  состоит из конечного числа кривых, заданных уравнениями вида
состоит из конечного числа кривых, заданных уравнениями вида 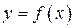 и
и  , где
, где 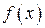 и
и  – непрерывные функции. Разобьем область
– непрерывные функции. Разобьем область  произвольными непрерывными кривыми на
произвольными непрерывными кривыми на  частей
частей  , с площадями
, с площадями 
 . На каждой части
. На каждой части  выберем произвольную точку
выберем произвольную точку  и составим сумму
и составим сумму
 , (1)
, (1)
которая называется интегральной суммой для функции  в области
в области  . Диаметром области
. Диаметром области  называется наибольшее расстояние между граничными точками этой области. Обозначим
называется наибольшее расстояние между граничными точками этой области. Обозначим  наибольший из диаметров частичных областей
наибольший из диаметров частичных областей 
 .
.
Определение. Если интегральная сумма (1) при  имеет конечный предел
имеет конечный предел  , независящий от способа разбиения области
, независящий от способа разбиения области  на части и выбора точек
на части и выбора точек  , то этот предел называется двойным интегралом функции
, то этот предел называется двойным интегралом функции  по области
по области  и обозначается
и обозначается
 .
.
В этом случае функция 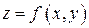 называется интегрируемой в области
называется интегрируемой в области  ,
,  – областью интегрирования,
– областью интегрирования,  – элементом площади. Известно, что
– элементом площади. Известно, что  непрерывна в области
непрерывна в области  , то
, то  существует. А если при этом для любого
существует. А если при этом для любого  , где
, где  и
и  – крайние слева и справа точки области
– крайние слева и справа точки области 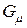 – любая прямая, параллельная оси
– любая прямая, параллельная оси  , пересекает границу области
, пересекает границу области  только в двух точках с ординатами
только в двух точках с ординатами  и
и  , где
, где  , то двойной интеграл приводится к повторному :
, то двойной интеграл приводится к повторному :
 . (2)
. (2)
Если 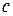 и
и 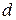 – крайние снизу и сверху точки области
– крайние снизу и сверху точки области  . а кривые
. а кривые  и
и 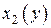 ограничивают ее слева и справа, то при аналогичных условиях
ограничивают ее слева и справа, то при аналогичных условиях
 . (3)
. (3)
Сменить пределы интегрирования – значит перевести интеграл (2) к интегралу (3) (или наоборот).
Пример 1. Изменить порядок интегрирования и вычислить интеграл
 .
.
Решение. Область  ,
, 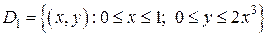 ,
, 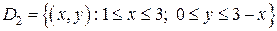 . Для лучшего рассмотрения изобразим эти области, начертив граничные линии
. Для лучшего рассмотрения изобразим эти области, начертив граничные линии  ,
,  ,
,  ,
,  для области
для области  и
и  ,
,  ,
,  ,
,  – для
– для  .
.
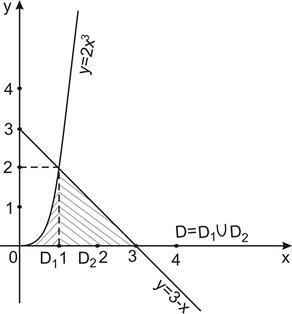
Зададим область  по другому, решив уравнения
по другому, решив уравнения  И
И  относительно переменно
относительно переменно  :
:
 и
и  ,
,
при этом  , то
, то  .
.
Получим
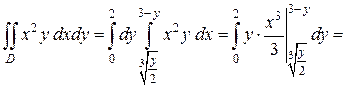
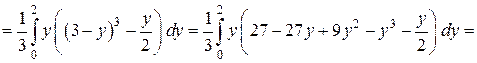
 .
.
Дата добавления: 2015-01-05; просмотров: 323; Мы поможем в написании вашей работы!; Нарушение авторских прав |