
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Криволинейный интеграл второго рода
Пусть вдоль дуги кривой  определена функция
определена функция  . Разобьем дугу
. Разобьем дугу  на
на  частей точками
частей точками  и на каждой частичной дуге
и на каждой частичной дуге  выберем по точке
выберем по точке  . Обозначим
. Обозначим 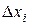 проекцию частичной дуги
проекцию частичной дуги  на ось
на ось  и составим сумму вида
и составим сумму вида
 . (10)
. (10)
которая называется интегральной.
Определение. Если интегральная сумма (10) при  (
( 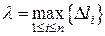 ,
,  – длина дуги
– длина дуги  ) имеет конечный предел I, который не зависит по способа разбиения дуги на части и выбора точек
) имеет конечный предел I, который не зависит по способа разбиения дуги на части и выбора точек  , то он называется криволинейным интегралом второго рода функции
, то он называется криволинейным интегралом второго рода функции  вдоль дуги
вдоль дуги  и обозначается
и обозначается
 .
.
Аналогично определяется
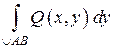 .
.
Сумму  называют общим криволинейным интегралом и обозначают
называют общим криволинейным интегралом и обозначают
 . (11)
. (11)
Вычисление интеграла (11).
Пусть функции  и
и  непрерывны на дуге
непрерывны на дуге  и кривая
и кривая  задана параметрически уравнениями
задана параметрически уравнениями  ,
,  , причем
, причем  и
и 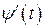 – непрерывные функциипри
– непрерывные функциипри  . Значению
. Значению 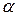 соответствует точка
соответствует точка  , значению
, значению  – точка
– точка 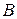 и
и  . Тогда справедлива формула
. Тогда справедлива формула
 . (12)
. (12)
В частности, если дуга  задана уравнением
задана уравнением 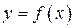 ,
,  ,
,  – непрерывна, получаем
– непрерывна, получаем
 . (13)
. (13)
Пример.
а)  ;
; 
по формуле (13);
б)  ;
;  ,
,  .
.
Удобнее перейти к параметрическому заданию контура  :
:  ,
,  ,
, 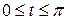 . Используем (12):
. Используем (12):
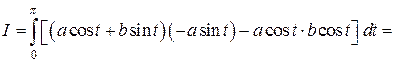

 .
.
Дата добавления: 2015-01-05; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |