
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замена переменных в двойном интеграле
Предположим, что мы переходим в двойном интеграле
 (4)
(4)
от переменных  и
и  к новым переменным
к новым переменным  и
и  , при помощи преобразований
, при помощи преобразований
 , (5)
, (5)
тогда имеет место
Теорема. Если преобразования (5), переводящие область  в область
в область  изменения переменных
изменения переменных  и
и  , являются взаимно однозначными, функции (5) имеют непрерывные частные производные первого порядка и определитель
, являются взаимно однозначными, функции (5) имеют непрерывные частные производные первого порядка и определитель
 ,
,
называемый якобианом, отличен от 0, то имеет место формула замены переменных
 . (6)
. (6)
Рассмотрим важный частный случай, когда новыми координатами точек  являются их полярные координаты, т.е. формулы преобразований (5) имеют вид
являются их полярные координаты, т.е. формулы преобразований (5) имеют вид
 . (7)
. (7)
В этом случае
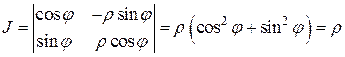
и мы, согласно (6), получим
 . (8)
. (8)
Пример 2. Найти массу пластины, ограниченной линией 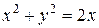 , если ее плотность в каждой точке равна абсциссе этой точки.
, если ее плотность в каждой точке равна абсциссе этой точки.
Решение.


 .
.
(Использовали рекуррентную формулу  , где
, где  или
или 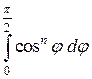 ,
,  . Например,
. Например,

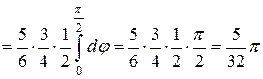 .
.
Если же в подынтегральном выражении или в уравнении, задающем область интегрирования, встречается выражение
 ,
,
то можно перейти к обобщенным полярным координатам
 . (9)
. (9)
Тогда
 ,
, 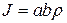 .
.
Пример 3. Найти объем тела, ограниченного поверхностями  ,
,  .
.
Решение. Проекцию этого тела на плоскость  найдем из системы уравнений
найдем из системы уравнений
 ,
,
получим 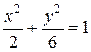 , т.е. эллипс – граница области интегрирования ё
, т.е. эллипс – граница области интегрирования ё  . Объем равен
. Объем равен  . Переходим в обобщенные полярные координаты
. Переходим в обобщенные полярные координаты  ,
,  ,
,  . Тогда
. Тогда
 ,
,
т.е. уравнение границы области  . Область
. Область  , в которую переходит область
, в которую переходит область  , задается неравенствами
, задается неравенствами  ,
,  . Эллиптический параболоид
. Эллиптический параболоид  перейдет в поверхность
перейдет в поверхность  . Тогда
. Тогда

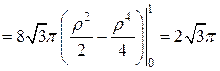 .
.
Дата добавления: 2015-01-05; просмотров: 348; Мы поможем в написании вашей работы!; Нарушение авторских прав |